关于p值的理解
数理统计———关于p值的看法与理解
-
- 问题背景
- 相关知识
- p值的产生过程
- 对于p值及$\alpha$值的一些考虑
- p值的计算
- p值的缺点及前世今生
问题背景
p值是数理统计假设检验中的一个重要概念,它的优点在于做检验(卡方检验,F检验,t检验,U检验)时不用事先确定显著性水平 α \alpha α,我们知道显著性水平是接受或拒绝原假设的“态度坚决”的一个指标。一般 α \alpha α的选择有0.1,0.05,0.01,事实上我们有无数个选择,但这显然也会带来一个问题,在某个具体问题中,选择怎样的 α \alpha α是比较合理的?遇 α \alpha α不决,p值无疑是个很好的选择。但p值也有其不足与缺陷,关于这一点我们在将在最后进行讨论。
相关知识
首先我们为即将讨论的问题铺垫好舞台, 引入两个空间(比较熟悉的请忽略)
样本空间: ( X 1 , X 2 , ⋯ , X n ) ∈ X (X_1,X_2,\cdots,X_n)\in X (X1,X2,⋯,Xn)∈X,实验中将从 X X X中抽取一定数目,形成样本 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) (x1,x2,⋯,xn)
参数空间:假设检验(不考虑非参数检验)的参数对象可能取的值的集合, ( θ 1 , θ 2 , ⋯ , θ m ) ∈ Θ (\theta_1,\theta_2,\cdots,\theta_m)\in\Theta (θ1,θ2,⋯,θm)∈Θ
规定出这两个空间之后,我们很容易得知:
零假设&备择假设:假设是对参数空间 Θ \Theta Θ的划分,不同假设对应着不同的划分
拒绝域:拒绝域是对样本空间 X X X的划分
检验统计量 T ( X 1 : n ) T(X_{1:n}) T(X1:n):本质是个统计量,也即从总体(population)抽取出样本后其值即能确定,用于对样本空间进行,形成拒绝域
简单假设检验一般分为单边检验(左侧检验、右侧检验)和双边检验,对于单边情形:
W = { ( x 1 , x 2 , ⋯ , x n ) : φ ( x 1 , x 2 , ⋯ , x n ) > λ } ( 1 ) W=\{(x_1,x_2,\cdots,x_n):\varphi(x_1,x_2,\cdots,x_n)>\lambda\} (1) W={(x1,x2,⋯,xn):φ(x1,x2,⋯,xn)>λ}(1)
(如果不等式是小于号<,可以对检验统计量乘上一个负1,形式就又回到上面(1)式) 这里的 λ \lambda λ应满足:
sup θ ∈ Θ 0 P θ ( φ ( X 1 , ⋯ , X n ) > λ α ) = α \sup_{\theta\in\Theta_0}P_{\theta}(\varphi(X_1,\cdots,X_n)>\lambda_\alpha)=\alpha θ∈Θ0supPθ(φ(X1,⋯,Xn)>λα)=α
p值的产生过程
直观含义:拒绝 H 0 H_0 H0的 α \alpha α的下确界(考虑一个参数的情形)
假设检验统计量选为 T ( X 1 : n ) T(X_{1:n}) T(X1:n) ,拒绝域取为 W : = { T ( X 1 : n ) > C } W:=\{T(X_{1:n})>C\} W:={T(X1:n)>C} 这里C是什么具体先不用理会
以下图片展示了选定一个参数 θ \theta θ( θ \theta θ来自零假设 H 0 H_0 H0),我们就能确定一个拒绝域(也即知道样本空间如何划分),进而能确定犯第一类错误的概率 α 1 \alpha_1 α1
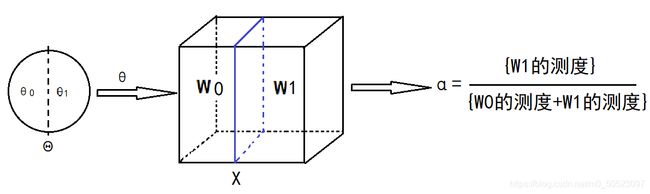
也许我们的假设并不是双边假设,这样从 H 0 H_0 H0取出来的 θ \theta θ有很多种,甚至无限种。重复上面 确 定 θ → 确 定 W 0 / W 1 → 确 定 α 确定\theta\rightarrow确定W_0/W_1\rightarrow确定\alpha 确定θ→确定W0/W1→确定α 的过程,得到 α 1 , α 2 , ⋯ \alpha_1,\alpha_2,\cdots α1,α2,⋯,其中的最小值便是p值了(以上的理解较为通俗,仅供理解)
细心的读者可能已经发现了上面的推导并不能具体把p值算出来,必须有具体的样本 x 1 : n x_{1:n} x1:n 来替换掉推导过程中的 X 1 : n X_{1:n} X1:n ,是的,因此p值可以视为依赖于样本量的函数 p ( x 1 : n ) p(x_{1:n}) p(x1:n)
但实际上p值的产生往往是基于我们常用的检验的,上面的过程或许并不显得明显
对于p值及 α \alpha α值的一些考虑
-
对于给定的 x 1 : n x_{1:n} x1:n, { α 变 大 , W α 扩 大 , 更 容 易 拒 绝 H 0 α 变 小 , W α 缩 小 , 更 容 易 接 受 H 0 \begin{cases}\alpha变大,W_{\alpha}扩大,更容易拒绝H_0\\\\\alpha变小,W_{\alpha}缩小,更容易接受H_0\end{cases} ⎩⎪⎨⎪⎧α变大,Wα扩大,更容易拒绝H0α变小,Wα缩小,更容易接受H0,这个结论可以从上面的图直观的看出来
-
对于给定的 x 1 : n x_{1:n} x1:n,如果算出其p值,而刚好这个p值和我们事先考虑的 α \alpha α值相同,该不该拒绝 H 0 H_0 H0呢?
答:一般来说,p值不会这么碰巧与我们预先定的α值相等,但如果发生这种情况,我们就要去验证说这个p值能不能取,表现在拒绝域中通常就是不等式中的符号是“大于”还是“大于等于”
-
如果给定 α , λ α \alpha,\lambda_{\alpha} α,λα 存在且唯一,可证明: T ( x 1 : n ) > λ α T(x_{1:n})>\lambda_\alpha T(x1:n)>λα 当且仅当 p ( x 1 : n ) < α p(x_{1:n})<\alpha p(x1:n)<α,具体的证明一般的数理统计课本会给,这里不再赘述
p值的计算
W α = { T ( x 1 : n ) > λ α } 满 足 P θ 0 ( T ( x 1 : n ) > λ α ) = α ⇔ W α = { T ( x 1 : n ) > F θ 0 − 1 ( 1 − α ) } W_\alpha=\{T(x_{1:n})>\lambda_\alpha\}满足P_{\theta_0}(T(x_{1:n})>\lambda_\alpha)=\alpha\Leftrightarrow W_\alpha=\{T(x_{1:n})>F^{-1}_{\theta_0}(1-\alpha)\} Wα={T(x1:n)>λα}满足Pθ0(T(x1:n)>λα)=α⇔Wα={T(x1:n)>Fθ0−1(1−α)}
设 T ( X 1 : n ) T(X_{1:n}) T(X1:n)在 θ = θ 0 \theta=\theta_0 θ=θ0下的 CDF 为 F θ 0 ( t ) F_{\theta_0}(t) Fθ0(t),因此
P ( x 1 : n ) = 1 − F θ 0 ( T ( x 1 : n ) ) = P θ 0 ( T ( X 1 : n ) > T ( x 1 : n ) ) P(x_{1:n})=1-F_{\theta_0}(T(x_{1:n}))=P_{\theta_0}(T(X_{1:n})>T(x_{1:n})) P(x1:n)=1−Fθ0(T(x1:n))=Pθ0(T(X1:n)>T(x1:n))
p值的缺点及前世今生
这里我参照了一些文章,尽是一些统计大牛,因为学识浅薄,不敢高谈阔论。就直观来说说我的感受,我觉得p值是考虑整个参数空间,要是这个参数空间性质很差,或者说,有一些极端的值,对p值是影响很大的。二是p值依赖于样本值,那要怎么这个样本的质量呢?三是其计算比较麻烦,当然,随着现代计算机的发展,这个问题基本已无伤大雅。接下来还是看看,大牛们的看法吧。
p值是由统计学界最牛的人Fisher老先生(这个人真的很牛逼!!)提出并推动的,这来源于他以及以后由奈曼和皮尔逊发展的假设检验思想。但90年前P值自诞生后就一直饱受争议,有人形容它为讨人厌又赶不走的蚊子,也有人形容为存在明显问题但人人视而不见的皇帝新衣。但实际上,1920 年英国统计学家Ronald Fisher 首次引入p值时,仅仅是想将其当做判断所得的实验数据在传统意义上是否显著的非正式方法,而非决定性的检验方法。而真正推动p值风靡全球的却是Fisher的竞争者波兰数学家Neyman及英国统计学家Pearson (这两人也是我们统计专业的老前辈了),当时他们提出另一种包含统计效能、假阳性、假阴性等概念的可替代的数据分析方法(该法直接忽视P值这个指标。至此,两个派系一直争执不下,却过早耗尽了其他研究者(非统计学家)的耐心。对两种算法均缺乏透彻理解的研究者粗略将P值融入了Neyman和Pearson 所建立的统计系统,就开创了一种新的混合统计方法——当p值<0.05,统计结果可视为显著。而目前,许多科学领域中的研究结果的意义均是由P值来判断的。它们被用来证明或驳回一个“零假设”:通常假定所测试的效果并不存在。当P值越小,该实验结果就越不可能是由纯粹的偶然所造成的。其实近年来对P值的批评一直不断,2011年一些研究者就试图对这一问题提出警告,因为有人曾利用统计学分析得出结论:大学生听披头士乐队的音乐会变得更年轻。更令人争议的是,2015年一则记录片揭露了一项基于P值的低劣临床试验是如何得出了荒谬的结果——吃巧克力可以减肥(目前该文章已被撤回)。
因而对于p值滥用的情况,2016年美国统计学会(American Statistical Association,ASA)就曾发表声明呼吁研究者们要慎用P值,不要仅是基于P值而做出科学结论或政策决定,而是要对具有统计显著意义的结果进行数据分析描述,还应对所有统计试验以及计算中做出的选择进行合理解释,否则结果很有可能看起来不可靠。
参考文献:
[1]: 数理统计学讲义. 陈家鼎,孙山泽,李东风,刘力平.高等教育出版社
[2]: https://www.sohu.com/a/193496957_498147(p值的现代争议)