每天高频算法题-DAY3

题目一

在一个 n * m 的二维数组中，每一行都按照从左到右 非递减 的顺序排序，每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

力扣https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/

加入目标数为25 我们从右上角开始查询  它列是有序的 也就是每行末尾的值是最大的 所以25>15

就能说明目标值肯定不在第一行里面... 一直判断到25>24 且<30 就能说明它在第五行里面

然后在这个行里面进行二分 找到值

 写完打大思路开始做题 做不出来 结论是 不要用二分 1如果用二分整体代码会十分复杂 

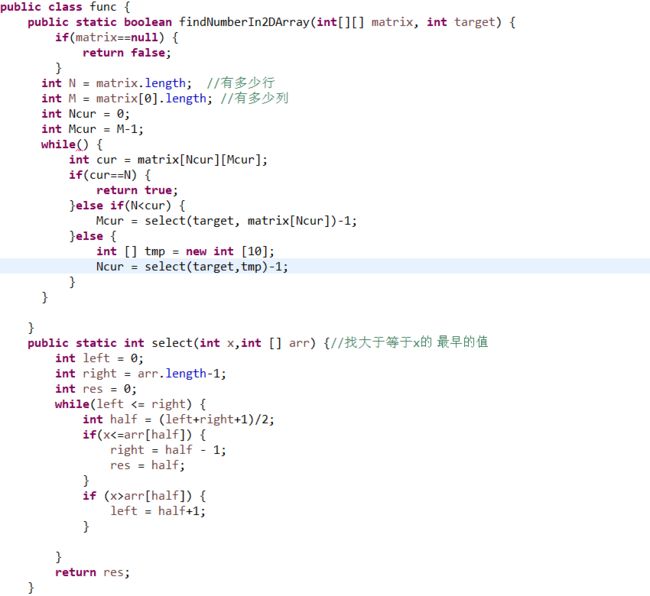
给大伙看一下我试图二分的代码(而且没写完)

 列方向上的二分还需要临时数组(贼麻烦)

然后这个是直接的遍历

class Solution {
    public static boolean findNumberIn2DArray(int[][] matrix, int target) {
			if(matrix.length == 0) {
			return false;
		}
		int row = 0;
		int col = matrix[0].length - 1;
		while (row < matrix.length && col > -1) {
			if (matrix[row][col] == target) {
				return true;
			} else if (matrix[row][col] > target) {
				col--;
			} else {
				row++;
			}
		}
		return false;
    }
}

题目二

有点飞仙题

有n个打包机器从左到右一字排开，上方有一个自动装置会抓取一批放物品到每个打包机上放到每个机器上的这些物品数量有多有少，由于物品数量不相同，需要工人将每个机器上的物品进行移动从而到达物品数量相等才能打包。每个物品重量太大、每次只能搬一个物品进行移动，为了省力，只在相邻的机器上移动。请计算在搬动最小轮数的前提下，使每个机器上的物品数量相等。如果不能使每个机器上的物品相同，返回-1。例如[1.0.5]表示有3个机器，每个机器上分别有1、0、5个物品，经过这些轮后：第一轮：1  0＜- 5=＞1 1 4第二轮：1＜-1＜-4=＞2 1 3第三轮：2 1＜-3=＞2 2 2移动了3轮，每个机器上的物品相等，所以返回3例如[2.2.3]表示有3个机器，每个机器上分别有2、2、3个物品，这些物品不管怎么移动，都不能使三个机器上物品数量相等，返回-1

 首先狗都知道的是 如果当前包裹数不能被N整除的话可以直接排除掉

说实话这题连暴力解我都不会 还是看答案的

我们假定一个i位置 以这个位置分界 左侧右侧 假如说左侧有a个 那么想要平衡 左侧应该有 总数/机器数*左侧机器数 用它和实际包裹数相比较 如果多了 就应该往外仍 如果少了就应该拿(注意这个位置上本身也有包裹 但是先不考虑) 

原理就是 既然一次传送包裹 最多也就送一个 那么当前位置的扔的包裹和当前位置收的包裹取最大值 就等于当前位置的包裹绝对流动数(因为扔一个包裹和接收一个包裹是同时进行的) 那么我们遍历所有位置 找到的最大的包裹流动数 就是答案 因为有些地方包裹传送到一定位置就停在这里了 但是其他位置的传送还没停止 所以我们选一个最大的位置 一定是经历了所有传送的地方(如果我左边 传送几轮 右侧传送几轮呢 那也不影响啊 取最大值 那我左侧传送5轮 然后 右侧再传送六轮呢 共传送十一轮 你输出的结果是6轮啊 注意提给条件最小轮数)

coding的时候想想 这个数组 怎么做呢 直接暴力求的话 也要个O(N²) 

先求个累加和数组sum吧 然后每个位置就是 左侧的包裹数sum[i-1]    右侧的包裹数sum[i+1]-sum[i] 在按照原计划和之前的和N/arr.length * (i-1+1) 以及 N/arr.length * (arr.length-i-1)

题目三

给定一个数组arr长度为N，你可以把任意长度大于0且小于N的前缀作为左部分，剩下的作为右部分。但是每种划分下都有左部分的最大值和右部分的最大值，请返回最大的，左部分最大值减去右部分最大值的绝对值。

究极飞仙题

首先这个答案肯定是 整个数组的最大值-某个值对吧 不可能说 我明明可以用最大值减 而去用更小的 那不纯浪费吗 (是不是感觉哪不对 又说不清? 那如果最小值和最大值分在一边了 那我岂不是就减不到最小值了? 事实上是不会出现这种情况的 每两个元素即使是相邻的元素 只要你想 就可以分在不同的两边) 

最大值确定一定要有了 那另一个呢?

哎 最尿性的来了啊 我们选择第一个和最后一个数组元素里面 更小的那个(对应最大值为左半部分和对应最大值为右半部分) 假如啊 我们的数组最大值 为左侧 那么右侧怎么看呢 我们肯定要找一个最小的最大值吧?如果这个N-1位置的值为右侧最大值 那么左边有比它大的不考虑 因为这不是最大值最小的情况 那如果N-1右侧有比它小的呢? 那它那他也不是最大值(不是说我可以选择两个部分啊 一半部分敲定了之后 另一半也就确定了 剩下的全是另一半)

8 9 4 3  我不可能把4留着吧? 我肯定得把4放在最大值那一边去 8 9  0 3 这咋画 也是3为右侧最大值 0划分到左侧没有最大值大 划分到右侧没有最边界的值大 

然后最大值分到右侧同理

捋一捋思路 遍历数组找一个最大值 然后最大值减去两个边界0 N-1的值中的更小值 为答案

这题还要code???