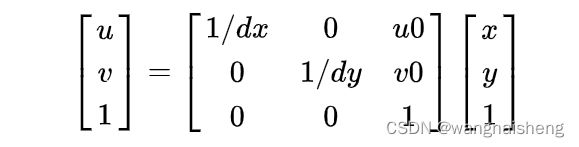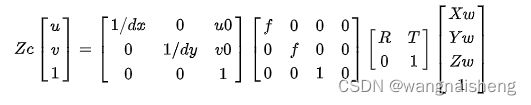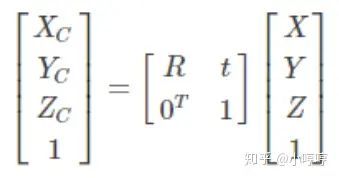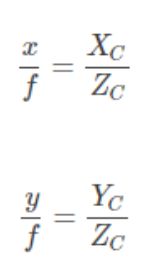机器视觉中三大坐标系及其相互关系；世界、相机、图像、像素坐标系之间的关系

一、机器视觉中三大坐标系及其相互关系

机器视觉系统有三大坐标系，分别是：1、世界坐标系，2、摄像机坐标系，3、图像（像素）坐标系。

1、世界坐标系

世界坐标系（Xw，Yw，Zw）是目标物体位置的参考系，根据运算方便自由设置圆点位置，可以位于机器手底座或者机器手前端执行器上。

其主要作用有

(1)盛放物体的三维坐标；

(2)标定的时候根据原点确定标定物的位置；

(3)给定出两个摄像机相对于世界坐标系的位置，从而求出两个或多个相机之间的坐标关系；

2、摄像机坐标系

摄像机坐标系（Xc，Yc，Zc）是摄像机在自己角度上的坐标系，原点在摄像机的光心上，Z轴与摄像机光轴平行，即摄像机的镜头拍摄方向。

3、图像（像素）坐标系

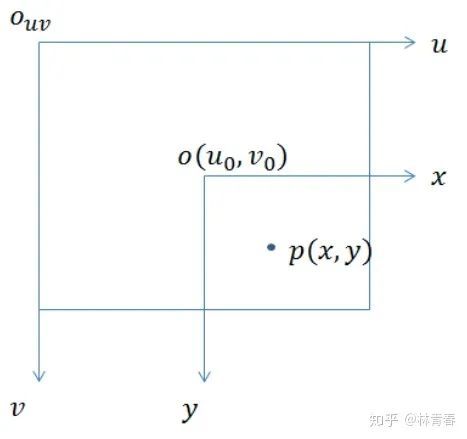
3.1、图像坐标系

图像坐标系（x，y）单位米或毫米，是连续图像坐标或者空间坐标，以图片对角线交点作为基准原点建立的坐标系。

3.2、像素坐标系

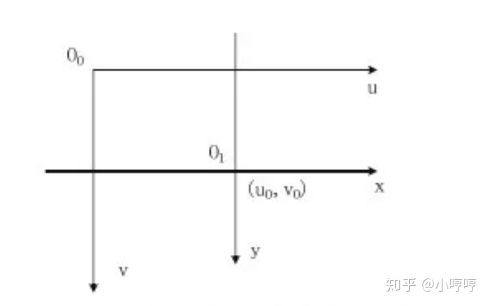
像素坐标系（u，v）单位尺度为一个pixel，是离散图像坐标或像素坐标，原点在图片的左上角。

4、坐标系之间的关系

当我们在图片中确定了某个物体的位置，如何让机器手去到空间中的实际位置进行抓取呢？这就需要对坐标进行转换。而从像素点到空间点的转换与空间点到像素点的转换是相反的，我们先将后者的推导过程。

4.1、图像坐标系与像素坐标系

图像坐标系与像素坐标系的关系为：

 

 

 

dx代表一个像素的宽度（x方向），与x同单位，x/dx表示x轴上有多少个像素，同理y/dy表示y轴上的像素个数，(u0，v0)是图像平面中心。

将上述关系转换为矩阵形式：

 

 

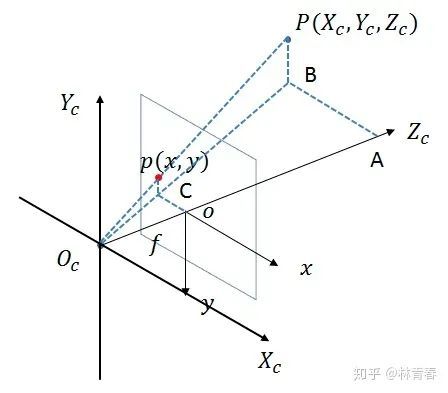
4.2、相机坐标系与图像坐标系

从相机坐标系到图像坐标系是一个三维坐标到二维坐标（3D->2D）的过程，称之为透视投影变换。为了求解它们之间的关系，将普通图像坐标（x，y）拓展为齐次坐标（x，y，1）。空间中的某点，投影到图像平面上的点与相机的光心在一条直线上。以光心为原点建立相机坐标系：

根据相似三角形关系可以得到以下：

 

4.3、世界坐标系与相机坐标系

世界坐标（Xw，Yw，Zw）与相机坐标（Xc，Yc，Zc）同为三维坐标（右手系，三轴互相垂直），两个坐标系的关系为刚体变换（刚体变换：当物体不发生形变时，对一个几何物体作旋转，平移的运动）。可以先凭空想象下，有两个坐标系A与B，如何将A坐标系下的坐标转换到B坐标系表示，首先将A坐标系以原点为基准任意旋转，使其x轴，y轴，z轴与B坐标轴平行且同方向，接着平移AB坐标系原点的直线距离，就可以将A坐标系下的坐标转换到B坐标系，这个旋转Rotation与平移Transport就是需要求得的两个三维坐标之间的关系。

用以下等式表示两个坐标系之间的关系：

4.4、从世界坐标到像素坐标

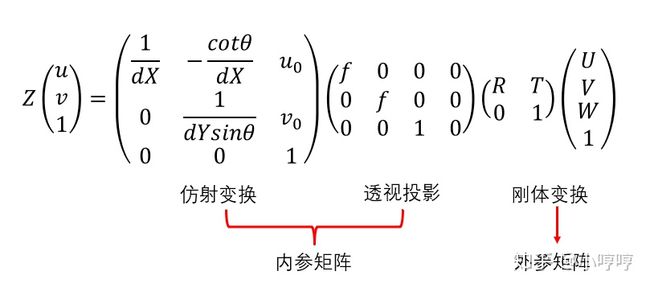
综合上面推导的过程，世界坐标（Xw，Yw，Zw）—>相机坐标（Xc，Yc，Zc）—>图像坐标（x，y）—>像素坐标（u，v），以上顺序用矩阵表示为不断左乘下一步，即：

等式右边的前两个矩阵称的乘积为相机内参，第三个矩阵称为相机外参，后面的单目相机标定，就是为了求解相机的内外参数。

 转至：总结|机器视觉中三大坐标系及其相互关系

 

二、世界、相机、图像、像素坐标系之间的关系

世界坐标系：就是客观三维世界的绝对坐标系，也成为客观坐标系。在环境中还选择一个参考坐标系来描述摄像机和物体的位置，该坐标系称为世界坐标系。设该坐标系下存在一个物体P的坐标为(X, Y, C)

相机坐标系：以相机光点为中心，X，Y轴平行于图像的两条边，光轴为Z轴所建立的坐标系。用（Xc, Yc, Zc)表示物体P在相机坐标系下的位置。

世界坐标系和相机坐标系的关系：刚体变换---世界坐标系中的某一点可以通过旋转R和平移t转换成相机坐标系中的一点。（二者都是三维的，只是坐标系不同）

R是3x3的矩阵，t是3x1的向量

图像坐标系：以图像中心为坐标原点，X，Y轴平行于图像两边，可以用（x, y）表示物体P的坐标值。（单位是mm，代表该像素在图像中的位置）

相机坐标系和图像坐标系之间的关系：透视投影---与小孔成像原理类似。

与焦距相关

转换成齐次坐标系和矩阵来表示：

像素坐标系：以图像左上角为原点，X,Y轴分别平行于图像两边的坐标系。用(u, v)表示其坐标值。

图像坐标系和像素坐标系的关系：仿射变化---图像坐标系中的（x, y）单位是mm，其中dx代表每一个像素的物理距离是多少，即单位是mm/pix。所以x*(1/dx)的单位就是像素pix。

图像坐标系和像素坐标系的关系，(u0, v0)代表该中心点在像素坐标系下的坐标。

图像坐标系上的某一点坐标为(x, y)，相对于其原点(u0, v0)的像素坐标为(x/dx, y/dy)，相对于像素坐标原点的坐标如上式子，即（u,v） = (x/dx+u0, y/dy+v0)

总结：世界坐标系中的某一点(X, Y, Z)可以通过刚体变换、透视投影、仿射变化得到它在图像中的位置。

就上面这个式子可以看出来：如果我们需要对一个成像系统建模，那就需要知道内参和外参。在实际的生活中，获取内参和外参的方法就是标定。

转至：世界、相机、图像、像素坐标系之间的关系 - 知乎