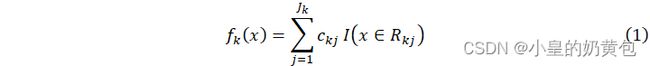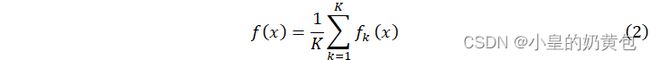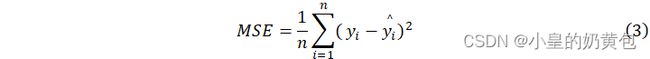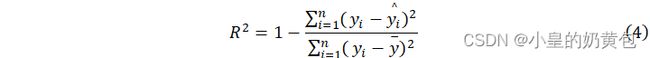随机森林回归算法的Python实现与应用

摘要

    随机森林回归是一种集成学习算法，通过组合多个决策树来实现回归任务，构建多个决策树，并将它们组合成一个强大的回归模型。本文将会从随机森林回归算法的算法原理、Python实现及实际应用进行详细说明。

1 绪论

    在现在的数据分析及数学建模等竞赛中，机器学习算法的使用是很常见的，除了算法实现还需要对赛题或自己所获得的数据集进行数据预处理工作，本文默认读者的数据均已完成数据预处理部分。

2 材料准备

    Python编译器：PyCharm社区版或个人版等

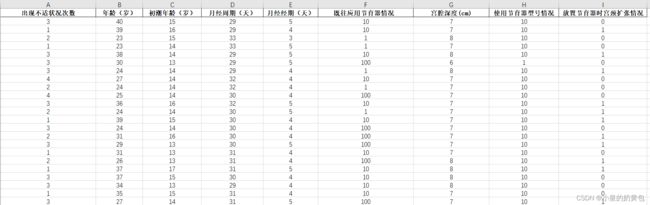
    数据集：本文所使用的数据集样例如图2.1所示，如有需要，请私发笔者电子邮箱，获取元数据。

图2.1 数据集样例  

3 算法原理

        随机森林回归是一种集成学习算法，它通过组合多个决策树来实现回归任务，通过构建多个决策树，并将它们组合成一个强大的回归模型，具体步骤如下：

        Step 1：随机选择一个样本子集作为该决策树的训练集。

        Step 2：随机选择一部分特征（总特征数的平方根）作为该决策树的特征集。

        Step 3：基于训练集和特征集构建决策树，直到达到预定的叶子节点数或无法分割为止。

        Step 4：重复以上步骤，建立多颗决策树。

        Step 5：对于一个新的样本，将它输入到每棵决策树中，得到多个预测结果。

        Step 6：对多个预测结果进行平均，得到最终的预测结果。

        其算法公式基于决策树回归模型，每个决策树的预测函数可以表示为如公式（1）所示：

        式中：k表示第k棵决策树， 表示输入样本，表示第棵决策树的叶子节点数，表示第棵决策树第个叶子节点的预测值，表示第棵决策树第叶子节点的样本集合。

        多棵决策树的预测函数可以表示为：

  

        式中：K表示决策树的数量。

         在模型评估上，随机森林回归的常用指标包括均方误差（MSE）和R-squared（R2），一般来说，MSE的值越小，说明模型对数据的拟合程度越好，R2的值越接近于1，说明模型对数据的拟合程度越好，反之亦然。其计算公式如下：

        式中，表示样本数量， 表示第 个样本的真实值， 表示第 个样本的预测值。

        式中： 表示所有样本真实值的平均值。

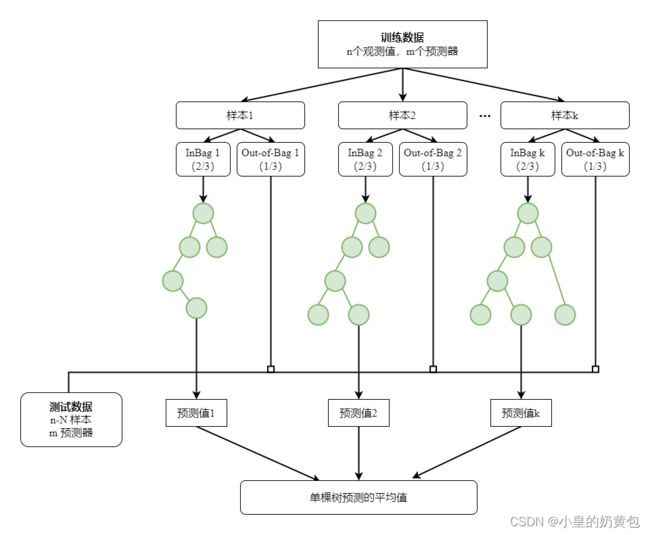
        其算法原理示意图如图3.1所示：

图3.1 随机森林回归原理示意图

 4 算法Python实现

  4.1 数据加载

        此处利用pandas库进行读取数据，第一列特征为目标变量，其余的列特征作为自变量。

import pandas as pd
# 读取数据
data = pd.read_excel('DataRFL.xlsx')
# 分割自变量和目标变量
X = data.iloc[:, 1:]
y = data.iloc[:, 0]

4.2 将数据集切分为训练集和测试集

        使用train_test_split函数对数据集进行切分，30%作为测试集，70%作为训练集。

from sklearn.model_selection import train_test_split
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

4.3 利用训练集进行模型训练

        利用70%的样本数据进行模型训练，即X_train和y_train，Python有随机森林回归的库，直接调用即可，简单实现自己的需求。

from sklearn.ensemble import RandomForestRegressor
# 训练模型
rf = RandomForestRegressor(n_estimators=100, random_state=42)
rf.fit(X_train, y_train)

4.4 结果预测

        本文使用30%测试集进行拟合，后文的拟合效果评估需要这一步，如果全部数据均是训练集，模型的拟合效果是说明不了的。

# 预测结果
y_pred = rf.predict(X_test)

4.5 模型评估

        机器学习回归不像是机器学习分类，机器学习分类算法的评估是通过准确率、精确率、召回率和F1-Score去评估，而回归算法的评估因子是通过均方差MSE和R方值进行说明的，这两者的评估原理和数值的说明如前文所述。

from sklearn.metrics import mean_squared_error, r2_score
# 计算MSE和R-squared
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 输出模型评估结果和目标方程
print('MSE:', mse)
print('R-squared:', r2)

4.6 目标方程的输出

        回归算法的模型是一条回归公式，其各特征的系数由特征重要性所决定。

# 输出目标方程
print("目标方程：")
for i, feature in enumerate(X.columns):
    print("{} * {} +".format(rf.feature_importances_[i], feature), end=' ')

4.7 绘制特征重要性条形图

        有一些题目需要确认影响该模型的关键因素或影响某物品的决定因素等，可以通过各特征在算法的重要性进行说明。

import matplotlib.pyplot as plt
# 绘制特征重要性条形图
feature_importance = rf.feature_importances_
feature_names = X.columns.tolist()
sorted_idx = feature_importance.argsort()
#避免中文乱码
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
plt.barh(range(len(feature_importance)), feature_importance[sorted_idx])
plt.yticks(range(len(feature_importance)), [feature_names[i] for i in sorted_idx],fontsize=5)
plt.xlabel('特征重要性')
plt.ylabel('特征名称')
plt.title('随机森林回归特征重要性')
plt.savefig('随机森林回归特征重要性',dpi=300)

4.8 结果输出

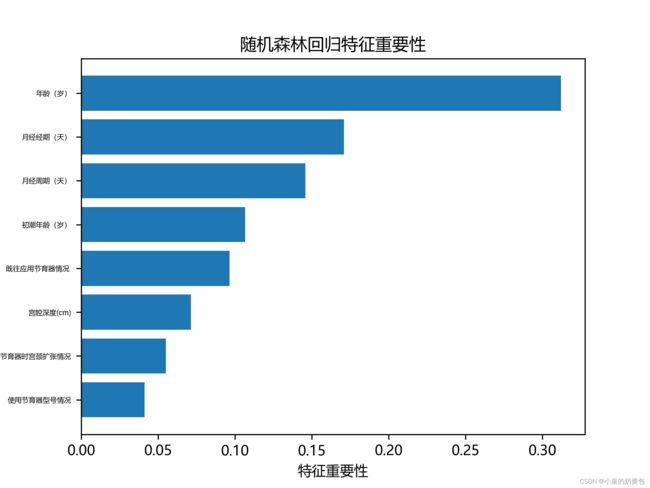
        控制台结果输出如图4.1所示，特征重要性条形图输出如图4.2所示。

 图4.1 结果输出

图4.3 特征重要性条形图

 4.9 结果说明

        在本文的拟合中，MSE为0.87，确实很小，说明模型对训练集数据的拟合效果非常好，但并不一定代表模型的泛化能力强，即能够对新的未见过的数据进行准确预测。

        R2的值是负值，说明模型对目标变量的解释能力比随机猜测还要差。R-squared的取值范围是0到1之间，越接近1表示模型对目标变量的解释能力越强，越接近0表示模型对目标变量的解释能力越弱，而如果是负数，则说明模型的表现不如随机猜测。

        所以本文所建立的模型是不适用的，应该考虑别的算法，或者思考自己的数据预处理是否有问题。

4.10 完整代码实现

import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

# 读取数据
data = pd.read_excel('附件0.2.xlsx')

# 分割自变量和目标变量
X = data.iloc[:, 1:]
y = data.iloc[:, 0]
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 训练模型
rf = RandomForestRegressor(n_estimators=100, random_state=42)
rf.fit(X_train, y_train)

# 预测结果
y_pred = rf.predict(X_test)

# 计算MSE和R-squared
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 输出模型评估结果和目标方程
print('MSE:', mse)
print('R-squared:', r2)
# 输出目标方程
print("目标方程：")
for i, feature in enumerate(X.columns):
    print("{} * {} +".format(rf.feature_importances_[i], feature), end=' ')

# 绘制特征重要性条形图
feature_importance = rf.feature_importances_
feature_names = X.columns.tolist()
sorted_idx = feature_importance.argsort()

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
plt.barh(range(len(feature_importance)), feature_importance[sorted_idx])
plt.yticks(range(len(feature_importance)), [feature_names[i] for i in sorted_idx],fontsize=5)
plt.xlabel('特征重要性')
plt.ylabel('特征名称')
plt.title('随机森林回归特征重要性')
plt.savefig('随机森林回归特征重要性',dpi=300)

5 算法应用

        随机森林回归算法可以应用于销售量的预测、房价的预测和股票价格的预测（股市有风险，入行需谨慎）等领域，具体可以阅读相关领域的文献。

6 结论

        本文对随机森林回归算法对原理说明、算法的Python实现及算法应用进行了简要的说明，文中给出了一个拟合效果不佳的模型进行示例，待日后有合适的训练数据再补充说明。

7 备注

        本文为原创文章，禁止转载，违者必究。如需原始数据，请点赞+收藏，然后私聊笔者或在评论区留下你的邮箱，即可获取原始数据一份。