【C语言初阶(16)】操作符2
文章目录
- Ⅰ关系操作符
- Ⅱ 逻辑操作符
-
- ⒈操作符介绍
- ⒉短路求值
- Ⅲ 条件操作符
- Ⅳ 逗号表达式
- Ⅴ 下标引用、函数调用和结构成员
-
- ⒈[ ] 下标引用操作符
- ⒉( ) 函数调用操作符
- ⒊结构体成员访问操作符
- Ⅵ 表达式求值
-
- ⒈隐式类型转换(整型提升)
- ⒉算术转换
- ⒊操作符的属性
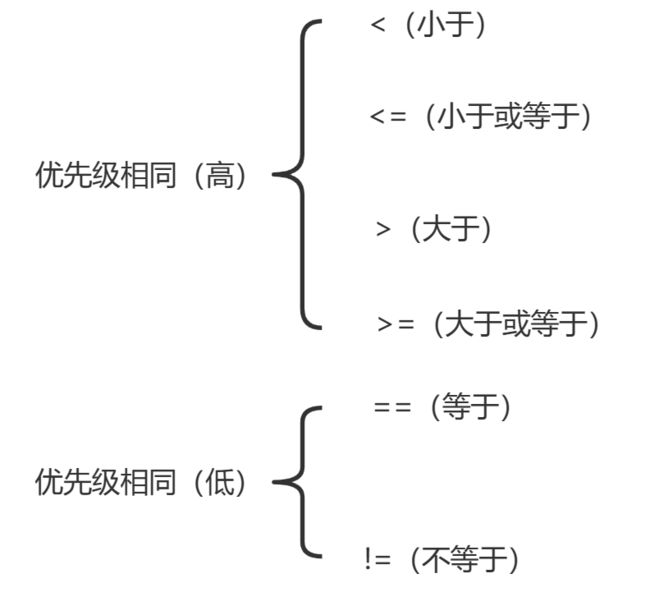
Ⅰ关系操作符
- 在 C 语言中,使用关系操作符来判断两个数之间的大小关系。
- 关系运算符都是双目运算符,其结合性均为从左到右。
- 关系运算符的优先级低于算术运算符,高于赋值运算符。
Ⅱ 逻辑操作符
- 逻辑运算符获得的是一个逻辑值,逻辑值只有 “ 真 ” 或 “ 假 ”两种状态。
| 运算符 | 含义 | 优先级 | 举例 | 说明 |
|---|---|---|---|---|
| ! | 逻辑反 | 高 | !a | 如果 a 为真,则 !a 为假;如果 a 为假,则 !a 为真。 |
| && | 逻辑与 | 中 | a && b | 只有 a 和 b 同时为真,结果才为真;a 和 b 只要有一个是假的,则结果为假。 |
| || | 逻辑或 | 低 | a || b | 只要 a 或 b 中有一个为真,则结果为真;a 和 b 同时为假,结果采薇假。 |
⒈操作符介绍
1. “ ! ” 逻辑反
- 逻辑反操作符在单目操作符那块讲过了,这里就不过多赘述。
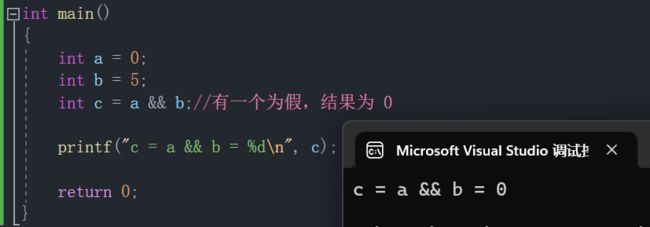
2. “ && ” 逻辑与
- 全真则真。
- 只有 a 和 b 同时为真,整个表达式的结果才为真。
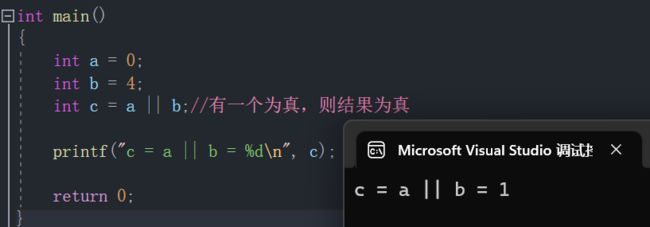
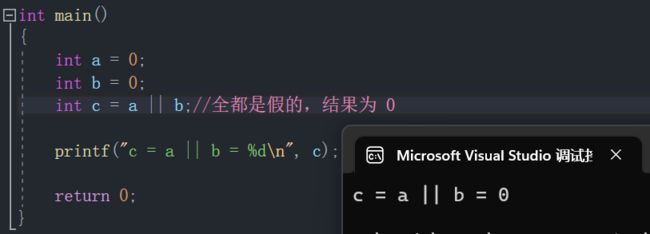
3. “ || ” 逻辑或
- 全假则假。
- a “ 或 ” b ,两个只要有一个是真的,表达式结果则为真,a 和 b 全是假的表达式结果才是假的。
⒉短路求值
- 短路求职又称最小化求值,是一种逻辑运算符的求值策略。
- 只有当第一个运算数的值无法确定逻辑运算的结果时,才对第二个运算数进行求值。
先说结论
- &&:左边为假,右边就不计算了。
- | | :左边为真,右边就不计算了。
举个栗子
- 下面代码 a b c d 的结果分别是多少?
#include - 对 a 采用的是后置++,所以是先拿 a = 0 的值进行逻辑运算,而逻辑与一旦看到这个 0 后面不管有再多的表达式都不会去运算了,因为第一个都是 0 了,整个表达式的结果肯定是 0。
- 然后再对 a 进行 +1。
再看个栗子
- 下面代码的 a b c d 的结果分别是多少?
#include - 第一个运算数是 a++,先拿 a = 0 去进行逻辑或判断,无法确定逻辑运算的结果,对第二个运算数 ++b 进行值。
- ++b 是前置 ++,b 的值变为 3 ,则第二个逻辑或的左边为真,根据短路求值的原则,右边的 d++ 无须再进行计算。
Ⅲ 条件操作符
- 有一个操作数的操作符称为单目操作符,有两个操作数的操作符称为双目操作符,C 语言中还有唯一的一个有三个操作数的三目操作符,它的作用是提供一种简写的方式来表示 if-else 语句。
- 这个三目操作符的语法格式为:
表达式1 ? 表达式2 : 表达式3;
-
表达式 1 是条件表达式,如果结果为真,则返回表达式 2;如果为假,则返回表达式 3。
-
例如:求两个数中得较大值。
if(a > b)
{
max = a;
}
else
{
max = b;
}
- 可以简写成:
max = a > b ? a : b;
//a > b 吗?,大于则返回 a,否则返回 b
Ⅳ 逗号表达式
语法格式
表达式1, 表达式2, 表达式3, …,表达式N
逗号表达式的运算过程
- 从左往右逐个计算表达式。逗号表达式作为一个整体,它的值为最后一个表达式(即表达式n)的值。
举个栗子
再举个栗子
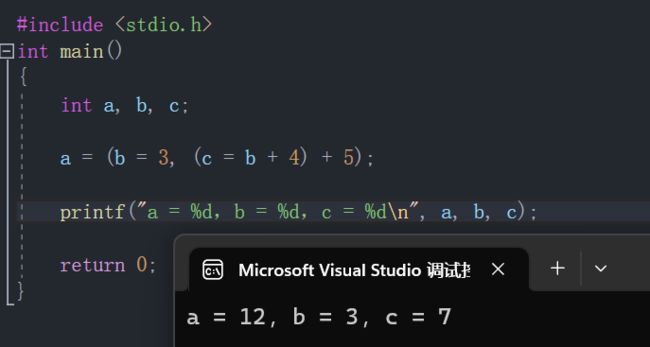
a = (b = 3, (c = b + 4) + 5)
- 先将变量 b 赋值为 3,然后变量 c 赋值为 b + 4 的和,也就是 7,接下来把 c 的值加上 5,赋值给变量 a,得到变量 a 的值就是 12。
- 逗号运算符的优先级是最低的,虽然 c = b + 4 用优先级最高的小括号运算符括起来,但只要在逗号表达式内,都应该从左到右依次执行每个表达式。
逗号表达式注意事项
- 在 C 语言中看到逗号,不一定就是逗号表达式,因为在有些时候,逗号仅仅是被用作分隔符而已。
- int a, b, c;
- scanf(“%d %d %d”,&a, &b, &c);
- 这里的逗号都是作为分隔符使用,而不是运算符。
Ⅴ 下标引用、函数调用和结构成员
⒈[ ] 下标引用操作符
- 操作数:一个数组名 + 一个索引值。
int arr[10];//创建数组
arr[9] = 10;//实用下标引用操作符。
- 的两个操作数是arr和9。
⒉( ) 函数调用操作符
接收一个或者多个操作数
- 第一个操作数是函数名;
- 剩余的操作数就是传递给函数的参数。
//函数定义
int Add(int x, int y)
{
return x + y;
}
int main()
{
int a = 10;
int b = 20;
//函数调用
int c = Add(a, b);//这里的小括号 () 就是函数调用操作符
// () 的操作数为:Add,a,b
return 0;
}
- 函数调用的操作数至少有一个(函数名),可以没有参数。
⒊结构体成员访问操作符
| 操作符 | 语法格式 |
|---|---|
| . | 结构体 . 成员名 |
| -> | 结构体指针 -> 成员名 |
** 1. “ . ” 操作符**
#include 2. “ -> ” 操作符
#include Ⅵ 表达式求值
表达式的定义
- 用操作符和括号将操作数连接起来的式子,称为表达式。
- 下面是几个表达式的例子:
- 1 + 1
- 'a' + 'b'
- a + b
- a + 'b' + pow(a,b) * 3 / 4 + 5
- 表达式可以很简单(像1+1),也可以很复杂(像a + ‘b’ + pow(a,b) * 3 / 4 + 5)。那么涉及复杂的表达式,就需要讨论计算的夏侯顺序问题了。
表达式的求值顺序
- 表达式求值的顺序一部分是由操作符的优先级和结合性决定。
- 优先级:2 + 6 / 3,这里的优先级就是先算除法再算加法。
- 结合性:b = 2 + 3 + 4,优先级相同时,一个表达式中该先算谁就看结合性了,+ 号的结合性是从左到右,也就是说先算 2 + 3 再算 5 + 4。
- 有了优先级和结合性之后就能大概确定表达式的计算路径。
- 同样 ,有些表达式的操作数在求值的过程中可能需要转换为其他类型。
⒈隐式类型转换(整型提升)
- C 的整型算术运算总是至少以默认整型类型的精度来进行的。
- 为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型,这种转换称为整型提升。
- 只要是放在表达式中的字符和短整型,在使用时就会进行整型提升。
整型提升的意义
- 表达式的整型运算要在 CPU 的相应运算器件内执行,CPU 内整型运算器(ALU)的操作数的字节长度一般就是 int 的字节长度,同时也是 CPU 的通用寄存器的长度。
- 因此,即使两个 char 类型的相加,在 CPU 执行时实际上也要先转换为 CPU 内整型操作数的标准长度。
- 通用 CPU 是难以直接实现两个 8 比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。
- 所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为 int 或 unsigned int,然后才能送入 CPU 去执行运算。
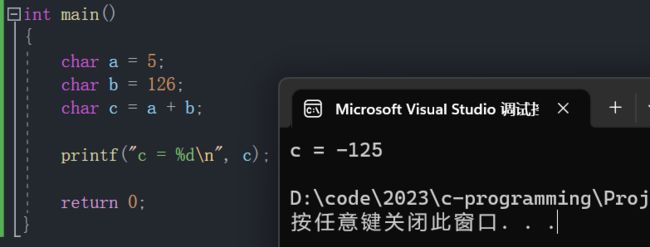
为啥下面代码的结果会是 -125?
- a 和 b 是 char 类型的数据,在运算之前默认将它们转换成整型然后再参与运算。
- 又因为 a 和 b 是 char 达不到整型的大小(4字节),所以会将 a 和 b 进行整型提升。
- 加法运算完成之后,结果将被截断,然后再存储于 a 中。
如何进行整型提升?
整形提升是按照变量的数据类型的符号位来提升的
- 负数的整型提升,字有点多,讲解放到代码框里。
char c1 = -1;//-1 是整数,32 个比特位
- -1 的补码是 1111 1111 1111 1111 1111 1111 1111 1111
- 将结果往 c1 存的时候因为 c1 是 char 放不下这么多比特位,于是就发生了截断
- 将最后 8 个比特位截了下来放到变量 c1 里面去,c1 里存的是 1111 1111
- 现在要对 c1 进行整型提升,c1 的类型是 char ,意味着 c1 是个有符号 char,
- 所以会将在 c1 中存储的二进制序列 1111 1111 里最高位的那个 1 解读为符号位
- 符号位是 1 表示它是负数,对 c1 进行整型提升就会在高位补原符号位的 1
- 提升之后的结果为 1111 1111 1111 1111 1111 1111 1111 1111 1111
- 正数的整型提升
char c2 = 1;
- 变量c2的二进制位(补码)中只有8个比特位:0000 0001
- 因为 char 为有符号的 char,最高位又是个 0
- 所以整形提升的时候,高位补充符号位,即为 0
- 提升之后的结果是:0000 0000 0000 0000 0000 0000 0000 0001
解析之前的代码
- 将 5 的二进制补码最后 8 位截断,然后赋给 a;
- a 里存放的补码为 0000 0101
- 将 126 的二进制补码最后 8 截断,然后赋给 b;
- b 里存放的补码为 0111 1110
- 现在要将 a 和 b 里存的补码进行相加,但是 a 和 b 达不到整型,所以进行整型提升
- a 符号位为 0,整型提升高位补 0,结果为 0000 0000 0000 0000 0000 0000 0000 0101
- b 符号为为 0,整型提升高位补 0,结果为 0000 0000 0000 0000 0000 0000 0111 1110
- 现再将 a 和 b 提升后的结果相加,结果为 0000 0000 0000 0000 0000 0000 1000 0011
- 将结果赋给 c,c 是 char 存不下这么多比特位,进行截断,将 1000 0011 赋给 c
- 因为要打印 c,所以对 c 进行整型提升,符号位为 1,高位补 1
- c 的补码为 1111 1111 1111 1111 1111 1111 1000 0011
- 将结果转成原码然后进行打印;
- c 的原码为 1000 0000 0000 0000 0000 0000 0111 1101
- 所以 -125 就是这么来的
整型提升的例子
//实例1
int main()
{
char a = 0xb6;
short b = 0xb600;
int c = 0xb6000000;
if (0xb6 == a)
{
printf("a");
}
if (0xb600 == b)
{
printf("b");
}
if (0xb6000000 == c)
{
printf("c");
}
return 0;
}
c
- 实例 1 中的 a,b 都要进行整形提升,但是 c 不需要整形提升;
- a,b 整形提升之后变成了负数,所以表达式 a == 0xb6 , b == 0xb600 的结果是假;
- 但是 c 不发生整形提升,则表达式 c == 0xb6000000 的结果是真。
//实例2
int main()
{
char c = 1;
printf("%u\n", sizeof(c));
printf("%u\n", sizeof(+c));
printf("%u\n", sizeof(-c));
return 0;
}
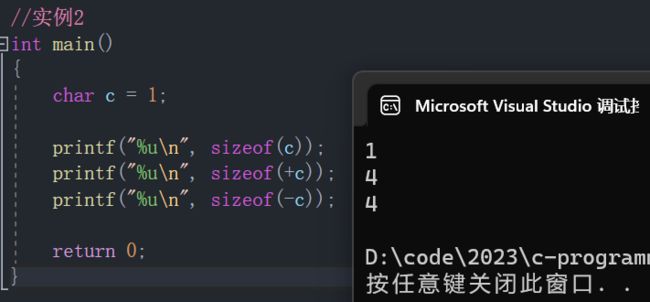
- 实例2中的 c 只要参与表达式运算,就会发生整形提升,表达式 +c 就会发生提升,所以 sizeof(+c) 是 4 个字
节; - 表达式 -c 也会发生整形提升,所以 sizeof(-c) 是 4 个字节;
- 但是 sizeof© 中的 c 并没有参与计算,无法整型提升,所以就是 1 个字节。
⒉算术转换
算术转换定义
- 大小小于整型的类型在计算的时候要进行整型提升,而大于整型的类型在计算时也会进行转换,这种转换称之为算术转换。
- 如果某个操作符的各个操作数属于不同的类型,那么除非其中一个操作数转换为另一个操作数的类型,否则操作就无法进行,下面的层次体系称为寻常算术转换。
- long double
- double
- float
- unsigned long int
- long int
- unsigned int
- int
- 如果某个操作数的类型在上面这个列表中排名较低,那么首先要转换成另外一个操作数的类型后执行运算。
- 例如:一个 float 类型的数据和一个 int 类型的数据遇到的时候,会将 int 类型的数据转换为 float 类型。
合理进行算术转换
- 算术转换需要合理进行,不然就会有一些潜在的问题。
float f = 3.14;
int num = f;//隐式转换,会有精度丢失
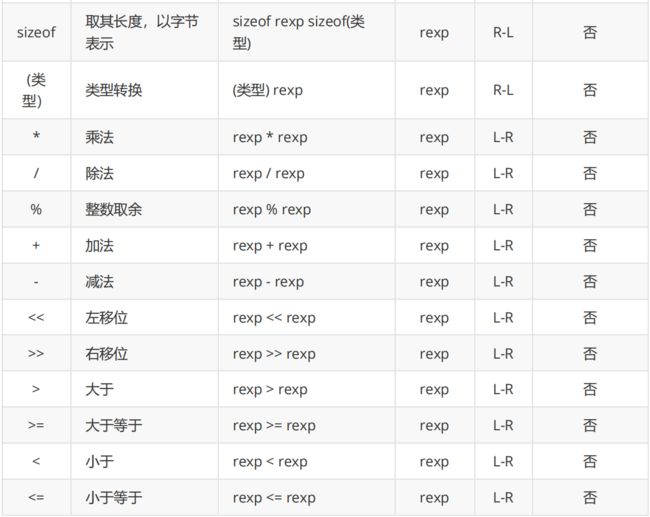
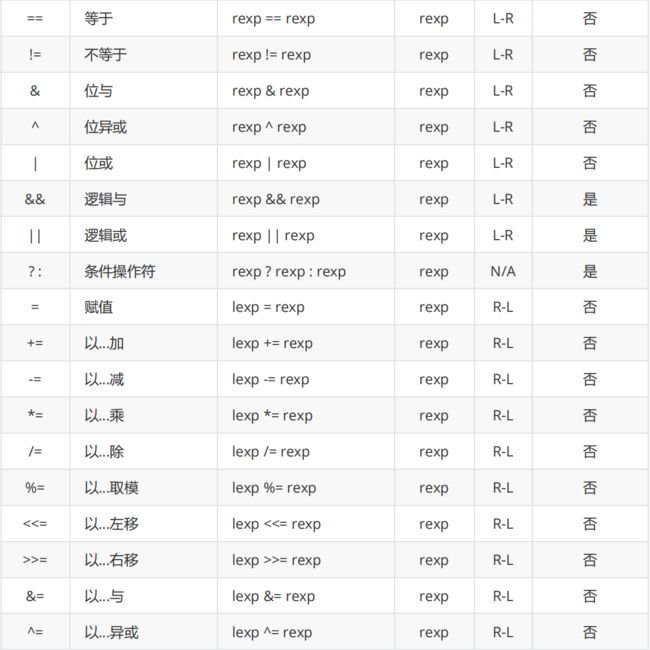
⒊操作符的属性
复杂表达式的求值有三个影响的因素
- 操作符的优先级。
- 操作符的结合性。
- 是否控制求值顺序。
- 两个相邻的操作符先执行哪个,取决于他们的优先级。如果两者的优先级相同,取决于他们的结合性。
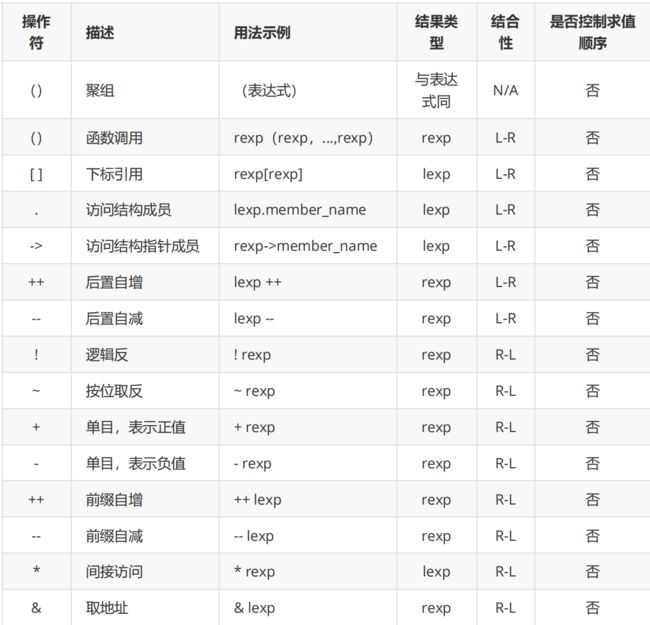
运算符的优先级和结合性表
- 操作符的优先级自上而下,从高到低。