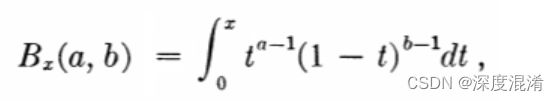C#,数值计算——不完全 Beta 函数(incomplete beta function)的源代码
Incomplete Beta Function
The incomplete beta function (also called the Euler Integral) is a generalized β-function; An independent integral (with integral bounds from 0 to x) replaces the definite integral. The formula is:
Where:
0 ≤ x ≤ 1,
a, b > 0. Note: The definition is sometimes written to include negative integers (e.g. Özçag et al., 2008) but this isn’t commonplace.
B1(p, q) is the (complete) beta function; in other words, the function becomes complete as x = 1. The incomplete beta function can also be expressed in terms of the beta function or three complete gamma functions (DiDonato & Jarnagin, 1972).
Incomplete Beta-Function Ratio
The ratio of
to
is called the incomplete beta function ratio. Represented by the symbol Ix, it is written as:
Ix (a, b) ≡ Bx(a, b) / B1(a, b).
Where a > 0, b > 0 (DiDonato & Jarnagin, n.d.).
Incomplete Beta Function Uses
The incomplete beta function and Ix crop up in various scientific applications, including atomic physics, fluid dynamics, lattice theory (the study of lattices) and transmission theory (DiDonato & Morris, 1988):
- Calculating confidence intervals for t-tests, F-tests (Besset, 2001) and those based on the binomial distribution, where the incomplete beta function is used to calculate the limits (Young et al., 1998),
- Computing the probability in a binomial distribution tail (DTIC, 1979),
- Creating cumulative probabilities for the standard normal distribution (Klugman, 2013).
- Finding a measurement larger than a certain value, for data following a beta distribution.
C# SourceCodes 源代码
using System;
namespace Legalsoft.Truffer
{
///
/// Object for incomplete beta function.
/// Gauleg18 provides coefficients for Gauss-Legendre quadrature.
///
public class Beta : Gauleg18
{
private const int SWITCH = 3000;
private const double EPS = float.Epsilon;
private const double FPMIN = float.MinValue;// / float.Epsilon;
public double betai(double a, double b, double x)
{
if (a <= 0.0 || b <= 0.0)
{
throw new Exception("Bad a or b in routine betai");
}
if (x < 0.0 || x > 1.0)
{
throw new Exception("Bad x in routine betai");
}
//if (x == 0.0 || x == 1.0)
if (Math.Abs(x) <= float.Epsilon || Math.Abs(x-1.0) <= float.Epsilon)
{
return x;
}
if (a > SWITCH && b > SWITCH)
{
return betaiapprox(a, b, x);
}
double bt = Math.Exp(Globals.gammln(a + b) - Globals.gammln(a) - Globals.gammln(b) + a * Math.Log(x) + b * Math.Log(1.0 - x));
if (x < (a + 1.0) / (a + b + 2.0))
{
return bt * betacf(a, b, x) / a;
}
else
{
return 1.0 - bt * betacf(b, a, 1.0 - x) / b;
}
}
public double betacf(double a, double b, double x)
{
double qab = a + b;
double qap = a + 1.0;
double qam = a - 1.0;
double c = 1.0;
double d = 1.0 - qab * x / qap;
if (Math.Abs(d) < FPMIN)
{
d = FPMIN;
}
d = 1.0 / d;
double h = d;
for (int m = 1; m < 10000; m++)
{
int m2 = 2 * m;
double aa = m * (b - m) * x / ((qam + m2) * (a + m2));
d = 1.0 + aa * d;
if (Math.Abs(d) < FPMIN)
{
d = FPMIN;
}
c = 1.0 + aa / c;
if (Math.Abs(c) < FPMIN)
{
c = FPMIN;
}
d = 1.0 / d;
h *= d * c;
aa = -(a + m) * (qab + m) * x / ((a + m2) * (qap + m2));
d = 1.0 + aa * d;
if (Math.Abs(d) < FPMIN)
{
d = FPMIN;
}
c = 1.0 + aa / c;
if (Math.Abs(c) < FPMIN)
{
c = FPMIN;
}
d = 1.0 / d;
double del = d * c;
h *= del;
if (Math.Abs(del - 1.0) <= EPS)
{
break;
}
}
return h;
}
public double betaiapprox(double a, double b, double x)
{
double a1 = a - 1.0;
double b1 = b - 1.0;
double mu = a / (a + b);
double lnmu = Math.Log(mu);
double lnmuc = Math.Log(1.0 - mu);
double t = Math.Sqrt(a * b / (Globals.SQR(a + b) * (a + b + 1.0)));
double xu;
if (x > a / (a + b))
{
if (x >= 1.0)
{
return 1.0;
}
xu = Math.Min(1.0, Math.Max(mu + 10.0 * t, x + 5.0 * t));
}
else
{
if (x <= 0.0)
{
return 0.0;
}
xu = Math.Max(0.0, Math.Min(mu - 10.0 * t, x - 5.0 * t));
}
double sum = 0;
for (int j = 0; j < 18; j++)
{
t = x + (xu - x) * y[j];
sum += w[j] * Math.Exp(a1 * (Math.Log(t) - lnmu) + b1 * (Math.Log(1 - t) - lnmuc));
}
double ans = sum * (xu - x) * Math.Exp(a1 * lnmu - Globals.gammln(a) + b1 * lnmuc - Globals.gammln(b) + Globals.gammln(a + b));
return ans > 0.0 ? 1.0 - ans : -ans;
}
public double invbetai(double p, double a, double b)
{
const double EPS = 1.0e-8;
double t;
double u;
double x;
double a1 = a - 1.0;
double b1 = b - 1.0;
if (p <= 0.0)
{
return 0.0;
}
else if (p >= 1.0)
{
return 1.0;
}
else if (a >= 1.0 && b >= 1.0)
{
double pp = (p < 0.5) ? p : 1.0 - p;
t = Math.Sqrt(-2.0 * Math.Log(pp));
x = (2.30753 + t * 0.27061) / (1.0 + t * (0.99229 + t * 0.04481)) - t;
if (p < 0.5)
{
x = -x;
}
double al = (Globals.SQR(x) - 3.0) / 6.0;
double h = 2.0 / (1.0 / (2.0 * a - 1.0) + 1.0 / (2.0 * b - 1.0));
double w = (x * Math.Sqrt(al + h) / h) - (1.0 / (2.0 * b - 1) - 1.0 / (2.0 * a - 1.0)) * (al + 5.0 / 6.0 - 2.0 / (3.0 * h));
x = a / (a + b * Math.Exp(2.0 * w));
}
else
{
double lna = Math.Log(a / (a + b));
double lnb = Math.Log(b / (a + b));
t = Math.Exp(a * lna) / a;
u = Math.Exp(b * lnb) / b;
double w = t + u;
if (p < t / w)
{
x = Math.Pow(a * w * p, 1.0 / a);
}
else
{
x = 1.0 - Math.Pow(b * w * (1.0 - p), 1.0 / b);
}
}
double afac = -Globals.gammln(a) - Globals.gammln(b) + Globals.gammln(a + b);
for (int j = 0; j < 10; j++)
{
//if (x == 0.0 || x == 1.0)
if (Math.Abs(x) <= float.Epsilon || Math.Abs(x=1.0) <= float.Epsilon)
{
return x;
}
double err = betai(a, b, x) - p;
t = Math.Exp(a1 * Math.Log(x) + b1 * Math.Log(1.0 - x) + afac);
u = err / t;
x -= (t = u / (1.0 - 0.5 * Math.Min(1.0, u * (a1 / x - b1 / (1.0 - x)))));
if (x <= 0.0)
{
x = 0.5 * (x + t);
}
if (x >= 1.0)
{
x = 0.5 * (x + t + 1.0);
}
if (Math.Abs(t) < EPS * x && j > 0)
{
break;
}
}
return x;
}
///
/// Returns the value of the beta function B(z,w).
///
///
///
///
public static double beta(double z, double w)
{
return Math.Exp(Globals.gammln(z) + Globals.gammln(w) - Globals.gammln(z + w));
}
}
}