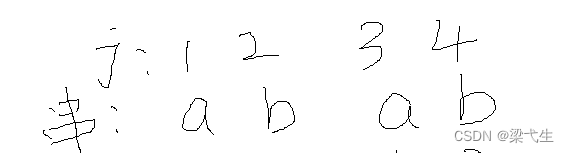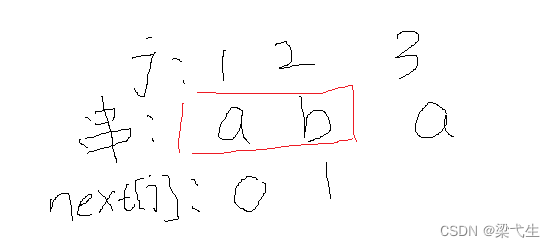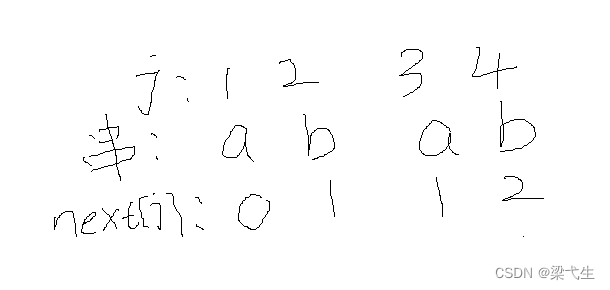数据结构之KMP算法:彻底搞懂kmp算法
数据结构的学习,kmp匹配算法困扰我许久,此处来一个总结(仅供自己复习了解参考使用),如果有不对的地方请多多指点。好了废话不多说我们直接开始好吧。
目录
关于暴力匹配原理的讲解:
kmp算法:
数据前缀表next[j]和nextval[j]怎么写出来
接下来我们来拿出来两个代码,第一个是暴力匹配代码,第二个是kmp匹配算法
暴力匹配的算法代码如下:
蛮力算法的时间复杂度
KMP算法代码示例
kmp算法的时间复杂度
首先我想再次之前先讲述一下暴力匹配解法去匹配。
关于暴力匹配原理的讲解:
现在我们主串:“abcabaababab”
模式串为:“abab”
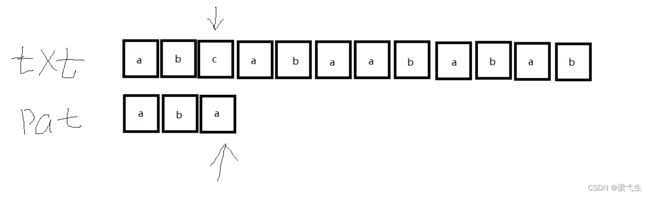
我们现在来进行暴力匹配,开始匹配。
当匹配到第三个的时候,发现不对,就将“pat”中的第一位a与“txt”中第二位进行匹配,
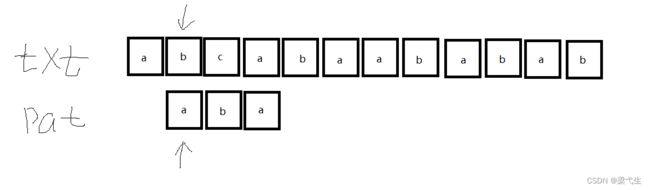
发现第一个就不匹配,那么我们继续进行匹配
还是第一个就没匹配成功,那么我们继续进行匹配
我们发现第四位还是不匹配,那么我们继续一个一个的向下匹配,这里不多赘述,直到最后匹配成功 ,如果最后也没有匹配成功,那个则返回-1,没有得到匹配的结果。
kmp算法:
单匹配查找模式,一种字符串匹配的算法,它的效率是很高的,同时比较复杂,但是要是弄清楚它的原理后,其实它是挺简单的。接下来我们先从next数组入手。
关于kmp一定要知道前缀匹配表,这样才能了解清楚什么才是kmp匹配算法。kmp中的next数组就是一个前缀表。
那么我们提到的前缀表到底有什么用呢?
其实它可以帮助我们知道怎么匹配,前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
还是以上面的例子
主串:“abcabaababab”
模式串为:“abab”
我们来写模式串的next[j]和nextval[j],如下图
那么我们先来说一下他是如何进行匹配的(然后我们再说说这个表是怎么写出来的)
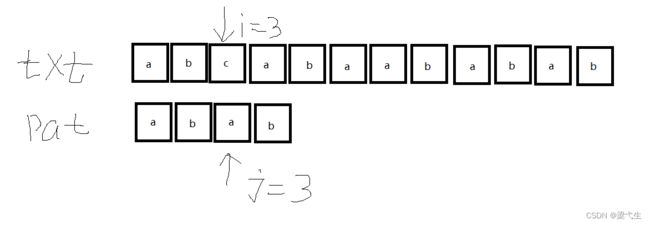
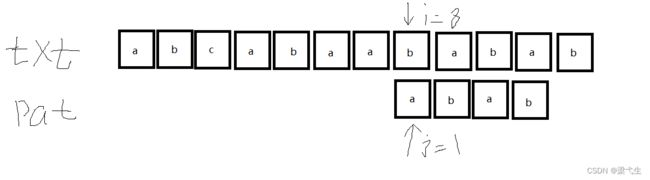
第一次匹配:在第三个位置出现了问题,那么我们进行第二次匹配
第二次匹配,我们进行查表,j=3的时候nextval是0,那么即0对应得是空,那么我们向前移一个
第三次匹配,j=1的时候还是没有匹配成功,那么我们还是向前移动一个位置
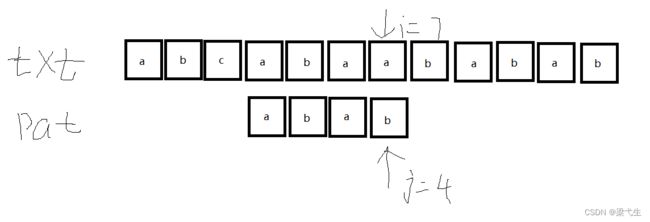
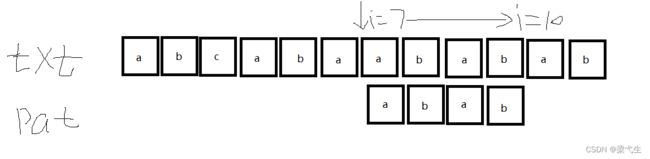
第四次匹配:这次是j=4的时候不匹配,我们看表,j=4的时候nextval[4]=1,我们看那么我们将第一位也就是a移到i=7的位置。
第五次匹配:
我们可以看到匹配成功,输出
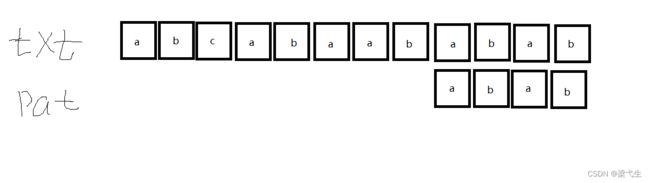
匹配成功后继续向下匹配
第七次匹配:
查表后还是向下移动一位,匹配成功
上述的过程就是进行匹配的过程,(这是本人的理解和学习,如有不同请多多指教)
数据前缀表next[j]和nextval[j]怎么写出来
我们先来讲解next[j]因为nextval[j]是按照next[j]来的。next的表格我们来写一下
我们先对串“abab”进行编号1-4。然后一般(我们是学习的严蔚敏的数据结构)我们将前两个标记为0和1,如下图所示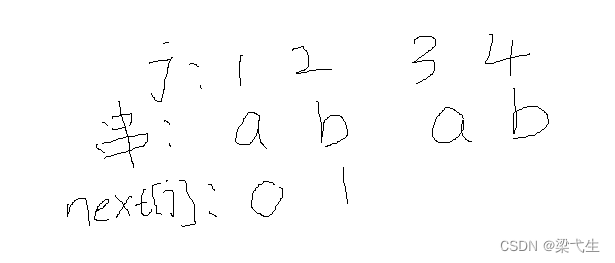
然后这里我们看第3位a,本身要不看要看它前两位的前缀和后缀
前缀:a
后缀:b
找前缀和后缀的最大匹配项,在这里没有,所以为0,那么j=3的a的next为0+1 = 1。
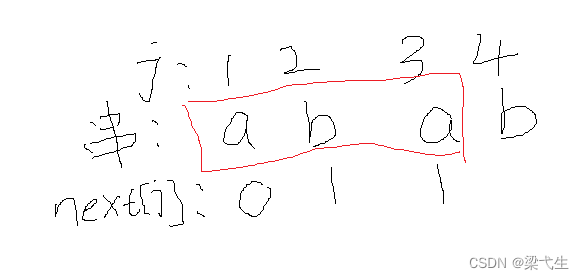
我们写出来它的网络前缀和后缀
前缀:a,ab
后缀:a,ba
这里我们看到有a与a这个最大匹配项,所以b的next值为 1 + 1=2
我们接下来写nextval的表格(要根据next表来写)
前两个数据还是0和1,如下图所示。
我们来看第三个,第三a下面是1,我们去j=1对应的元素,如果是a,那么我们将a下面的nextval的值移到j=3的a下面,如果不是a,那么我们就将a下面next的值,移到nextval。
我们来看第四个,同理,如果一致把2下面的nextval移过来,如果不一致,之间将b下面的2移到nextval那
接下来我们来拿出来两个代码,第一个是暴力匹配代码,第二个是kmp匹配算法
暴力匹配的算法代码如下:
# Brute Force Algorithm
def brute_force_algorithm(string, pattern):
n = len(string)
m = len(pattern)
for i in range(n-m+1):
j = 0
while j < m:
if string[i+j] != pattern[j]:
break
j += 1
if j == m:
print("Pattern found at index " + str(i))
# Driver code to test above
string = "abcabaababab"
pattern = "abab"
brute_force_algorithm(string, pattern)结果是两个值
蛮力算法的时间复杂度
我们来说一下它的时间复杂性
最糟糕的时间复杂性为,每一个都匹配一遍,即为每一个都匹配一遍
那么不难看出它的时间复杂性是O(n x n)。
KMP算法代码示例
下面我们来看一下kmp算法,代码如下:
# KMP Algorithm
def kmp_algorithm(string, pattern):
n = len(string)
m = len(pattern)
lps = [0] * m
j = 0
compute_lps_array(pattern, m, lps)
i = 0
while i < n:
if pattern[j] == string[i]:
i += 1
j += 1
if j == m:
print("Found pattern at index " + str(i-j))
j = lps[j-1]
elif i < n and pattern[j] != string[i]:
if j != 0:
j = lps[j-1]
else:
i += 1
def compute_lps_array(pattern, m, lps):
len = 0
lps[0] = 0
i = 1
while i < m:
if pattern[i] == pattern[len]:
len += 1
lps[i] = len
i += 1
else:
if len != 0:
len = lps[len-1]
else:
lps[i] = 0
i += 1
# Driver code to test above
string = "abcabaababab"
pattern = "abab"
kmp_algorithm(string, pattern)运行结果
kmp算法的时间复杂度
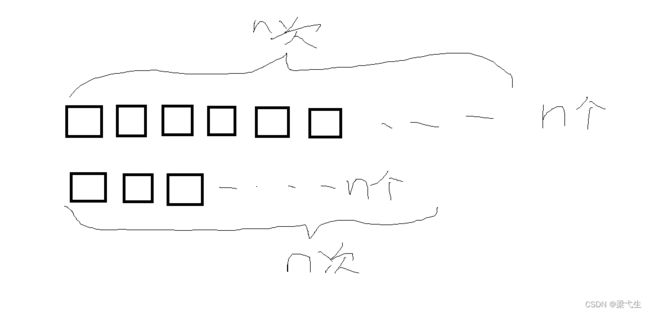
时间复杂度:假设M字符串中找N字符串的起始位置,长度分别是m和n,计算最长公共前缀后缀表长度的时候,比较的次数介于[m,2m]之间,比较模式串和子串时比较次数介于[n,2n]之间。所以时间复杂度为O(m+n)。