数学建模【嫦娥三号软着陆轨道设计与控制策略】

2014年国赛A题
pdf下载地址
https://download.csdn.net/download/yaoning6768/10641219

• 摘要

  嫦娥三号在高速飞行的情况下，要保证准确地在月球预定区域内实现软着陆，关键 问题是着陆轨道与控制策略的设计。

  针对问题一，基于开普勒定律，求解着陆准备轨道方程，得嫦娥三号在远月点与近 月点的相应速度。将嫦娥三号的着陆轨道和着陆坐标结合，可求得近月点与月球心的相 对位置，结合椭圆公式可求得远月点坐标。确定了主减速阶段的运动轨迹后，嫦娥三号 的着陆轨迹也就基本确定了。本文在提出燃料最优制导律后，运用四阶 Runge-Kutta 函 数进行分段求解逼近，之后进行神经网络遗传算法寻优。

  针对问题二，通过查阅相关资料，给出了软着陆各个阶段的动力学方程和制导律。 主减速段是耗时最长，燃料消耗最多的阶段，因此采用了燃料最优原则。快速调整阶段 利用推力大小和方向线性变化的制导律，满足主发动机推力和着陆器姿态匀速过渡的要求。粗避障段垂直方向上采用燃料最优原则。为实现粗避障，本文采用对数字高层图进 行分块，计算各块方差后，设置一个合适的阈值，将分块分为安全区和危险区，再利用 动态规划的思想选取最大面积的连续安全区。精避障段同样采取燃料最优原则，并对高 层图进行分块，确定安全区与危险区。为了使最终着陆点与与着陆点接近，采用螺旋前 进搜索方法，搜索与中心点最近的着陆区。缓速下降段主要考虑的是着陆的安全性，故 使用匀变速直线运动模型。

  针对问题三，在对模型的分析与检验中给出相应的误差分析。

关键字： 软着陆 燃料最优控制 Runge-kutta BP 神经网络 遗传算法

一、 问题重述
1.1 背景
实施在月球表面的软着陆是月球勘探计划的重要一步。所谓月球软着陆, 是指着陆 器在制动系统作用下以很小的速度准确降落到月面指定区域, 以保证试验设备和宇航员 的安全。由于月球表面没有大气，因此整个软着陆过程需要制导发动机的控制。正确地 建立着陆器的飞行动力学模型，并在此基础对着陆器的下降轨迹和制导律进行优化设 计，对于着陆器飞行程序的设计和燃料资源消耗等方面具有重要的指导意义。
1.2 需要解决的问题
根据题目信息和附件所示内容, 分析嫦娥三号软着陆过程中的 6 个阶段，研究以下 的问题：
(1) 根据附件 1 与附件 2 研究嫦娥三号的着陆准备轨道，确定该椭圆轨道上近月点 与远月点的位置，以及嫦娥三号相应的速度大小与方向。
(3) 根据问题一和问题二建立的数学模型，对模型进行相应的误差分析和敏感性分 析

二、 模型的假设
• 忽略月球因公转所产生的引力场不均匀;
• 月球自转速度相对缓慢, 忽略自转影响与科里奥利力影响;
• 忽略地球或其他行星对探测器吸引力的影响，只考虑月球对于飞行器的影响作用；
• 因为月球的扁率仅为 1/963.725=0.00308，所以可以将月球简化为球体;
• 因为月球表面没有大气层，几乎无空气阻力，嫦娥三号机械能守恒;
• 嫦娥三号在软着陆全过程不发生意外碰撞和震荡.

三、 符号说明
符号 意义
t0 嫦娥三号进行霍曼下降的初始时刻
t1 嫦娥三号到达近月点的时刻
µ 月球引力常数
r0 远月点的月心距
r1 近月点的月心距
aL 月球半径
h0 远月点轨道高度
h1 近月点轨道高度
v0 嫦娥三号在远月点的速度
v1 嫦娥三号在近月点的速度
vθ0 嫦娥三号在远月点的切向速度
vr0 嫦娥三号在远月点的径向速度
vθ1 嫦娥三号在近月点的切向速度
vr1 嫦娥三号在近月点的径向速度
aF 推力加速度大小
gm 月球引力加速度大小 ℵ 引力与重力方向的夹角 β 速度方向和水平方向的夹角
h 月面高度
h2 粗避障段初始月面高度
h3 粗避障段结束月面高度
th 避障段安全区方差阈值

四、 问题一的模型建立与求解
4.1 问题一分析
从题目信息得，着陆准备轨道为近月点 15km，远月点 100km 的椭圆形轨道。在该 阶段，服从开普勒定律运动，从而可以建立轨道运动方程求解远月点与近月点的速度大 小和方向。
近月点在月心坐标系的位置和软着陆轨道形态共同决定了着陆点的位置，则近月点 的位置可以由着陆点位置和软着陆轨道形态反推得到。主减速阶段结束后，探测器已将 基本处于着陆点正上方，此时探测器的高度也是已知的，因此确定软着陆轨道形态的重 点是确定主减速阶段的运动轨迹。主减速阶段应遵循燃料最优原则，可归类为动态最优 化问题。得到近月点位置后，结合椭圆轨道方程，即可得到远月点位置。
问题一流程图：

4.2 模型的建立 4.2.1 着陆准备轨道的运动学方程
假设嫦娥三号在 t0 时刻在远月点开始霍曼下降，在 t1 时刻到达近月点。在此过程 中的运动学方程 [1] 为: 在 t0 时刻，有：

其中，µ 为月球引力常数，µ=0.4902802627×1013m3/s2;r0 为远月点的月心距；r1 为 近月点的月心距； aL 为月球半径， aL = 1737.013km;h0 为远月点的轨道高度， h0 = 100m； h1 为近月点的轨道高度，h1 = 15km；vθ0 为嫦娥三号在远月点的切向速度; 由于初始时 刻嫦娥三号在远月点，所以初始径向速度 vr0 = 0，v1 为嫦娥三号在远月点的速度。
在 t1 时刻，有：

其中 r1，aL，h0 和 h1 的定义同上，vθ1 是嫦娥三号在近月点的切向速度；由于此时 嫦娥三号在远月点，所以径向速度 vr1 = 0，v1 为嫦娥三号在近月点的速度。
4.2.2 主减速段的动力学方程
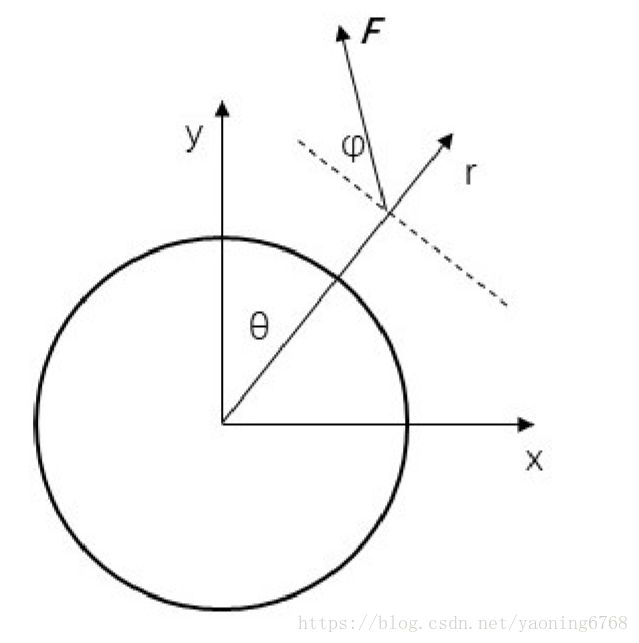
忽略月球自转，则探测器着陆可视为在 19.51W 经度平面上的运动。在此平面建立 坐标系如图所示。近月点的位置可以由着陆点位置和软着陆轨道形态反推得到。主减速 阶段结束后，探测器已将基本处于着陆点正上方，此时探测器的高度也是已知的，因此 确定软着陆轨道形态的重点是确定主减速阶段的运动轨迹。主减速阶段应遵循燃料最优 原则，可归类为动态最优化问题。得到近月点位置后，结合椭圆轨道方程，即可得到远 月点位置。
取月心 o 为坐标原点, 建立直角坐标系 xOy，Oy 由月心指向着陆准备轨道的近月 点;r(θ) 则是以 Oy 轴为起始轴的极坐标系的表达式，r ∈ R+ 为探测器到月心的距离; θ 是 Oy 和 Or 的夹角;ψ 为推力 F 与 Or 夹角的余角；F 为嫦娥三号主减速发动机产生的 推力, 1500 ≤ F ≤ 7500。
在此坐标系下，嫦娥三号质心运动方程可表示为：


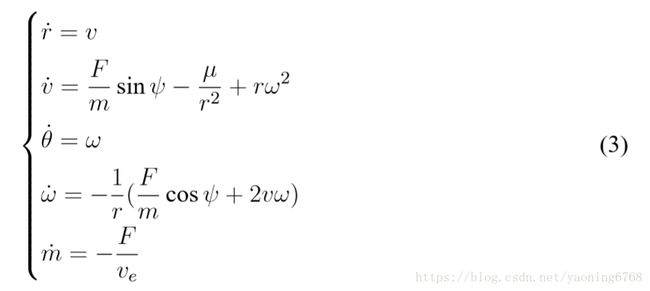
设减速开始的初始时刻 t0 = 0, 主减速阶段结束的时刻为 tf。由嫦娥三号在近月点 的状态可得如下初始条件：

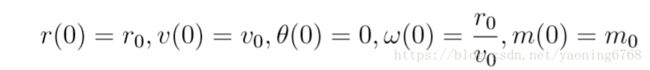
当主减速阶段结束，嫦娥三号到达距月球表面 3km 的高度时，有如下终端条件：

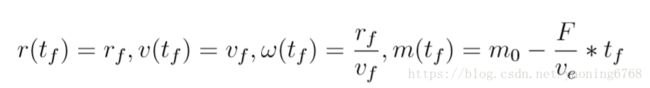
F ve ∗tf 其中，r0 为近月点到月心的距离，v0 为嫦娥三号在近月点的速度，m0 为嫦娥三号在近 月点的质量，rf 为主减速阶段结束时嫦娥三号距离月心的距离，数值上等于月球半径加 3km，vf 为主减速阶段结束时嫦娥三号的速度。
4.2.3 燃料最优控制律设计
将上述动力学模型 (3) 表示成状态方程的形式:

其中，系统状态变量为 x = [r,v,θ,ω,m]T, 控制变量是 u = [F,ψ]T。要求满足燃料最优 制导，取终端性能指标为



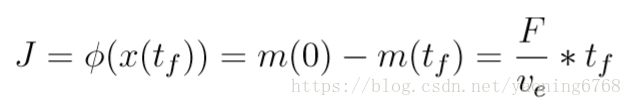
4.2.4 主减速阶段燃料最优控制模型描述
模型的状态方程为 ˙ (x) = f(x,u), 控制变量为 x = [r,v,θ,ω,m]T, 控制变量是 u = [F,ψ]T. 目标函数为：

约束条件有：
1 ⃝嫦娥三号运动状态方程

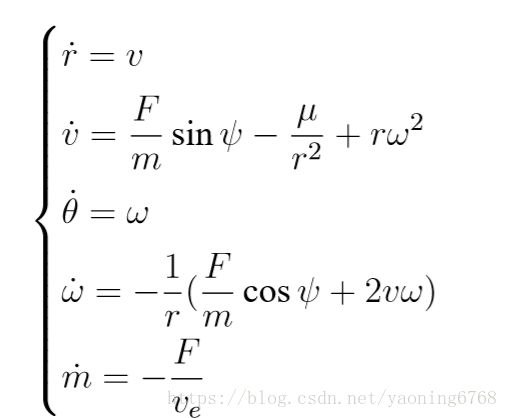
2 ⃝协态变量 λ 满足

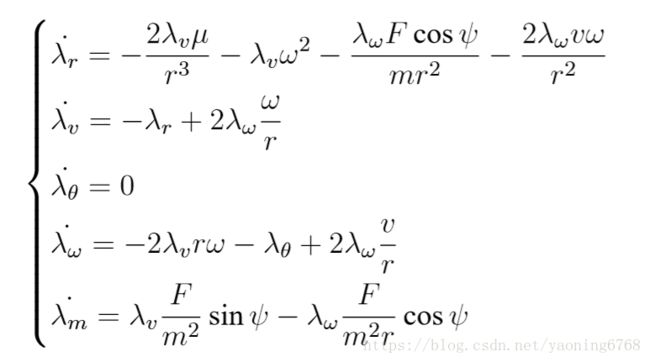
⃝终端条件 G

4.2.5 远月点的位置
嫦娥三号的运行轨道近似一个椭圆，月球则是该椭圆的焦点之一，若设椭圆半长轴 为 a,半短轴为 b,焦点为 c。则焦点(即月球圆心)距离椭圆轨道(即嫦娥三号的绕月轨道) 长轴两端的距离分别为 a+c = 100km,a−c = 15km, 也就是远地点和近地点的高度 (未 减去月球半径)。根据椭圆方程：

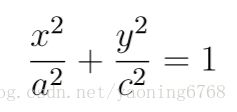
可以求得近月点和远月点的位置关系。

4.3 模型求解 4.3.1 远月点和近月点的速度

4.3.2 燃料最优控制律的求解
最优控制问题的数值方法主要包括直接法和间接法。对于本文提出的燃料最优控制 模型，采用直接参数法进行求解 [3]。查阅相关资料可知，当推力大小可变时，制动期 间发动机一直以最大推力工作最省燃料 [2]，所以此处 F 取恒定值为 7500N；推力方向 角 ψ 可以表示成一个多项式的形式：

在确定了 a0 到 a6 七个变量后，根据前文建立的嫦娥三号运动方程即可确定着陆轨迹。 我们根据神经网络和遗传算法原理，在 MATLAB 中编程实现神经网络遗传算法非线性 函数寻优。
用神BP神经网络表达嫦娥三号的运动状态方程组。即把该方程组看作是一个黑箱， 将 a0 到 a6 七个变量作为输入数据，满足终端条件的 tf 作为输出数据。首先用系统输入 输出数据训练BP神经网络，使网络能够表达该非线性系统，然后就可以用训练好的BP 神经网络预测系统输出。初始的系统训练数据和测试数据由四阶 Runge-Kutta 方法计算 确定。将神经网络输出的预测数据作为遗传算法的适应度值，进行寻优。
(1) 获得初始输入输出数据 为了减少论文计算量，提升神经网络学习效率，减小预测误差，首先我们确定输入 数据 ai,i = 0,1,…,6 的大致范围。根据齐奥尔科夫斯基公式和软着陆初始条件估计，
终端时刻 tf ∈ [400,600] 之间，同时查阅相关资料可知，在主减速阶段结束时，推力的 方向角为 0.64，我们用这两个进行输入数据范围的缩小。从限定范围内随机生成 1000 组数据。
由于对于初始输出数据的获得，我们采用将时间分段的函数逼近法。将 [0,600] 时 间段平均分为 600 段，在每一段内都将 ψ 视为定值。例如在时间分段 [0,1] 内，取 ψ = ψ(0) = a0 + a1 ×0 + a2 ×02 + a3 ×03 + a4 ×04 + a5 ×05 + a6 ×06 = 0, 在 [0,1] 时间分 段内应用四阶 Runge−Kutta 算法对运动学方程 3 进行微分求解，得到 t = 1 时刻的运 动状态描述，再将其作为下一时间分段的初始状态，计算下一时间分段的 ψ 值，不断循 环，直到某一时间分段 [tf,tf + 1] 满足终端条件。通过这种方法，对于每一组特定的输 入值 ai,i = 0,1,…,6，都可以得到一个较为精确的 tf 输出值。
从 1000 组初始输入输出数据中随机选取 800 组作为训练数据，200 组作为测试数 据，并进行归一化处理。

(2)BP 神经网络模拟非线性方程组 用初始数据训练神经网络，是其具有联想和记忆功能。包括以下几个步骤：
1 ⃝BP 神经网络初始化。网络输入节点数为 6，输出结点为 1，根据隐藏结点数选择 经验公式，设置隐藏层结点数为 8。利用随机函数初始化权值和阈值。
2 ⃝BP 神经网络训练。根据输入数据，输入数据与隐含层间的链接权值以及隐含层 的阈值，计算隐含层输出。根据隐含层输出，隐含层与输出层之间的连接权值和输出层 阈值，计算预测输出。根据预测输出以及期望输出之间的误差，更新连接权值和阈值。 重复这一过程，直到迭代结束。
3 ⃝BP 神经网络预测。用训练好的神经网络预测输出。
(3) 遗传算法寻优
遗传算法是一种模拟自然界遗传机制和生物进化论而形成的一种并行随机搜索最 优化方案。它把自然界“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编 码串联群体中，按照所选择的适应度函数并通过遗中的选择、交叉和变异对个体进行筛 选，是适应值好的个体被保留，适应度差的个体被淘汰。包括以下几个步骤： 1 ⃝种群初始化。个体编码方式为浮点数编码，每个个体为一个实数串，由 ai,i = 0,1,…,6 七部分组成。 2 ⃝适应度函数。用上一步训练得到的BP神经网络的预测输出作为适应度值，即BP 神经网络根据输入的 ai,i = 0,1,…,6 预测输出 tf, 适应度值越小越好。 3 ⃝选择操作。本文选择轮盘赌法即基于适应度比例的选择策略，每个个体 i 被选择 的概率 pi 为：

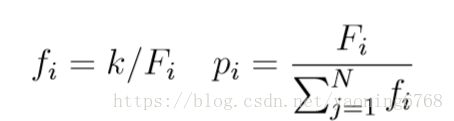
其中，Fi 为个体 i 的适应度值，由于适应度值越小越好，所以在个体被选择前对适应度 求倒数；k 为系数；N 为种群个体数目。
4 ⃝交叉操作。采用实数交叉法。通过对约束条件的分析，可以选择交叉概率为 0.6。
5 ⃝变异操作。通过对约束条件的分析，变异概率为 0.05。 通过计算机仿真模拟，由遗传算法规划出的角度随时间控制函数参数向量的取值 为：
(a0 …a6) = (7.01×10−4 4.30×10−6 −8.12×10−8 6.03×10−10 −1.60×10−12 1.40×10−15)
在此输入下，tf = 413.2s, 水平位移为 385.21km。所以近月点可以是距离着陆点上 空15km，水平距离为385.21km的圆上的任一点。月面上空8km（主减速阶段平均高度） 高度 19.51°W 经线圈的半径为 1743.8km，所以纬度上每变化一度，变化的距离约为每 度 30.43 公里，由水平位移为 385.21km 可得，角度变化为 12.66°
最终结论，近月点位置为19.51°W，31.46°N，距月面15km，速度为1692.53m/s；远 月点位置为 160.49°E，31.46°S，距月面 100km，速度为 1614.215m/s
五、 问题二的建模与求解
5.1 问题二分析
根据附件二资料，嫦娥三号软着陆过程分为六个阶段：着陆准备段，主减速段，快 速调整段，粗避障段，精避障段，缓速下降段。根据每个阶段的不同要求，选择相应的 最优控制策略。
5.2 着陆准备阶段
着陆准备轨道的近月点是15KM，远月点是100KM。在此阶段多采用燃料最优的控 制策略。霍曼转移轨道 4 是一种变换太空船轨道的方法，途中 只需两次引擎推进，相对地节省燃料。问题一中已经给出了相应的动力学模型。
5.3 主减速段
主减速阶段的主要目的是通过推力发动机抵消近月点处较大的初始速度，所以燃料 消耗最优是这一阶段的主要优化目标。问题一中已给出了相应的数学模型。
5.4 快速调整段
快速调整段其介于主减速段和粗避障段之间，其目的主要是调整探测器姿态，使嫦 娥三号平缓地从主减速段过渡到接近段，需要从距离月面 3km 到 2.4km 处将水平速度 减为0m/s。即使主减速发动机的推力竖直向下，之后进入粗避障阶段。为了满足主发动 机推力和着陆器姿态匀速过渡的要求，我们利用推力大小和方向线性变化的制导律，建 立快速调整阶段的推力模型如下所示：

其中制导参数利 k1,k2 用实际的主减速段末端状态和接近段初始状态约束确定。 假设快速调整阶段的初始时刻为 t2，终止时刻为 t3, 本阶段的动力学方程可以将式 (9)、式 (3) 与式 (4) 联立，结合下述初值条件：

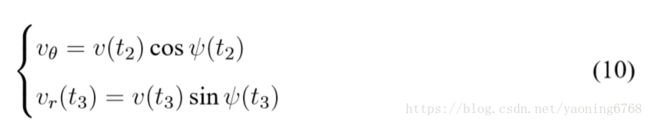
来构造。其中 vθ,vr,v 与前文定义相同。
5.5 粗避障段
粗避障段的范围是距离月面 2.4km 到 100m 区间，其主要是在较大着陆范围内剔除 明显危及着陆安全的大尺度障碍，实现在设计着陆点上方 100m 处悬停，为精避障提供 较好的安全点选择区域。
5.5.1 基于数字高层图的安全区识别算法 附件三中给出了嫦娥三号在距月面 2400m 处对正下方月面 2300×2300m 范围的数 字高程图，该高程图的水平分辨率是 1m/像素，其数值的单位是 1m。例如数字高程图

中第 1 行第 1 列的数值是 102，则表示着陆区域最左上角的高程是 102 米。将图像分为 23×23 个等大方格，每格里面有 100×100 个像素点。计算出每格方差，获得一个 23× 的矩阵。当方差少于一个阈值 th 时，认为该区域是降落安全区，记为 1，否则认为是危 险区，记为 0。
5.5.2 基于动态规划思想的着陆区选择算法
运用上步的模型可以解得一个 01 矩阵。利用动态规划的思想，选取一个包含全是 1 的最大正方形区域，作为着陆区。取其中心为着陆点。
5.5.3 粗避障段的运动学模型
在粗避障阶段，主发动机推力竖直向下。故可以认为主发动机调整竖直方向上的速 度，姿态调整发动机调整水平方向上的速度。 先研究竖直方向上的位移。初始下降速度为快速调整阶段末的速度 v3，末速度为 0m/s。该阶段从 3km 下降到了 100m。 阶段的燃料小韩最小化模型如下：

其中，t4 为此阶段的时间；j 为此段消耗的燃料质量。该试满足以下约束条件：

其中，t 为粗避障阶段中的某一时刻；m 为此时累计消耗的燃料；Fa 此时的推力； s 为此时累计的路程；aF 为此时的加速度；v 为此时刻的速度；am 为此时的合加速度； m4 为进入粗避障阶段时的质量；t4 为粗避障阶段经历的时间；h4 为进入粗避障阶段时 的高度,h6=2400m；h5 为粗避障阶段末的高度，h6=100m。

水平方向上的运动可以看作出末速度为 0m/s 的先匀加速再匀减速直线运动。相应 的运动学方程：

其中 xm 为粗避障段初始位置与与着陆点之间的水平距离，af 为姿态调整发动机提 供的加速度，合成后的轨迹为类似抛物线。
5.5.4 模型求解
用matlab处理数字高层图得到方差矩阵。对比三维图(图4)观察发现，方差在3以 内的格子地势较为平坦。故取阈值 th=3。将方差 Sn

function dYdx = mfunc( x,Y) 
%mfunc 将嫦娥三号的运动方程转化为一阶微分方程组，以便于直接带入ode45函数中进行模拟 
% psi是一个包含七个元素的向量
dYdx(1)= 7.01e-4 + 4.30e-6*2*x -8.12e-8*3*x^2+ 6.03e-10*4*x^3 -1.60e-12*5*x^4+ 1.40e-15*6*x^5; 
dYdx = zeros(6,1); 
f = 7500; mu = 4.9 * 10^12; ve = 2940; 
dYdx(1) = 0.06; dYdx(2) = Y(2); 
dYdx(3) = f / Y(5) * sin(Y(1)) - mu / Y(1)^2 + Y(1) * Y(4)^2; 
dYdx(4) = Y(4); dYdx(5) = -1 / Y(1)*(f / Y(5) * cos(Y(1)) + 2 * Y(2) *Y(4)); 
dYdx(6) = -f / ve; 
end tspan = [0 100]; 
Y0 =[0 1752013 1692.53 9.6605e-4 0 2400]; 
[x,Y] = ode45(@mfunc,tspan,Y0); 
plot(x,Y(:,1),'-o');

附录 B 避障段高层图处理–matlab 源程序

%粗避障段 
%读图像 
A=imread('D:\A\3.tif'); 
%转换为三维图 AA=A; 
if(size(AA,3)>1) 
    AA=rgb2gray(AA); 
end 
AA=double(AA); 
mesh(flipdim(AA,1)); 
%计算方差矩阵 
A1=double(A) M=zeros(23); 
for i=1:23 
    for j=1:23 
            M(i,j)=std2(A1((i-1)*100+1:i*100, (j-1)*100+1:j*100)); 
    end 
end 
%转化为01矩阵 
for i=1:23
    for j=1:23 
        if(M(i,j)<3) 
            MM2(i,j)=1; 
        else 
            MM2(i,j)=0; 
        end 
    end 
end
%导出到txt fid=fopen('D:\A1.txt','w'); 
for i=1:23 
    for j=1:23 
        fprintf(fid,'%2d',MM2(i,j)); 
    end 
    fprintf(fid,'\n');
end 
fclose(fid);
%精避障段 
%读图像 
B=imread('D:\A\4.tif'); 
%转换为三维图 
BB=B; 
if(size(BB,3)>1) 
BB=rgb2gray(BB); 
end 
BB=double(BB); 
mesh(flipdim(BB,1)); 
%计算方差矩阵 
N=zeros(10); 
for i=1:10 
for j=1:10 
N(i,j)=std2(BB((i-1)*100+1:i*100, (j-1)*100+1:j*100)); 
end 
end 
%转化为01矩阵 
for i=1:10 
for j=1:10 
if(N(i,j)<6) 
NN(i,j)=1; 
else NN(i,j)=0; 
end 
end 
end 
%导出到txt fid=fopen('D:\A2.txt','w'); 
for i=1:10
for j=1:10 
fprintf(fid,'%2d',NN(i,j)); 
end 
fprintf(fid,'\n'); 
end 
fclose(fid);

附录 C 动态规划求着陆地区–C++ 源代码

#include  
#include  
using namespace std; 
int main() { 
//读取数据 
ifstream file1("D:\A1.txt",ios::in); short x[23][23]; 
for (int i = 0;i<23;i++) { 
for (int j=0;j<23;j++) { 
file1>>x[i][j];
 } 
 } 
int r=0; 
int dp[23][23]={0}; 
int i,j; 
int mi=1,mj=1; 
for (i = 0; i < 23; i++) 
if (x[i][0] == 1) { 
dp[i][0] = 1; r = 1; 
} 
for (j = 0; j < 23; j++) if (x[0][j] == 1) { dp[0][j] = 1; r = 1; } for (i = 1; i < 23; ++i) { 
for (j = 1; j < 23; j++) {
 if (x[i][j] == 1) { 
 dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1; 
if(r < max(r, dp[i][j])) {
mi=i;mj=j; } 
r = max(r, dp[i][j]); } } } 
cout<<endl; 
cout<<"着陆区边长为"<<r<<"m"<<endl; 
cout<<"其右下角坐标为"<<mi+1<<","<<mj+1; 
system("pause"); }

附录 D 螺旋前进搜索着陆点算法–C++ 源代码

#include  
#include  
using namespace std;
int main() 
{ //读取数据 
ifstream file1("D:\\A2.txt",ios::in); short x[10][10]; 
for (int i = 0;i<10;i++) 
{ 
for (int j=0;j<10;j++) 
{ 
file1>>x[i][j]; 
} 
} 
file1.close();
int m=4,n=4; 
int o=0; while(1) 
{
 o++; 
{ 
if(x[m][n]) 
break; 
n=n+1; 
} 
if(x[m][n]) 
break;
for (int i=2*o-1;i>0;i--) 
{
 if(x[m][n]) break;
} 
if(x[m][n]) break;
for (int i=2*o;i>0;i--)
 { if(x[m][n]) break; n=n-1; } 
 if(x[m][n]) break;
{ if(x[m][n]) 
break; 
m=m-1; }; 
if(x[m][n]) 
break;
} 
cout<<m<<" "<<n; 
system("pause");
}