DPC改进算法--基于共享最近邻和自动确定聚类中心的密度峰值聚类算法
目录
- Fast Searching Density Peak Clustering Algorithm Based on Shared Nearest Neighbor and Adaptive Clustering Center -- Yi Lv, Mandan Liu * and Yue Xiang -- *symmetry*
-
- Abstract
- Introdction
- 本文主要内容
-
- 1, 局部密度ρ的计算方法
- 2,自适应的确定聚类中心
- 3, DPC-SNNACC算法主要流程
- 4,时间复杂度
- 5,部分合成数据集结果可视化
- Conclusion
Fast Searching Density Peak Clustering Algorithm Based on Shared Nearest Neighbor and Adaptive Clustering Center – Yi Lv, Mandan Liu * and Yue Xiang – symmetry
作者命名为DPC-SNNACC算法,顾名思义,在DPC和DPC-SNN中都无法自动确定初始聚类中心(需要人为通过决策图干预),本文提出了一种自动确定聚类中心以及聚类个数。实验结果表明,新提出的DPC-SNNACC算法与DPC算法的三个评价指标类似,但可以避免人主观选取中心点的影响。
Abstract
聚类算法用来在不需要先验知识的情况下揭示数据内在关系然后进一步凭借某一个属性把数据集聚成不同的簇。而DPC以及一部分聚类算法都需要一定的先验知识,18年liu等提出的DPC-SNN算法提出基于共享邻居的相似性度量,在聚类结果较好的情况下仍需要人为干预。基于此,本文作者提出了DPC-SNNACC算法,可以通过决策图来自动的确定“knee point”,进一步不需要人为干预就可以决定聚类中心。首先,提出了一种新的计算局部密度 ρ 的方法;第二,根据决策图来自定确定“knee point”。最后实验结果表明,本文作者提出的算法在聚类效果与DPC-SNN相类似的情况下,还可以自动确定聚类中心。
Introdction
0类似聚类的相关历史在此不赘述,
作者通过列出了传统DPC算法的一些缺点:1,DPC中关于ρ和δ的定义仍需要进行改进以应对具有复杂特征的数据集,例如多密度峰,密度差异大等。2,DPC的分配策略存在多米诺效应,一步错步步皆错。
作者还指出,DPC-SNN算法可以用来弥补一些DPC算法存在的问题,但仍存在一个很明显的问题,即不能自动确定初始聚类中心,仍然需要一定的先验知识。
所以本文的主要创新为:
1, 更新的原算法中关于ρ的定义
2,提出一个新的能通过决策之来自动确定聚类中心的新方法
本文主要内容
作者回顾了前人的对于DPC算法的相关改进算法,并且着重回顾了传统DPC算法和DPC-SNN算法,在此不赘述。
1, 局部密度ρ的计算方法
作者在DPC-SNN的基础上通过改进ρ的定义使得数据点局部密度的差异值进一步扩大。
DPC-SNN计算方式如下:

本文作者采用平方值来进一步放大密度差异:

因为 γ = ρ ∗ δ γ = ρ * δ γ=ρ∗δ ,故放大了局部密度的差异也在一定程度上放大了决策值γ的差异。
2,自适应的确定聚类中心
类似于DPC的假设,我们所要选取做初始聚类中心的点要同时具有较大的ρ和较大的δ值,也就是要具有较大的γ值。
作者先通过平方根函数,将考虑γ的范围从整个数据集缩减到一个较小的范围,再通过计算γ值的变化情况来进一步得到knee point的位置,最后自动确定聚类中心。
主要通过一下公式(14) - (17)来计算:
拐点的位置:
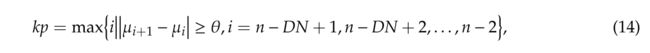
具体的:
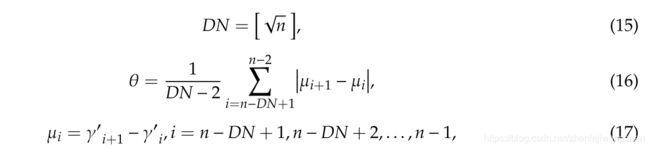
示例:
红线即为knee point所在的位置,位于红线之上的所有点即为我们要确定的聚类中心。(实际算法运行过程中是不需要绘制此图的)
3, DPC-SNNACC算法主要流程
step 1 :初始化数据集X,通过标准化数据集至[0.1]范围内,计算距离矩阵D
step 2 :基于SNN计算相似性度量矩阵
step 3 :基于公式(13)计算局部密度ρ
step 4:计算δ值
step 5:计算γ值,并按升序对γ值进行排列得到 γ ′ γ' γ′
step 6 :根据公式(14)来确定knee point的位置,并得到聚类的个数NC,确定聚类中心集 c e n t e r = c 1 , c 2 , ⋅ ⋅ ⋅ , c C N center = {c_1,c_2,···,c_{CN}} center=c1,c2,⋅⋅⋅,cCN
step 7 :初始化一个队列Q,把所有的中心点并入到Q
以下步骤和DPC-SNN算法的两部分配策略相似
step 8 :取Q的头部作为 x a x_a xa,并寻找 x a x_a xa的所有k最近邻,取集合 K a K_a Ka
step 9 :取 K a K_a Ka里的未分配点 x ′ x' x′,如果 x ′ x' x′满足公式(11),那么便把 x ′ x' x′归为和 x a x_a xa所在的簇,并且把 x ′ x' x′归到Q的末尾;递归下去,再处理下一个 K a K_a Ka中的下一个点;当所有的 K a K_a Ka里的点处理完毕之后,返回step 8,处理下一个Q中的一定从属点。
step 10:当Q变为空集的时候,得到初始聚类结果 Φ ′ = { c 1 , c 2 , . . . , c N C , x p , x p + 1 , . . . } \Phi' = \{c_1,c_2,...,c_{NC},x_p,x_{p+1},...\} Φ′={c1,c2,...,cNC,xp,xp+1,...}
step 11:找到所有未分配的点 x p , x p + 1 , . . . x_p,x_{p+1},... xp,xp+1,...,然后定义一个遍历矩阵M,每一行为未分配的点,每一列代表每一个点的邻居中属于簇的个数。
step 12:找到每一行中的最大值,并且使用最大值所在的簇作为此未分配点所属的簇。遍历下去
step 13:得到最终聚类结果
4,时间复杂度
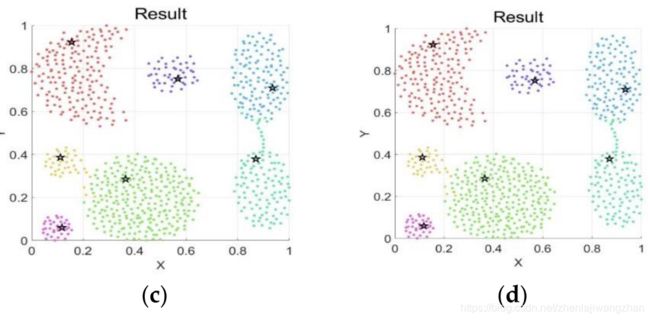
5,部分合成数据集结果可视化
a - kmeans,b - DPC,c - DPC-SNN,d - DPC-SNNACC

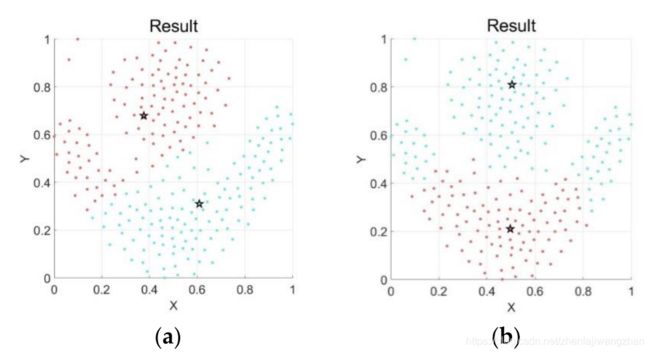
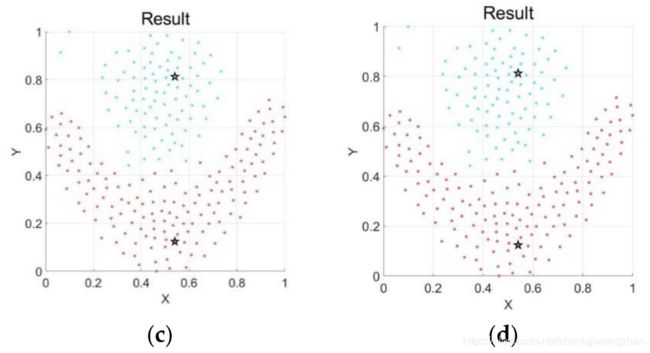
Conclusion
在本篇文章中,为了解决DPC-SNN中需要人为通过决策图确定聚类个数的问题,提出了一个改进算法DPC-SNNACC。首先,通过优化局部密度ρ的计算方式来进一步扩大数据点间的局部密度差异,从而扩大决策值较大的差异。其次,通过计算决策值的差异变化情况提出了一种自动确定knee point的方法。实验结果表明,本文算法在和DPC-SNN算法的效果差不多的情况下可以自动确定初始中心,这是本文最主要的创新。
