代码随想录算法训练营第一天|704. 二分查找 、 27. 移除元素

数组理论基础

数组定义

数组是存放在连续内存空间上的相同类型数据的集合。

数组的内存地址空间

数组下标都是从0开始的，且数组内存空间的地址是连续的。如下图所示，数组通过下标索引获取到下标下对应的数据。
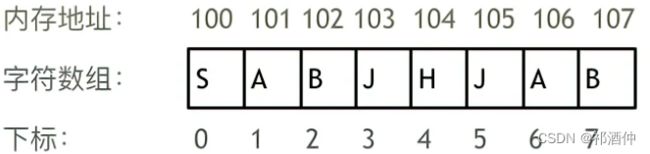（1）因为数组的在内存空间的地址是连续的，所以在增、删元素时，要依次挨个地向前挪位置。
（2）数组的元素的删除并不是真的删除，而是另一个值覆盖上一个值。
注意：（1）如果使用C++，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。
（2）不同编程语言，其内存管理不一样。在C++中二维数组在地址空间上是连续的。而Java没有指针，二维数组在地址空间上不一定是连续的。

704.二分查找

二分搜索法定义

所谓二分搜索法就是在一个数组里找一个target,判断这个target在不在这个数组里面，在的话，返回这个数组里面对应的数组下标，没有搜索到，就返回-1。

二分搜索法易混点

1、while循环时，left与right关系是<还是<=?
2、在缩小区间时，比如左区间的右边界，right是等于middle还是middle-1？
其实，这归根到底是对区间的定义问题，该区间是左闭右闭还是左闭右开。区间的定义不同，会影响到对边界条件的处理

左闭右闭[left,right]

left=0;
right=maxsize-1;
1、循环时，left和right相等的话，区间成立吗？——成立。比如：[1,1]

  |   while（left<=right）

  |   middle = (left + right)/2

2、更新搜索区间时，比如左区间的右边界，right是等于middle还是middle-1？——middle-1 因为缩小区间时，如果middle>target，更新左区间的右边界，区间的定义是左闭右闭，此时的middle一定不是我们搜索的值，接下来的区间就不应该包含这个值，应该是middle-1，下一个搜索区间不应该包含这个已经确定不是target的值。
同理，缩小右区间的左边界时，left=middle+1。

   |   if(nums[middle]

   |   if(nums[middle]>target)
   |       left = middle+1;

左闭右开[left,right)

left=0;
right=maxsize;
1、循环时，left和right相等的话，区间成立吗？——不成立，比如：[1,1)

  |   while（left

  |   middle = (left + right)/2

2、更新搜索区间时，比如左区间的右边界，right是等于middle还是middle-1？——middle 因为缩小区间时，如果middle>target，左闭右开，下一个搜索的左区间不包含middle所在的数值，所以在定义时，应该是right=middle。
更新右区间的左边界，左闭右开，已经明确middle不是target，所以left=middle+1。

   |   if(nums[middle]

   |   if(nums[middle]>target)
   |       left = middle+1;

704.二分查找题目

题目：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

 1 | 输入: nums = [-1,0,3,5,9,12], target = 9     
 2 | 输出: 4       
 3 | 解释: 9 出现在 nums 中并且下标为 4     

示例 2:

 1 | 输入: nums = [-1,0,3,5,9,12], target = 2     
 2 | 输出: -1        
 3 | 解释: 2 不存在 nums 中因此返回 -1        

提示：
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

左闭右闭区间版本

   |   class Solution:
   |       def search(self, nums: List[int], target: int) -> int:
   |     left, right = 0, len(nums) - 1  # 定义target在左闭右闭的区间里，[left, right]
   |
   |    while left <= right:
   |         middle = left + (right - left) // 2
   |         
   |         if nums[middle] > target:
   |            right = middle - 1  # target在左区间，所以[left, middle - 1]
   |        elif nums[middle] < target:
   |            left = middle + 1  # target在右区间，所以[middle + 1, right]
   |         else:
   |             return middle  # 数组中找到目标值，直接返回下标
   |    return -1  # 未找到目标值

左闭右开区间版本

  |   class Solution:
  |     def search(self, nums: List[int], target: int) -> int:
  |          left, right = 0, len(nums)  # 定义target在左闭右开的区间里，即：[left, right)
  |
  |     while left < right: 
  |         middle = left + (right - left) 
  |
  |          if nums[middle] > target:
  |             right = middle  # target 在左区间，在[left, middle)中
  |          elif nums[middle] < target:
  |              left = middle + 1  # target 在右区间，在[middle + 1, right)中
  |          else:
  |              return middle  # 数组中找到目标值，直接返回下标
  |      return -1  # 未找到目标值

27.移除元素

题目来源：力扣（LeetCode）
题目链接：https://leetcode.cn/problems/remove-element

题目：给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1：

   |  输入：nums = [3,2,2,3], val = 3
   |  输出：2, nums = [2,2]
   |  解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

   |  输入：nums = [0,1,2,2,3,0,4,2], val = 2
   |  输出：5, nums = [0,1,4,0,3]
   |  解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

   |  0 <= nums.length <= 100
   |  0 <= nums[i] <= 50
   |  0 <= val <= 100

上面提到，数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

暴力法

两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

   |  class Solution:
   |    def removeElement(self, nums: List[int], val: int) -> int:
   |       i, l = 0, len(nums)
   |       while i < l:
   |          if nums[i] == val: # 找到等于目标值的节点
   |             for j in range(i+1, l): # 移除该元素，并将后面元素向前平移
   |                 nums[j - 1] = nums[j]
   |             l -= 1
   |             i -= 1
   |         i += 1
   |     return l

快慢（双）指针法

通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组。
慢指针：指向更新 新数组下标的位置。

   |   class Solution:
   |      def removeElement(self, nums: List[int], val: int) -> int:
   |          fast = 0  # 快指针
   |           slow = 0  # 慢指针
   |           size = len(nums)
   |           while fast < size:  # 不加等于是因为，a = size 时，nums[a] 会越界
   |        # slow 用来收集不等于 val 的值，如果 fast 对应值不等于 val，则把它与 slow 替换
   |               if nums[fast] != val:
   |                     nums[slow] = nums[fast]
   |                     slow += 1
   |              fast += 1
   |            return slow