第四章 数学知识(三)——高斯消元,组合
文章目录
-
- 高斯消元
- 组合数
-
- 1 <= b <= a <= 2000
- 1 <= b <= a <= 100000
- 1 <= b <= a <= 1 0 18 10^{18} 1018
- 高精度组合数
- 卡特兰数
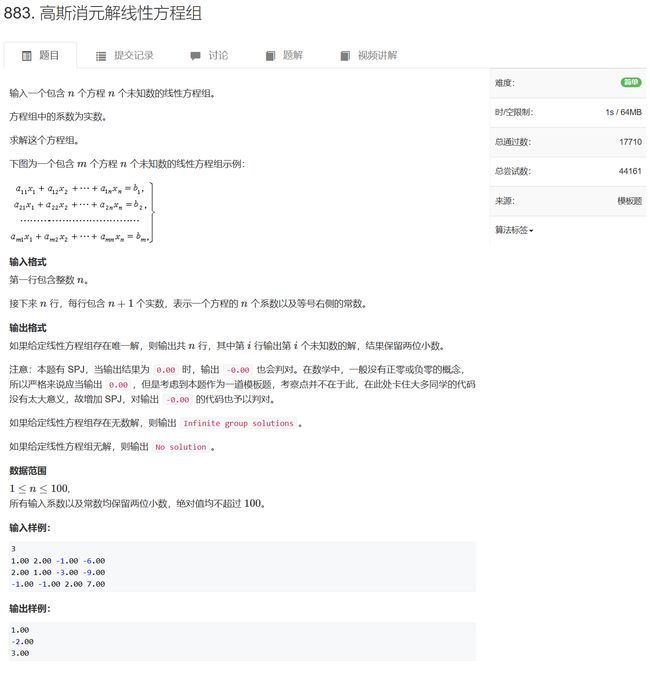
- 高斯消元练习题
-
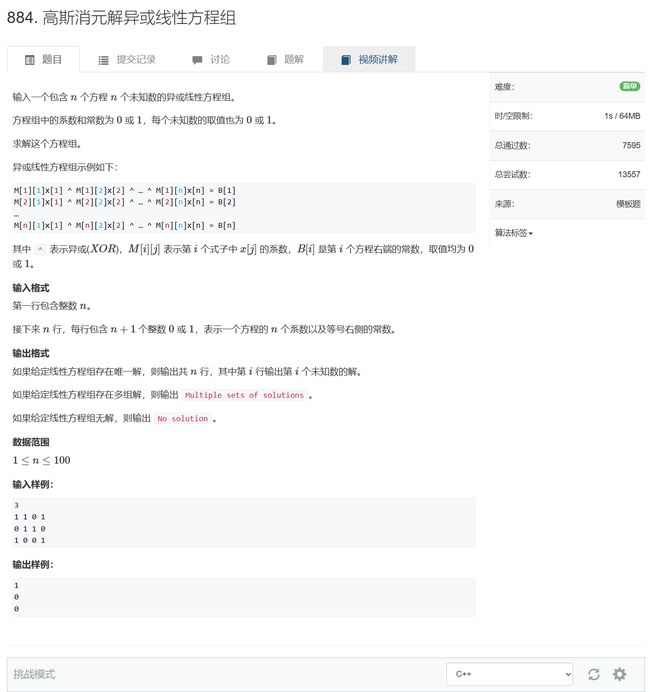
- 884. 高斯消元解异或线性方程组
- 组合数练习题
-
- 885. 求组合数 I
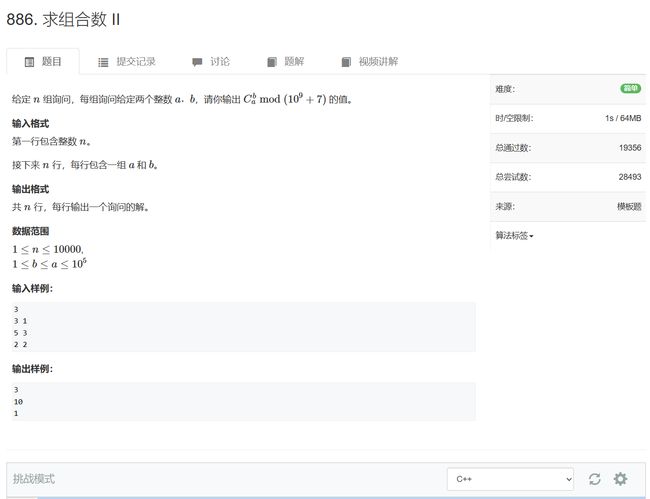
- 886. 求组合数 II
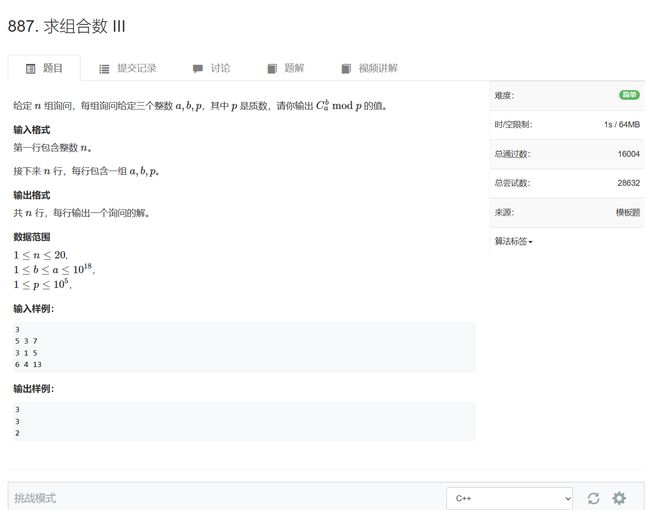
- 887. 求组合数 III
- 888. 求组合数 IV
- 889. 满足条件的01序列
高斯消元
在 n 3 n^3 n3的时间复杂度内求解含有n个未知数的多元线性方程组
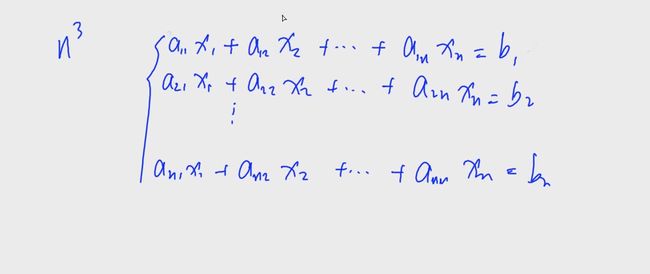
每一个方程表示为:
a i 1 x 1 + a i 2 x 2 + . . . + a i n x n = b i a_{i1}x_1 + a_{i2}x_2+...+a_{in}x_n=b_i ai1x1+ai2x2+...+ainxn=bi
每个方程中有n个未知数,一共有n个这样的方程
方程的解有三种
- 无解
- 唯一解
- 无穷多解
用n * n + 1的系数矩阵表示以上方程组,其中第n + 1列表示 b i b_i bi,对系数矩阵进行初等行变换以解方程,初等行变换有:
- 某一行乘以一个非零的数
- 交换某两行
- 把某行的若干倍加到另一行上
初等行变换前后的方程组是等价的
将矩阵变换成上三角的形式,根据上三角的形式判断解的类型
- 唯一解:完美的阶梯型
- 无解:不是完美阶梯型,方程出现0 = !0的情况
- 无穷多解:不是完美阶梯型,方程出现0 = 0的情况
- 找到当前列中绝对值最大元素所属的行
- 将最大行与当前行交换
- 用初等行变换将当前行的当前列元素变换成1
- 用初等行变换,将当前元素往下的所有元素变换成0(这样的话当前列只有当前元素是非0的)
枚举所有列,每次都进行以上操作。需要注意的是:当最大元素为0时,跳过剩下步骤,直接枚举下一列。若跳过步骤,需要遍历下一列,依然遍历当前行。若完成了所有操作,需要遍历下一列与下一行
若行列式被化简成完美的阶梯型(每次的都是遍历下一列与下一行,即每次找到的最大元素非0),此时需要倒着求解:
矩阵中存储的是每个未知数的系数,每一行第一个未知数的系数都是1,使用初等行变换,只保留每一行的第一个非0系数,将该系数所属列的其他系数都变换成0
0表示无解,1表示唯一解,2表示无穷多解
模板:
int n;
double a[N][N];
const double eps = 1e-8;
// 用r遍历矩阵的行,c遍历矩阵的列,所以r和c表示当前行与当前列
int gauss()
{
for (int c = 0, r = 0; c < n; ++ c )
{
int t = r;
// 找出当前列的最大元素所属的行
for (int i = r + 1; i < n; ++ i ) if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
if (fabs(a[t][c]) < eps) continue;
// 将最大元素所属的行与当前行交换(每个列元素的交换)
for (int j = c; j <= n; ++ j ) swap(a[t][j], a[r][j]);
// 用初等行变换将第一个非0元素变为1
for (int j = n; j >= c; -- j ) a[r][j] /= a[r][c];
// 用初等行变换,使得当前列往下的元素为0
for (int i = r + 1; i < n; ++ i )
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; -- j )
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if (r < n)
{
for (int i = r; i < n; ++ i )
{
if (fabs(a[i][n]) > eps) return 0; // 无解
}
return 2; // 无穷解
}
// 从最后一行开始更新b值
for (int i = n - 1; i >= 0; -- i )
for (int j = i + 1; j < n; ++ j )
a[i][n] -= a[j][n] * a[i][j];
return 1;
}
关于倒着求解:
若最后的矩阵是完美阶梯型,要获取未知数的解,就要使第i行只有第i个元素为1,其他元素都要为0,此时该方程为 x i x_i xi = b i b_i bi
上面的模板中,第一个for之后,对于矩阵的第i行来说,只有前i - 1个元素为0,所以要把第i + 1到最后的元素用初等行变换变为0
由于第i行只有第i个元素为0,所以 a [ i ] [ j ] a[i][j] a[i][j]这个元素要想变成0,只能通过第 j j j行进行初等行变换
因为第j行的第j个元素为1,所以减去第j行的所有元素 * a [ i ] [ j ] a[i][j] a[i][j],就能使 a [ i ] [ j ] a[i][j] a[i][j]为0
必要忘记将第i行的 b i b_i bi值减去第j行的 b j b_j bj * a [ i ] [ j ] a[i][j] a[i][j]
组合数
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab=b!(a−b)!a!
公式中,分母是b!,分子是a * a - 1 * a - 2 * ... * a - b + 1
一个重要的递推式:
C a b = C a − 1 b − 1 + C a − 1 b C_a^b=C_{a-1}^{b-1}+C_{a-1}^b Cab=Ca−1b−1+Ca−1b

可以这么理解:从 a a a个物品中选择 b b b个物品,有几种选法?
从 a a a个物品中随便挑选一个物品,在剩下 a − 1 a-1 a−1个物品中选择 b b b个物品,此时有几种选法?
两种情况:
若选择之前挑好的物品,那么就要在剩下a-1个物品中选择b-1个物品,此时的选法为 C a − 1 b − 1 C_{a-1}^{b-1} Ca−1b−1
若不选择之前挑好的物品,那么就要在剩下a-1个物品中选择b个物品,此时的选法为 C a − 1 b C_{a-1}^b Ca−1b
将这两种情况相加,得到的就是从a个物品中选择b个物品的选法,即 C a b C_a^b Cab
需要注意的是:
从n个物品中选择0个物品,此时的选法 C n 0 C_n^0 Cn0 = 1
从0个物品中选择n个物品,此时的选法 C 0 n C_0^n C0n = 0
根据数据的范围以及精度问题,组合数求解分为4种
1 <= b <= a <= 2000
当题目中的a范围较小,要求该范围内的组合数时,可以直接使用上面的递推公式
C a b = C a − 1 b − 1 + C a − 1 b C_a^b=C_{a-1}^{b-1}+C_{a-1}^b Cab=Ca−1b−1+Ca−1b
将范围内的所有组合数求出并保存,当询问某一组合数时,直接返回
模板:
const int N = 1e9 + 7;
int c[N][N];
for (int i = 0; i < N; ++ i) c[i][0] = 1;
for (int i = 1; i < N; ++ i)
for (int j = 1; j <= i; ++ j)
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
1 <= b <= a <= 100000
根据组合数的定义:
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab=b!(a−b)!a!
对于范围内的数据,先预处理范围内数据的所有阶乘,之后这些阶乘将参与组合数的求解
需要注意的是:0的阶乘为1
当阶乘作为除数时,需要用快速幂求其逆元。为什么不能直接除以阶乘,反而要求其逆元呢?以下程序是两者的对比:
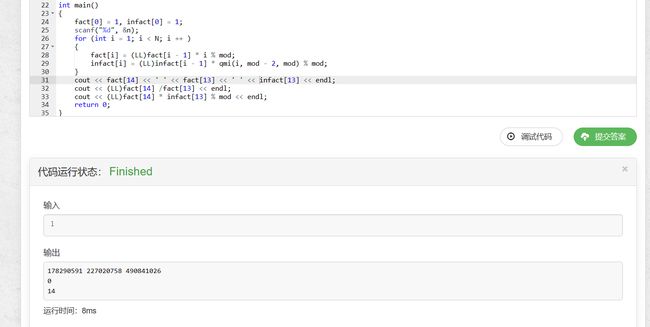
一个直接除以阶乘进行计算,一个乘以其逆元进行计算,只有乘逆元的运算结果是准确的。因为`(a / b) % m != (a % m) / (b % m)
所以我们要预处理两个数组,一个存储范围内数据的阶乘,一个存储阶乘的逆元
模板:
const int N, mod = 1e9 + 7;
int fact[N], infact[N];
fact[0] = 1, infact[0] = 1;
tyepdef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
for (int i = 1; i < N; ++ i )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)qmi(fact[i], mod - 2, mod) % mod;
}
int c = (LL)fact[a] * infact[b] % mod * infact[a - b] % mod;
pritnf("%d\n", c);
1 <= b <= a <= 1 0 18 10^{18} 1018
若p是质数,则有卢卡斯定理:
C a b ≡ C a m o d p b m o d p C a / p b / p ( m o d p ) C_a^b ≡ C_{a\ mod\ p}^{b\ mod\ p}\ C_{a/p}^{b/p}\ (mod\ p) Cab≡Ca mod pb mod p Ca/pb/p (mod p)
若数据范围很大,通过卢卡斯定理,我们就可以将数据缩小到p的范围内
若b / p, a / p还是大于p,那么继续使用卢卡斯定理,代码可以通过递归实现
当数据范围小于p时,直接通过定义求解组合数:
C a b = a ∗ ( a − 1 ) ∗ ( a − 2 ) ∗ . . . ∗ ( a − b + 1 ) b ! C_a^b=\frac{a*(a-1)*(a-2)*...*(a-b+1)}{b!} Cab=b!a∗(a−1)∗(a−2)∗...∗(a−b+1)
模板:
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
if (b > a - b) b = a - b;
int x = 1, y = 1;
for (int i = 0; i < b; ++ i )
{
x = (LL)x * (a - i) % p;
y = (LL)y * (i + 1) % p;
}
return (LL)x * qmi(y, p - 2, p) % p;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
有性质:
C a b = C a a − b C_a^b=C_a^{a - b} Cab=Caa−b
所以当b > a - b时,可以将b = a - b,以减少组合数的计算次数
所以C函数中有if (b - a < b) b = b - a
高精度组合数
分解 C a b C_a^b Cab的质因数,只实现高精度乘法即可
利用组合数的定义:
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab=b!(a−b)!a!
计算 a ! a! a!, b ! b! b!和 ( a − b ) ! (a-b)! (a−b)!中所有质因子的出现次数,将 p i p_i pi在 a ! a! a!中的出现次数减去 p i p_i pi在 b ! b! b!和 ( a − b ) ! (a-b)! (a−b)!中的出现次数相加,就能得到 C a b C_a^b Cab中 p i p_i pi的出现次数k
那么
C a b = p 1 k 1 p 2 k 2 . . . p n k n C_a^b=p_1^{k_1}\ p_2^{k_2}\ ...\ p_n^{k_n} Cab=p1k1 p2k2 ... pnkn
对于 a ! a! a!,如何计算出它的某个质因子 p p p的个数?
a ! = [ a p ] + [ a p 2 ] + [ a p 3 ] + . . . a! = [\frac{a}{p}] + [\frac{a}{p^2}] + [\frac{a}{p^3}] + ... a!=[pa]+[p2a]+[p3a]+...
a ! a! a!由 1 1 1, 2 2 2, 3 3 3, … , a a a这些数相乘,这些数也能分解质因数
若 a a a等于 p p p的 k k k倍(可能有余数),那么在 1 1 1, 2 2 2, 3 3 3, … , a a a这些数中,肯定存在 p p p的 k − 1 k - 1 k−1倍, p p p的 k − 2 k - 2 k−2倍,…, p p p的 1 1 1倍。因为这些数是连续的,这就表示 a ! a! a!中, p p p出现了 k k k次
而某个数等于 p p p的 n n n倍,说明该数的质因数分解中p出现了一次,但 p p p可能会出现2,3,…次,所以还需要判断 p 2 p^2 p2, p 3 p^3 p3,…是否在该数中出现
同样的,通过判断a是 p n p^n pn的几倍,知道 p n p^n pn在 a ! a! a!中出现的次数
再看上面的式子,当 p n > a p^n > a pn>a时,说明 a ! a! a!中不存在 p n p^n pn这个因数,此时计算停止
总结下步骤:
- 线性筛出 a a a的质数
- 求 C a b C_a^b Cab中每个质数的出现次数
- 用高精度乘法将所有的质因数乘到一起得到 C a b C_a^b Cab
模板:
int primes[N], cnt;
bool st[N];
int pcnt[N];
void get_primes(int n)
{
for (int i = 2; i <= n; ++ i )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= i / j; ++ j )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
// 获取a!中质因数p的个数
int get(int a, int p)
{
int res = 0;
while (a)
{
res += a / p;
a /= p;
}
return res;
}
vector<int> mul(vector<int>& a, int b)
{
vector<int> c;
int t = 0, s = a.size();
for (int i = 0; i < s || t; ++ i )
{
if (i < s) t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
return c;
}
get_primes(a);
// 计算a!,b!和(a - b)!中,所有质数的出现次数并存储在pcnt中
for (int i = 0; i < cnt; ++ i )
{
int p = primes[i];
pcnt[i] = get(a, p) - get(b, p) - get(a - b, p);
}
// 将所有质因数相乘得到最后的答案
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; ++ i )
for (int j = 0; j < pcnt[i]; ++ j )
res = mul(res, primes[i]);
for (int i = res.size() - 1; i >= 0; -- i )
printf("%d", res[i]);
printf("\n");
卡特兰数
直接看题:
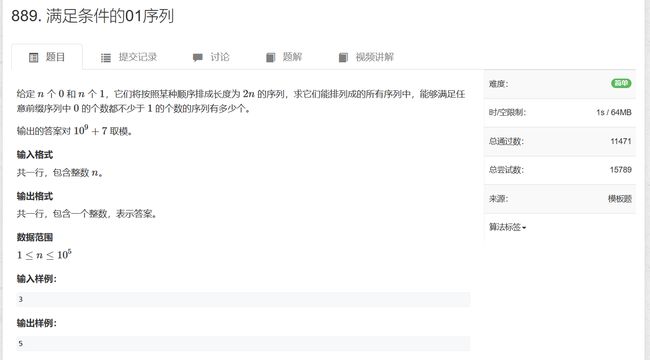
01序列可以转换成矩阵中的路径问题
0表示向右走一步,1表示向上走一步
题目给定n个0和n个1,我们就可以从(0, 0)开始走,最后走到(n, n)这个点
可以走几步?从2n步中选择n步向上或向右走,总共的步数就是 C 2 n n C_{2n}^n C2nn
转换题目的限制条件:任意前缀中0的数量都要大于等于1的数量
也就是在坐标中x >= y,路径只能接触下图中的绿线并且位于绿线下方
当路径中的某个点接触到了红线,就说明该路径是一条不符合题目要求的路径
找出所有不符合题目要求的路径,将总的路径数减去不符合题意的路径数,就能得到我们想要的答案
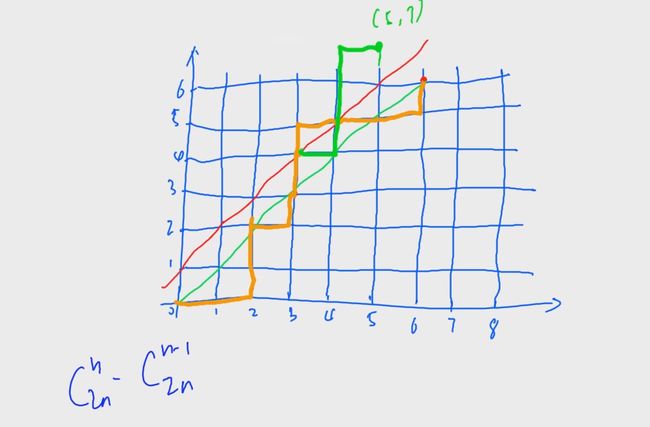
现在的问题是不符合题意的路径有几条?
假设一条路径接触或越过了红线,我们将这条路径中第一次与红线接触的点往后的路径,以红线为对称轴做轴对称
我们能发现所有不符合题意的路径最后都递达了(n - 1, n + 1)这个点
所以不符合题意的路径数为:从(0, 0)开始到(n - 1, n + 1)这个点的路径数,也就是 C 2 n n − 1 C_{2n}^{n-1} C2nn−1
所以符合题意的路径数为:
C 2 n n − C 2 n n − 1 C_{2n}^n - C_{2n}^{n-1} C2nn−C2nn−1
将其化简得到:
C 2 n n n + 1 \frac{C_{2n}^n}{n+1} n+1C2nn
该数被称为卡特兰数
如何求解卡特兰数?根据数据范围从四种求组合数的方式种选择一种适合的即可
高斯消元练习题
#include debug:eps定义成int类型,应该定义成double类型,这是第二次犯了
倒着求解时,i应该等于r
fabs要记得加,老是忘
884. 高斯消元解异或线性方程组
就是高斯消元的简单变形,初等行变换用异或体现就行了
#include debug:
for (int i = r; i <= n; ++ i )
{
if (a[i][c])
{
t = i;
break;
}
}
t = i写成t = r
最后倒着求答案时
a[i][n + 1] ^= a[j][n + 1]写成a[i][n + 1] ^= a[j][n + i],?这谁找得到啊
组合数练习题
885. 求组合数 I
#include 886. 求组合数 II
#include 887. 求组合数 III
#include debug:有一个乘法运算没有LL的强转,导致爆int,最后出现负数
所以每次的乘法都要检查是否有LL的强转以及模p
888. 求组合数 IV
#include 889. 满足条件的01序列
由于这道题的数据范围在10000以内,所以直接根据定义求组合数即可
#include