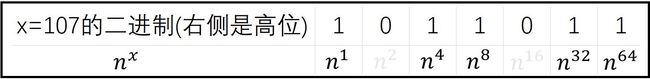数学相关算法

欢迎访问我的博客首页。

---

1. 整数划分

---

1.1 整数的所有划分

---

  题目来自 牛客。
  使用分治算法的回溯版本：

class Solution {
public:
	vector<vector<int>> integerBreak(int n) {
		if (n < 1)
			return {};
			
		vector<vector<int>> res;
		DAC(n, res);
		return res;
	}
private:
	void DAC(int n, vector<vector<int>>& res, vector<int>& yi = vector<int>{}) {
		if (n < 0)
			return;
		if (n == 0) {
			res.push_back(yi);
			return;
		}
		
		for (int i = 1; i <= n; i++) {
			yi.push_back(i);
			DAC(n - i, res, yi);
			yi.pop_back();
		}
	}
};

  从第 22 行的第一个参数可以看出，递归调用时 DAC 函数的第一个参数不会小于 0。按照这个算法，3 的划分即包括 {1,2} 也包括 {2,1}。

1.2 整数的 m 划分

---

  把一个正整数 n 拆分成若干个不小于1且不大于 n 的整数相加的形式，对 n 进行一次拆分得到的这些数称为 n 的一个划分。即 n = x1 + x2 + … + xk，1 ≤ xi ≤ n 且 xi 是整数，则称 x1, x2, …, xk 是 n 的一个划分。如果一次拆分得到的数最大值不大于 m，称这个划分是 n 的一个 m 划分。给定 n 和 m，求 n 有多少种 m 划分。

  分析：假设 n 的 m 划分有 f(n, m) 种。我们可以把这 f(n, m) 种划分分成两类：把划分后含有 m 这个数的所有划分称为第一类，剩下的称为第二类。
  很明显，第二类的每个划分中的数都不大于 m - 1，所以第二类的划分数是 f(n, m - 1)。对于第一类，因为每个划分都包含 m 这个数，所以相当于对 n - m 这个数进行 m 划分，于是第一类的划分数是 f(n - m, m)。所以总的划分数 f(n, m) = f(n, m - 1) + f(n - m, m)。

1. 分治算法

size_t DAC(int n, int m) {
	if (n < 1 || m < 1) return 0;
	if (n == 1 || m == 1) return 1;
	if (n < m) return DAC(n, n);
	if (n == m) return DAC(n, m - 1) + 1;
	return DAC(n, m - 1) + DAC(n - m, m);
}

2. 动态规划

  上面的分治算法对应的动态规划算法如下。

size_t dp(int n, int m) {
	int dp[6][4]; // int dp[n+1][m+1]。dp[i][j]=x：i的j划分有x种。
	memset(dp, 0, sizeof(dp));
	for (int i = 1; i <= n; i++) {
		dp[i][1] = 1;
		for (int j = 1; j <= m; j++) {
			dp[1][j] = 1;
			if (i < j)
				dp[i][j] = dp[i][i];
			else if (i == j)
				dp[i][j] = dp[i][j - 1] + 1;
			else
				dp[i][j] = dp[i][j - 1] + dp[i - j][j];
		}
	}
	return dp[n][m];
}

1.3 整数划分的最大积

---

  题目来自 《LeetCode 343.整数拆分》、AcWing。相同题目《剑指 Offer 第二版 14.剪绳子》。

  先用分治算法穷举所有情况。

class Solution {
public:
	int integerBreak(int n) {
		if (n < 1)
			return 0;
		if (n < 4)
			return n - 1;
			
		int res = 1;
		DAC(n, res);
		return res;
	}
private:
	void DAC(int n, int& res, int yi = 1) {
		if (n == 0) {
			res = max(res, yi);
			return;
		}

		for (int i = 1; i <= n; i++) {
			yi *= i;
			DAC(n - i, res, yi);
			yi /= i;
		}
	}
};

  本题只求最大积，并没有让输出所有划分，所以使用分治算法不划算，应该使用动态规划算法。
  我们以 n = 2 开始计算几次就会发现，n = 2 和 n = 3 比较特殊。从 n = 4 开始的推导过程应该是这样的：dp[4] = dp[2] * dp[2] = 4, dp[5] = dp[2] * dp[3] = 6，…。我们会发现，按照这样的推导，dp[2] 应该是 2，dp[3] 应该是 3。这样就可以使用动态规划了。

class Solution {
public:
	int integerBreak(int n) {
		if (n < 1)
			return 0;
		if (n < 4)
			return n - 1;

		return DP(n);
	}
private:
	int DP(int n) {
		int *dp = new int[n + 1];
		// 1.dp[2:3]。
		dp[2] = 2, dp[3] = 3;
		// 2.dp[4:n] = 0, 因为下面要找最大值。
		memset(dp + 4, 0, sizeof(int) * (n + 1 - 4));
		// 3.dp[4:n]。
		for (int i = 4; i <= n; i++) {
			for (int j = 2; j <= i - 2; j++) {
				dp[i] = max(dp[i], dp[j] * dp[i - j]);  // j * dp[i - j];
			}
		}
		int res = dp[n];
		delete[] dp;
		return res;
	}
};

  递推公式可以是 dp[i] = max(dp[i], dp[j] * dp[i - j])，也可以是 dp[i] = max(dp[i], j * dp[i - j])。前者是把大问题划分成两个小的子问题，后者是把大问题划分成一个子问题与一个加数。
  从上面的分析可以看出，从 n = 4 开始，乘积最大的划分方法是：尽可能多地划分出不3，剩余的数只能是 2。所以本题可以使用时间复杂度和空间复杂度都是 O(1) 的算法解决。

class Solution {
public:
	int integerBreak(int n) {	
		// 1.无效的输入。
		if (n < 2)
			return 0;
			
		// 2.两个最小问题的解比较特殊。
		if (n < 4)
			return n - 1;
		// 3.尽可能多地划分出3，剩余的划分出 2。
		int num_of_3 = n / 3;
		int residue = n - 3 * num_of_3;
		if (residue == 0)
			return pow(3, num_of_3);
		else if (residue == 1)
			return pow(3, num_of_3 - 1) * 2 * 2;
		else //if (residue == 2)
			return pow(3, num_of_3) * 2;
	}
};	

2. 快速求幂

---

  题目来自《LeetCode 50.Pow(x, n)》。底数可以是小数，取值范围是 -100.0 < x < 100.0。指数可以是正整数、负整数和零，取值范围是 $-2^{31}<=n<=2^{31}-1$。

  如上图所示，快速求 $n^x$ 就是求 x 的二进制数的每一位，同时求 n 的平方、求 n 的平方的平方… 但只把二进制数位上的数为 1 时对应的平方结果累乘，如上图第二行除灰色字体外的黑体部分。

class Solution {
public:
	double myPow(double x, int n) {
		if (x == 0)
			return 0;
		if (n == 0)
			return 1;

		if (n < 0) {
			long long temp = n;
			return 1.0 / pow(x, -1 * temp);
		}
		return pow(x, n);
	}
private:
	double pow(double x, long long n) {
		double res = 1, square = x;
		while (n != 0) {
			if (n % 2 == 1) {
				res *= square;
			}
			n /= 2;
			square = square * square;
		}
		return res;
	}
};

  因为指数可以取到最小的 32 位整数，所以求它的绝对值时不能直接乘 -1。顺便说一下高效判断奇偶的方法：奇数&1 = 1/true，偶数&1 = 0/false，任何数&0 = 0。

3. 两数相除

---

  题目来自《LeetCode 29.两数相除》，利用快速减法求商。

4. 完全平方数

---

  题目来自《LeetCode 279.完全平方数》。
  顺便指出，每个正整数都可以可以拆分成 n 个平方数相加的形式，且 n ≤ 4。

class Solution {
public:
	int numSquares(int n) {
		if (n < 0)
			return 0;
			
		int *dp = new int[n + 1];
		// 1.最小子问题的解。
		dp[0] = dp[1] = 1;
		// 2.为求最小值做准备。
		for (int i = 2; i <= n; i++)
			dp[i] = INT_MAX;
		// 3.求更大的问题。
		for (int i = 2; i <= n; i++) {
			for (int j = 1; j < i; j++) {
				if (i - pow(floor(sqrt(i)), 2) == 0)
					dp[i] = 1;
				else
					dp[i] = min(dp[i], dp[j] + dp[i - j]);
			}
		}
		int res = dp[n];
		delete[] dp;
		return res;
	}
};

  上面的算法在力扣第 548/588 个测试数据 6366 上超出时间限制。

class Solution {
public:
	int numSquares(int n) {
		if (n < 0)
			return 0;
		if (n == 0)
			return 1;
			
		int* dp = new int[n + 1];
		// 1.递推的基础。
		dp[0] = 0;
		// 2.为求最小值做准备。
		for (int i = 1; i <= n; i++)
			dp[i] = INT_MAX;
		// 3.求解更大的问题。
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= sqrt(i); j++) {
				dp[i] = min(dp[i], dp[i - j * j] + 1);
			}
		}
		int res = dp[n];
		delete[] dp;
		return res;
	}
};

5. 字符串相乘

---

  题目来自《LeetCode 43.字符串相乘》，求大数相乘。

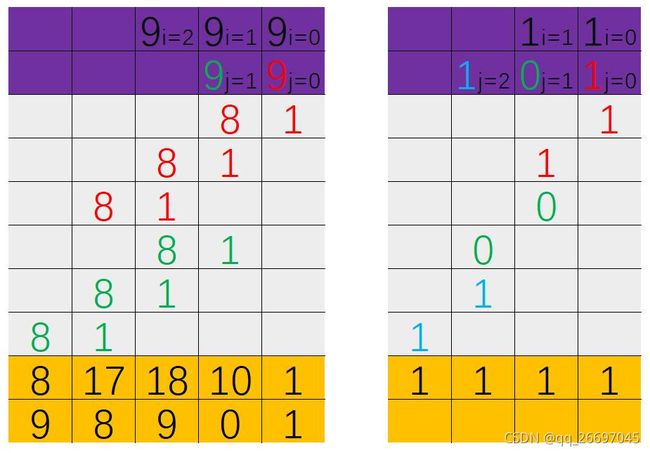
  假如字符串下标 0 处存放的是最低位。被乘数和乘数的任意一位 multiplicand[i] = a 和 multiplier[j] = b 相乘，实际是 $a\times 10^i$ 与 $b\times 10^j$ 相乘。乘积 $c=a\times b$ 实际是 $c\times 10^{i+j}$，c 前面有 i + j 个 0。于是， c 在乘积字符串中的下标是 i + j， 所以 product[i + j] = c % 10，进位放在更高一位 product[i + j + 1] = c / 10。
  根据上面的分析，m 位的被乘数与 n 位的乘数的乘积最多有 m + n 位，最少有 m + n - 1 位。所以我们要申请长度为 m + n 的数组存放乘积。
  假如字符串下标 0 处存放的是最高位，被乘数有 m 位，乘数有 n 位，乘积存放在长度为 m + n 的字符串中。被乘数和乘数的任意一位 multiplicand[i] = a 和 multiplier[j] = b 相乘，实际是 $a\times 10^{m-1-i}$ 与 $b\times 10^{n-1-j}$ 相乘。乘积 $c=a\times b$ 实际是 $c\times 10^{m+n-2-i-j}$，c 后面有 m + n - 2 - i - j 个 0。于是， c 在乘积字符串中的下标是 (m + n) - (m + n - 2 - i - j) = i + j + 1， 所以 product[i + j + 1] = c % 10，进位放在更高一位 product[i + j] = c / 10。

class Solution {
public:
	string multiply(string num1, string num2) {
		if (num1.size() == 0 || num2.size() == 0)
			return "";
			
		int m = num1.size(), n = num2.size();
		string product(m + n, '0');
		// 1.逐位相乘。
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				int temp = (num1[i] - '0') * (num2[j] - '0');
				product[i + j + 1] += temp % 10;
				product[i + j] += temp / 10;
				// 2.及时处理进位以避免越界。
				add_carry(product, i + j + 1);
			}
		}
		// 3.去除前部的'0'。
		int begin;
		for (begin = 0; begin < product.size(); begin++)
			if (product[begin] != '0')
				break;
		// 4.被乘数或乘数可能是全'0'。
		if (begin == product.size())
			return "0";
		return product.substr(begin);
	}
private:
	void add_carry(string& product, int end) {
		if (end < 0)
			return;
			
		end = min(end, (int)product.size() - 1);
		int temp, x, carry = 0;
		for (int i = end; i >= 0; i--) {
			temp = product[i] - '0' + carry;
			x = temp % 10;
			carry = temp / 10;
			product[i] = '0' + x;
		}
	}
};

6. 参考

---

1. 完全平方数， CSDN
2. 完全平方数，CSDN
3. 取余运算定律，CSDN