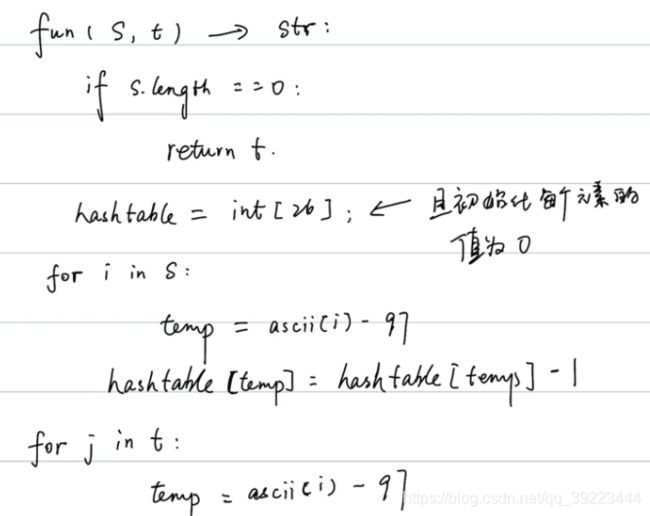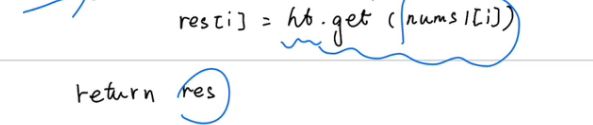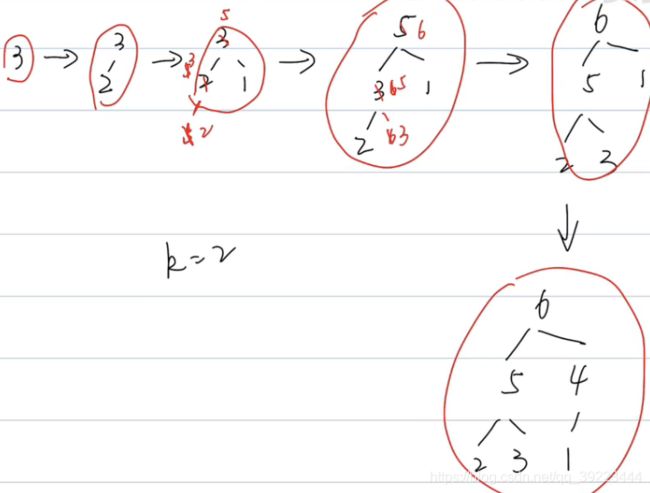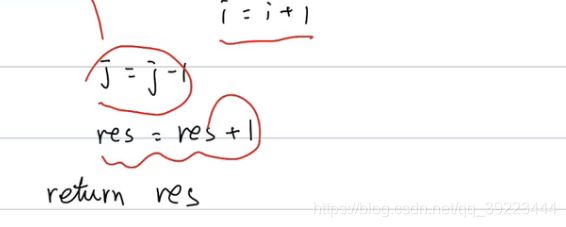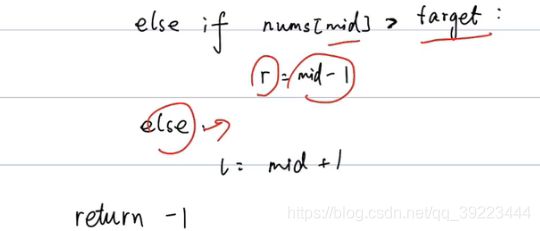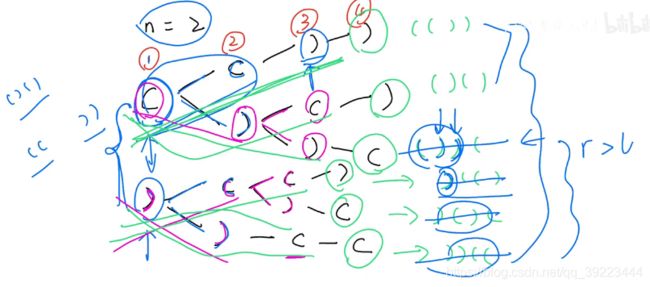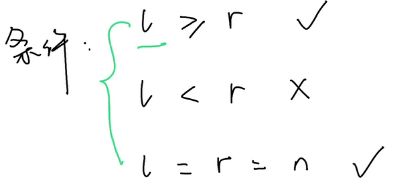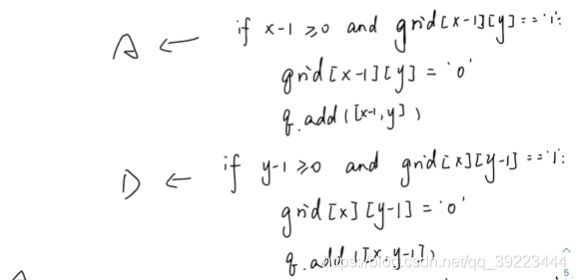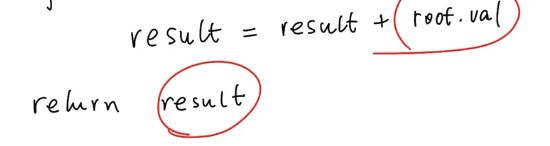手把手带你刷Leetcode力扣 学习总结
文章目录
- 1. 总体规划
- 2. 算法复杂度
-
- 2.1 时间复杂度
- 2.2 空间复杂度
- 3. 数据结构
-
- 线性表
- 3.1 数组【Array】
-
- 3.1.1 Python常用操作
- 3.1.2优缺点
- 3.1.3 练习题
-
- 485 最大连续1的个数
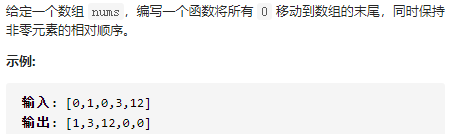
- 283 移动零
- 27 移除元素
- 3.2 链表【Linked List】
-
- 3.2.1 Python常用操作
- 3.2.2 Java常用操作
- 3.2.3 练习题
-
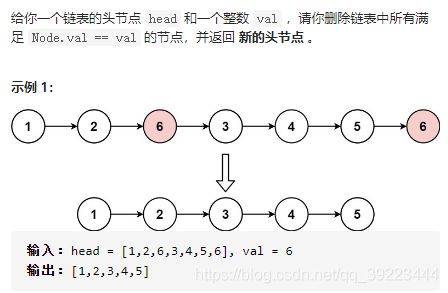
- 203 移除链表元素
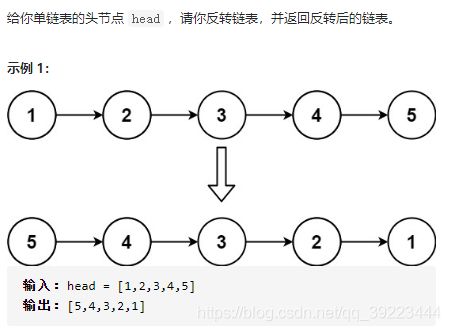
- 206 反转链表
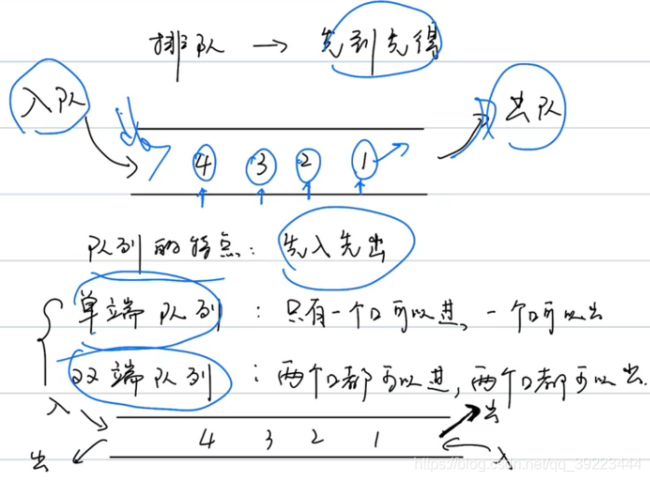
- 3.3 队列【Queue】
-
- 3.3.1 Python常用操作
- 3.3.2 Java常用操作
- 3.3.3 练习题
-
- 933 最近的请求次数
- 3.4 栈【Stack】
-
- 3.4.1 Python常用操作
- 3.4.2 Java常用操作
- 3.4.3 练习题
-
- 20 有效的括号
- 1614 括号的最大嵌套深度
- 496 下一个更大元素(栈+队列)
- 3.5 哈希表【Hash Table】
-
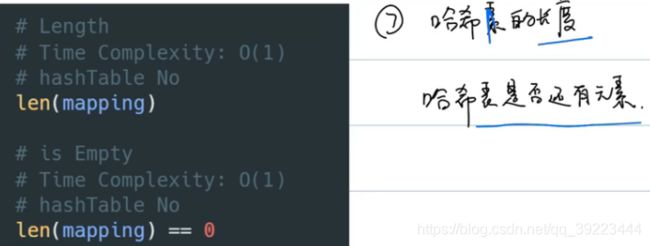
- 3.5.1 Python常用操作
- 3.5.2 Java常用操作
- 3.5.3 练习题
-
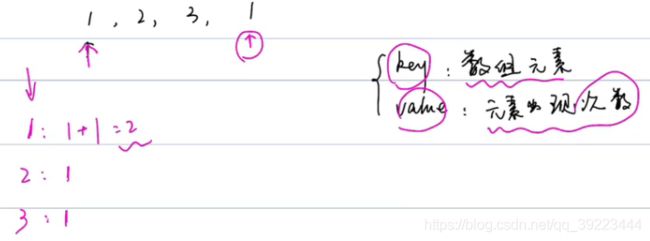
- 217 存在重复元素
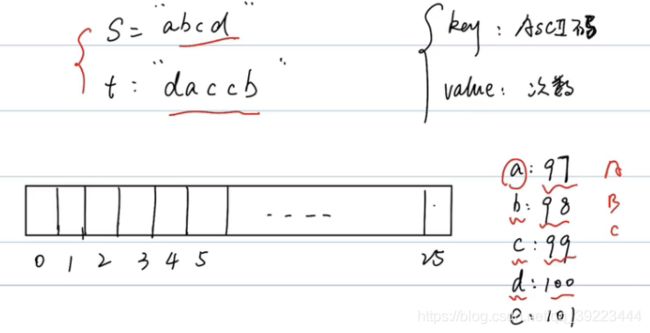
- 389 找不同
- 496 下一个更大元素
- 3.6 集合【Set】
-
- 3.6.1 Python常用操作
- 3.6.2 Java常用操作
- 3.6.3 练习题
-
- 217 存在重复元素
- 705 设计哈希集合
- 3.7 树【Tree】
-
- 练习题
-
- 144
- 94
- 145
- 3.8 堆【Heap】
-
- 3.8.1 Python常用操作
- 3.8.2 Java常用操作
- 3.8.3 练习题
-
- 215 数组中第k个最大元素
- 692 前k个高频单词
- 3.9 图【Graph】
- 3.10 前缀树|字典树【Trie】
-
- 练习题
-
- * 208 Implent Trie 实现Trie[模版]
- 720
- 692
- 3.11 数据结构知识点回顾
- 4. 算法
-
- 4.1 双指针
-
- 4.1.1 算法
- 4.1.2 练习题
-
- 141 环形链表
- 881 救生艇
- 4.2 二分查找
-
- 4.2.1 算法
- 4.2.2 练习题
-
- 704 二分查找
- 35 搜索插入位置
- 162 寻找峰值
- 74 搜索二维矩阵
- 4.3 滑动窗口(技巧)
-
- 4.3.1 算法
- 4.3.2 练习题
-
- 209 长度最小的子数组
- 1456 定长子串中元音的最大数组
- 4.4 递归 recursion
-
- 4.4.1 算法
-
- 什么样的问题可以用递归解决呢?
- 如何实现递归
- 4.4.2 练习题
-
- 509 斐波那契数列
- 206 反转链表
- 344 反转字符串
- 4.5 分治法(divide & conquer)
-
- 4.5.1 算法
- 4.5.2 练习题
-
- 169 多数元素
- 53 最大子序列
- 4.6 回溯法(Backtracking)
-
- 4.6.1 算法
- 4.6.2 练习题
-
- 22 括号生成
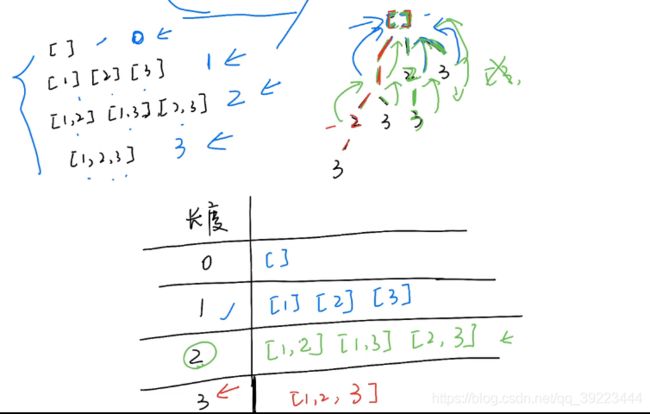
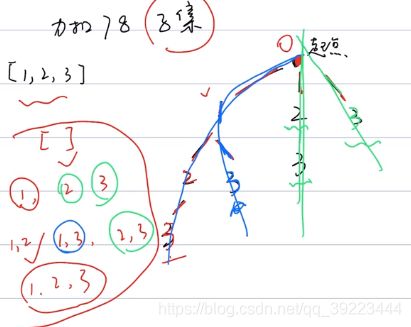
- 78 子集
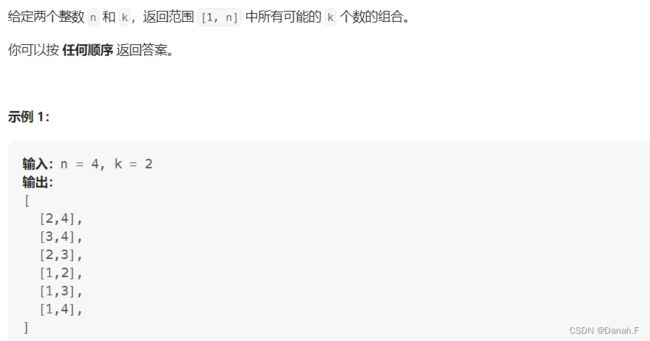
- 77 组合
- 46 全排列
- 华为OD 组装新的数组
- 51 N皇后
- 36 有效的数独
- 4.7 深度优先搜索(DFS)
-
- 4.7.1 算法
- 4.7.2 练习题
-
- 938 二叉搜索树的范围和
- 78 子集
- 200 岛屿数量
- 4.8 广度优先搜索(BFS)
-
- 4.8.1 算法
- 4.8.2 练习题
-
- 938 二叉搜索树的范围和
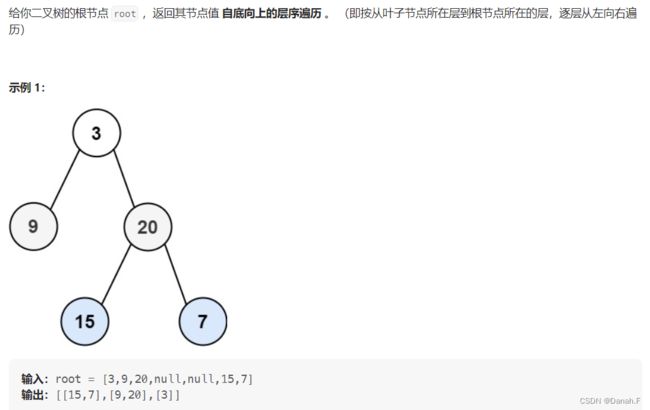
- 102 二叉树的层序遍历
- 107 二叉树的层序遍历II
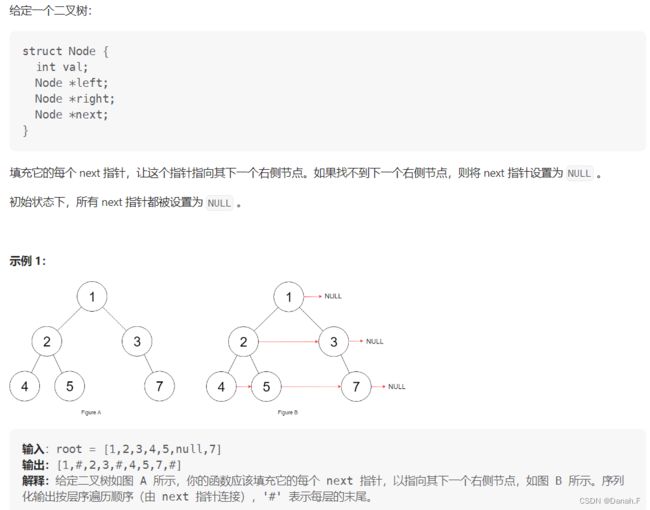
- 117 填充每个节点的下一个右侧节点指针II
- 655 输出二叉树
- 662 二叉树最大宽度
- 4.9 动态规划
-
- 4.9.1 算法
- 4.9.2 练习题
-
- 509 斐波那契数列
- 62 不同路径
- 121 买卖股票的最佳时机
- 122 买卖股票的最佳时机II
- 123 买卖股票的最佳时机III
- 188 买卖股票的最佳时机IV
- 309 最佳买卖股票实际含冷冻期
- 714 买卖股票的最佳时机含手续费
- 70 爬楼梯
- 279 完全平方数
- 221 最大正方形
- 4.10 查找
-
- 4.10.1 常见查找算法
-
- 4.10.1.1 算法
- 4.10.1.2 练习题
- 4.11 排序
-
- 4.11.1 常见排序算法
-
- 4.11.1.1 时间复杂度
- 4.11.1.2 如何分析一个排序算法
- 4.11.2 冒泡排序
-
- 4.11.2.1 算法
- 4.11.2.2 练习题
- 4.11.3 选择排序
-
- 4.11.3.1 算法
- 4.11.3.2 练习题
- 4.11.4 插入排序
-
- 4.11.4.1 算法
- 4.11.4.2 练习题
- 4.11.5 希尔排序
-
- 4.11.5.1 算法
- 4.11.5.2 练习题
- 4.11.6 归并排序
-
- 4.11.6.1 算法
- 4.11.6.2 练习题
- 4.11.7 快速排序
-
- 4.11.7.1 算法
- 4.11.7.2 练习题
- 4.11.8 堆排序
-
- 4.11.8.1 算法
- 4.11.8.2 练习题
- 4.12 查找算法
-
- 4.12.1 顺序查找
-
- 4.12.1.1 算法
- 4.12.1.2 练习题
- 4.12.2 二分查找
-
- 4.12.2.1 算法
- 4.12.2.2 练习题
- 4.12.3 插值查找
-
- 4.12.3.1 算法
- 4.12.3.2 练习题
- 4.13 贪心算法
-
- 4.13.1 算法
- 4.13.2 例题
-
- 322 零钱兑换
- 1217 玩筹码
- 55 跳跃游戏
- 华为od 最大利润、贪心的商人
- 4.14 其他
-
- HJ28 素数伴侣
- HJ108 最小公倍数
- HJ25 数据分类处理
- 计数质数
- NC61 两数之和
- 合并区间
- 华为od 最大版本号
UP讲的很好,推荐大家去看。
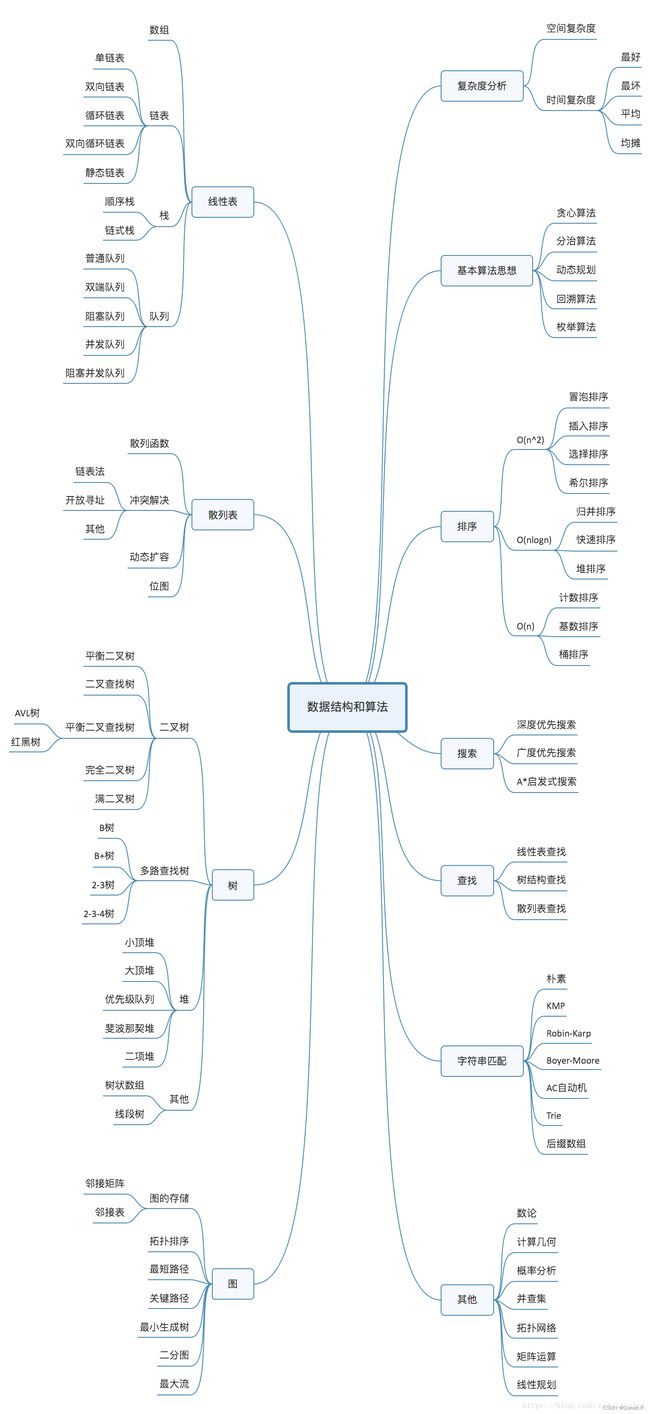
1. 总体规划
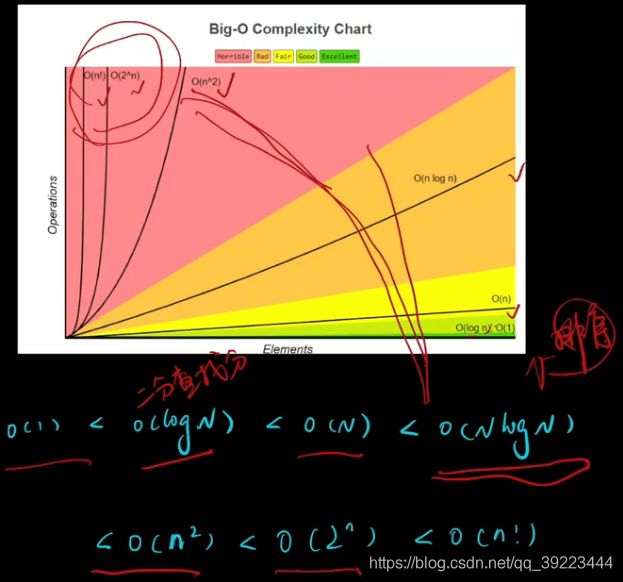
2. 算法复杂度
复杂度分析法则:
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
2.1 时间复杂度
-
时间复杂度分析
只关注循环执行次数最多的一段代码
加法法则:总复杂度等于量级最大的那段代码的复杂度
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积 -
常见时间复杂度案例分析

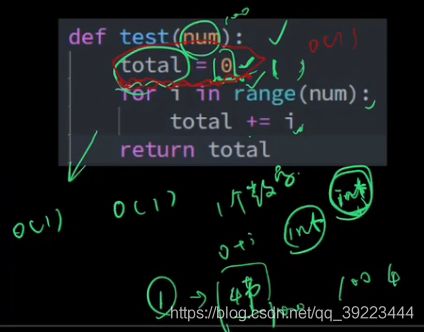
O(1):与num无关

O(n)
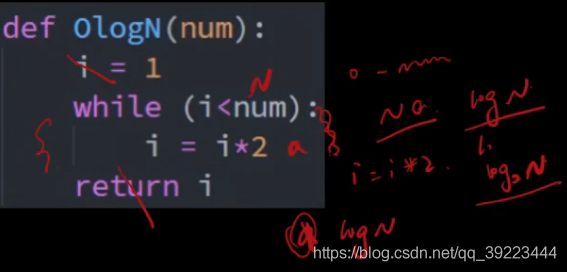
O(log n):2的n次方等于num。典型:二分查找
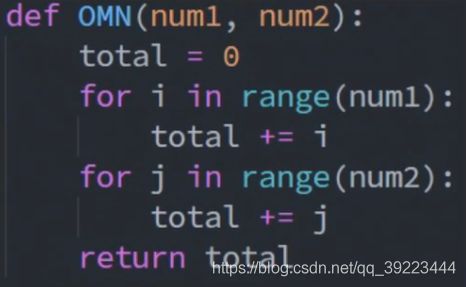
O(m+n):循环并列,相加
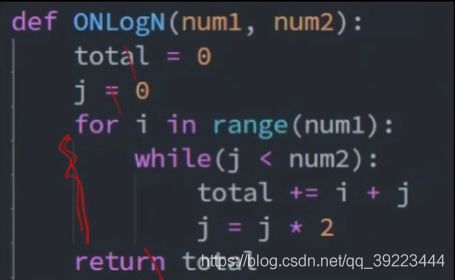
O(nlogn):循环嵌套,相乘。典型:排序

O( n 2 n^2 n2)
2.2 空间复杂度
-
什么是空间复杂度?
算法的存储空间与算法的输入值之间的关系
占空间的都是声明出来的变量
3. 数据结构
线性表
线性表:线性表就是数据排成像一条线一样的结构.每个现行表上的数据最多只有前和后两个方向.常见的线性表结构:数组,链表、队列、栈等。

3.1 数组【Array】
特点: 适合读,不适合写------读多写少
对内存要求高,需要连续的内存空间。
3.1.1 Python常用操作
3.1.2优缺点
3.1.3 练习题
485 最大连续1的个数
int count=0,max=0;
for(int i =0;i<numsSize;i++){
if(nums[i]==1)
count++;
else
count=0;
if(count>max)
max=count;
}
return max;
283 移动零
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
for i in nums:
if i==0:
nums.remove(0)
nums.append(0)
return nums
void moveZeroes(int* nums, int numsSize){
int index=0;
for(int i=0;i<numsSize;i++)
{
if(nums[i] != 0)
{
nums[index] = nums[i];
index++;
}
}
for(int i=index;i<numsSize;i++)
{
nums[i] = 0;
}
}
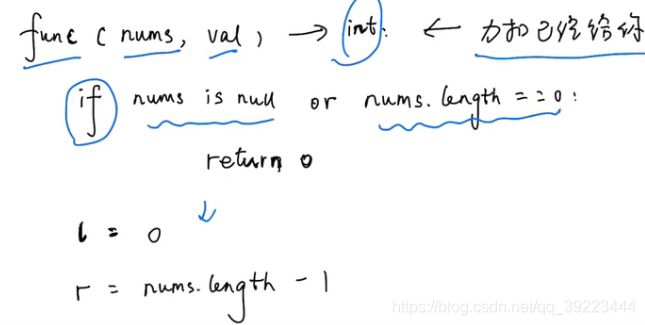
27 移除元素
class Solution:
def removeElement(self, nums, val):
if nums is None or len(nums)==0:
return 0
l,r = 0, len(nums)-1
while l<r:
while(l<r and nums[l] != val):
l=l+1
while(l<r and nums[r] == val):
r=r-1
nums[l],nums[r] = nums[r],nums[l] //将前面不等于val的和后面等于val的交换
return l if nums[l]==val else l+1
class Solution:
def removeElement(self, nums, val):
for i in range(len(nums)-1,-1,-1):
if nums[i] == val:
nums.remove(nums[i])
int removeElement(int* nums, int numsSize, int val){
int index = 0;
for(int i=0;i<numsSize;i++)
{
if(nums[i] != val)
{
nums[index] = nums[i];
index++;
}
}
return index;
}
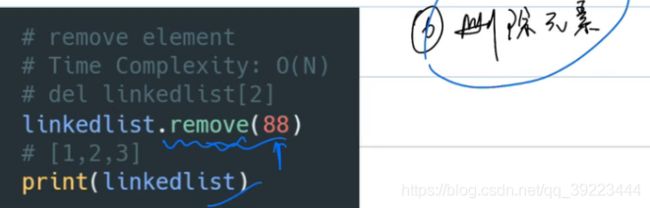
3.2 链表【Linked List】
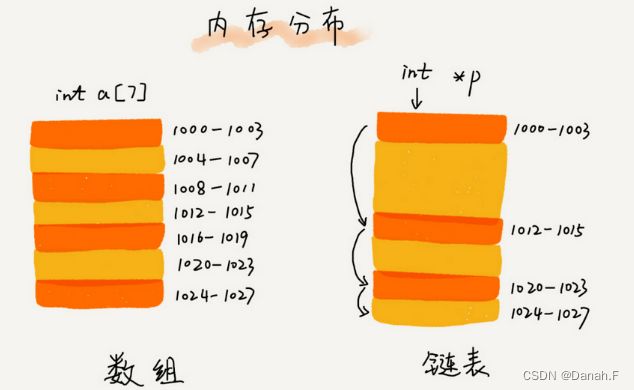
- 从内存结构来看,链表的内存结构是不连续的内存空间,是将一组零散的内存块串联起来,从而进行数据存储的数据结构。
- 链表中的每一个内存块被称为节点Node。节点除了存储数据外,还需记录链上下一个节点的地址,即后继指针next。
- 和数组相比,链表的内存消耗更大,因为每个存储数据的节点都需要额外的空间存储后续指针。
单端链表 √
双端链表 leetcode一般不用
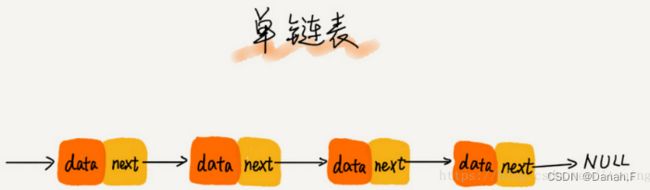
1)每个节点只包含一个指针,即后继指针。
2)单链表有两个特殊的节点,即首节点和尾节点。为什么特殊?用首节点地址表示整条链表,尾节点的后继指针指向空地址null。
3)性能特点:插入和删除节点的时间复杂度为O(1),查找的时间复杂度为O(n)。
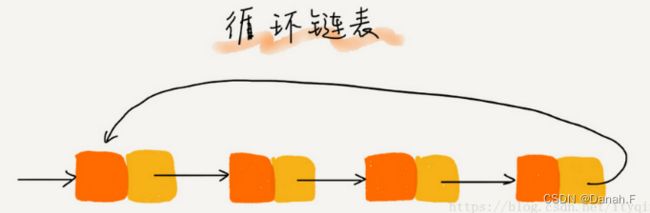
1)除了尾节点的后继指针指向首节点的地址外均与单链表一致。
2)适用于存储有循环特点的数据,比如约瑟夫问题。
双向链表:

1)节点除了存储数据外,还有两个指针分别指向前一个节点地址(前驱指针prev)和下一个节点地址(后继指针next)。
2)首节点的前驱指针prev和尾节点的后继指针均指向空地址。
双向循环链表
特点: 适合写,不适合读------读少写多
3.2.1 Python常用操作
3.2.2 Java常用操作
3.2.3 练习题
203 移除链表元素
class Solution:
def removeElements(self, head: ListNode, val: int) -> ListNode:
dummy = ListNode(0)
dummy.next = head
prev = dummy
while head is not None:
if head.val == val:
prev.next = head.next
head = head.next
else:
prev = head
head = head.next
return dummy.next
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeElements(struct ListNode* head, int val){
struct ListNode*p,*q;
p=head;
while(p!=NULL){
if(p->val==val){
if(p==head){
head=head->next;
}
else{
p=p->next;
q->next=p;
}
}
else{
q=p;
p=p->next;
}
}
return head;
}
//作者:miraitowa
//链接:https://leetcode.cn/problems/remove-linked-list-elements/solutions/2177413/203yi-chu-lian-biao-yuan-su-by-strange-e-upr0/
206 反转链表
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
dummy = ListNode(0)
dummy.next = head
while head is not None and head.next is not None:
dnext = dummy.next
hnext = head.next
dummy.next = hnext
head.next = hnext.next
hnext.next = dnext
return dummy.next
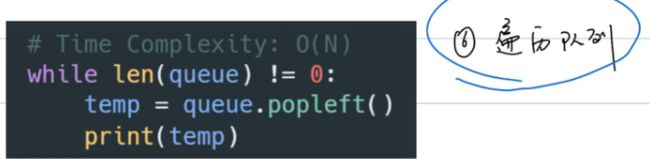
3.3 队列【Queue】
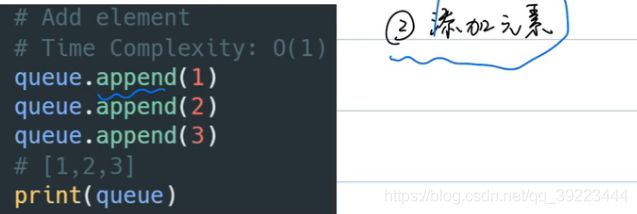
3.3.1 Python常用操作
3.3.2 Java常用操作
3.3.3 练习题
933 最近的请求次数
class RecentCounter:
def __init__(self):
self.q = deque()
def ping(self, t: int) -> int:
self.q.append(t)
while len(self.q)>0 and t-self.q[0]>3000:
self.q.popleft()
return len(self.q)
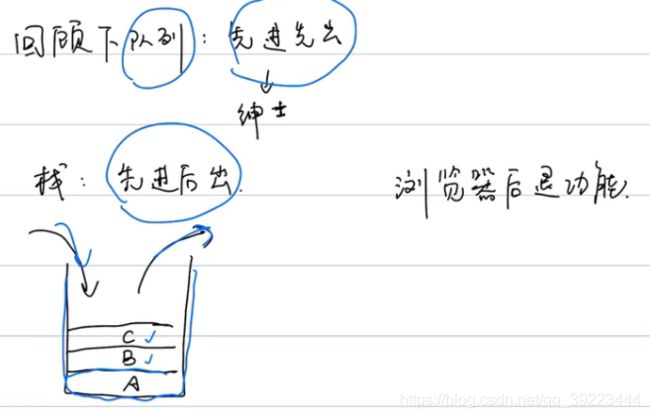
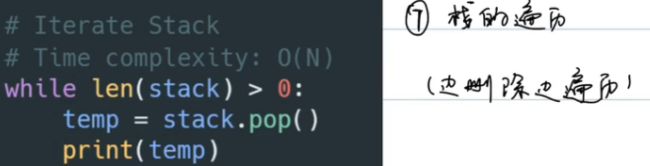
3.4 栈【Stack】
3.4.1 Python常用操作
3.4.2 Java常用操作
3.4.3 练习题
20 有效的括号
class Solution:
def isValid(self, s: str) -> bool:
if len(s)==0:
return True
stack= []
for c in s:
if c == "(" or c == "[" or c == "{":
stack.append(c)
else:
if len(stack) == 0:
return False
else:
temp = stack.pop()
if c == ")":
if temp != "(":
return False
elif c == "]":
if temp != "[":
return False
elif c == "}":
if temp != "{":
return False
return True if len(stack) == 0 else False
bool isValid(char * s){
char a[10000],t;
int i,top=0;
while(s[i] != '\0')
{
if((s[i] == '(')||(s[i] == '[')||(s[i] == '{'))
{
a[top] = s[i];
top++;
}
else
{
if(top>0)
{
top--;
}
else
{
return 0;
}
t = a[top];
if(s[i] == ')')
{
if(t != '(')
{
return 0;
}
}
else if(s[i] == ']')
{
if(t != '[')
{
return 0;
}
}
else if(s[i] == '}')
{
if(t != '{')
{
return 0;
}
}
}
i++;
}
return top==0?1:0;
}
1614 括号的最大嵌套深度
class Solution:
def maxDepth(self, s: str) -> int:
if len(s) == 0:
return 0
stack = []
count = 0
res = 0
for i in s:
# print(i)
if i=="(":
stack.append(i)
count += 1
res = max(res,count)
# print("入栈后:",stack)
# print("res:",res)
else:
if i == ")":
temp = stack.pop()
# print("出站后:",stack)
count -= 1
# print("count:",count)
return res if len(stack) == 0 else 0
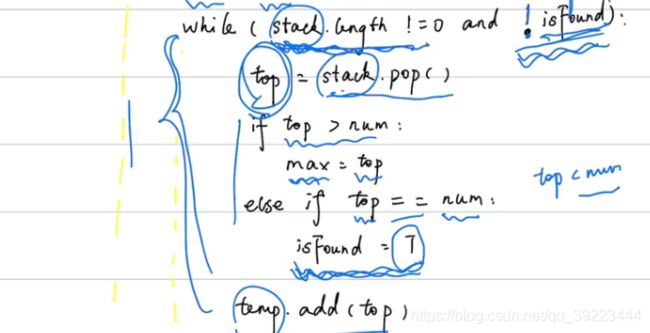
496 下一个更大元素(栈+队列)
class Solution:
def nextGreaterElement(self,nums1: List[int],nums2: List[int]) -> List[int]:
res =[]
stack = []
for num in nums2:
stack.append(num)
for num in nums1:
temp =[]
isFound = False
nextMax = -1
while ( len(stack) != 0 and not isFound ) :
top = stack.pop()
if top > num:
nextMax = top
elif top ==num :
isFound = True
temp.append( top)
res.append( nextMax)
while len(temp) != 0:
stack.append(temp. pop( ))
return res
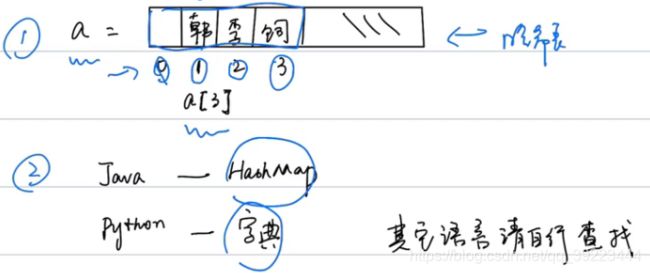
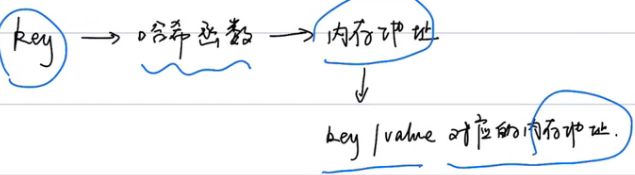
3.5 哈希表【Hash Table】
3.5.1 Python常用操作
3.5.2 Java常用操作
3.5.3 练习题
217 存在重复元素
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
if len(nums) == 0:
return False
dict = {}
for num in nums:
if num not in dict:
dict[num] = 1
else:
dict[num] = dict[num]+1
for v in dict.values():
if v>1:
return True
return False
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
return len(nums) != len(set(nums))
在这里插入代码片
389 找不同
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
if len(s) == 0:
return t
table = [0]*26
for i in range(len(s)):
table[ord(s[i])-ord('a')] -= 1
for j in range(len(t)):
table[ord(t[j])-ord('a')] += 1
for k in range(26):
if table[k] == 1:
ascii = k+ord('a')
return chr(ascii)
496 下一个更大元素
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
stack,hash = [],{}
res = []
for i in nums2:
while len(stack) != 0 and i>stack[-1]:
temp = stack.pop()
hash[temp] = i
stack.append(i)
while len(stack) != 0:
hash[stack.pop()] = -1
for num in nums1:
res.append(hash[num])
return res
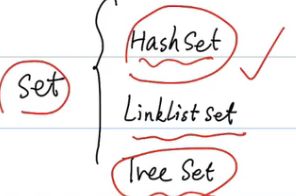
3.6 集合【Set】
无序 不重复
主要作用:
检查某一个元素是否存在
重复元素a


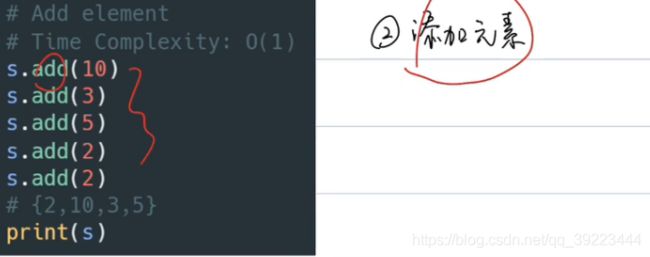
3.6.1 Python常用操作
3.6.2 Java常用操作
3.6.3 练习题
217 存在重复元素
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
set1 = set(nums)
if len(set1) == len(nums):
return False
else:
return True
705 设计哈希集合
class MyHashSet:
def __init__(self):
"""
Initialize your data structure here.
"""
self.hashset = [False]*1000001
def add(self, key: int) -> None:
self.hashset[key]=True
def remove(self, key: int) -> None:
self.hashset[key]=False
def contains(self, key: int) -> bool:
"""
Returns true if this set contains the specified element
"""
return self.hashset[key]
3.7 树【Tree】
![]()
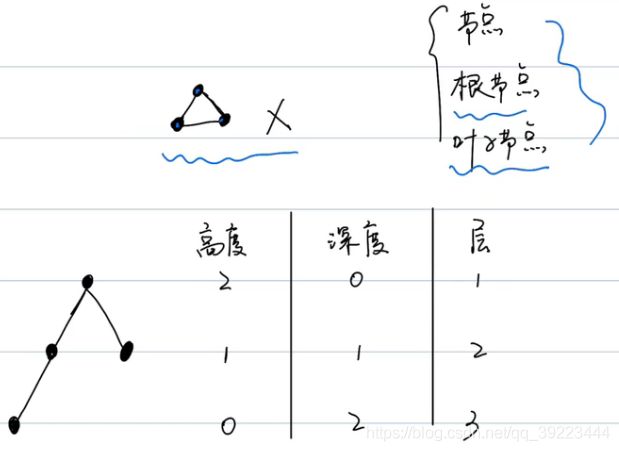
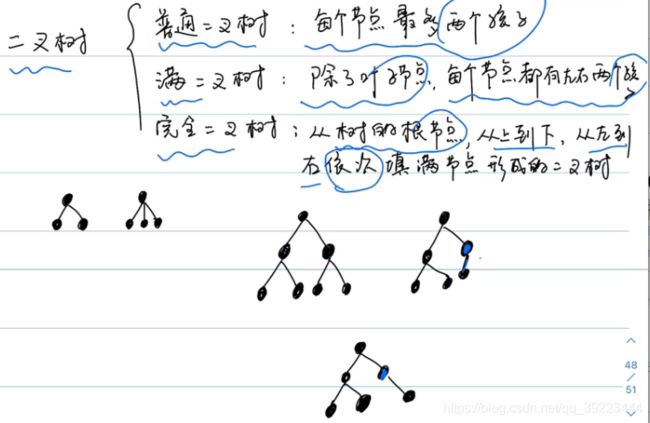
** 满二叉树的所有叶子节点必须在同一层上。**
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。

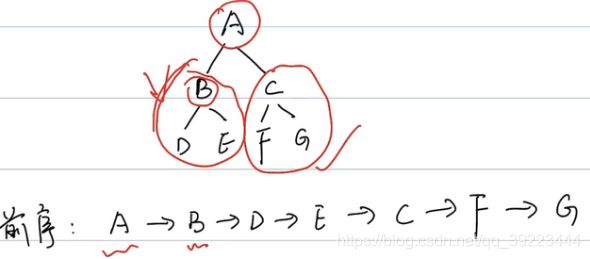
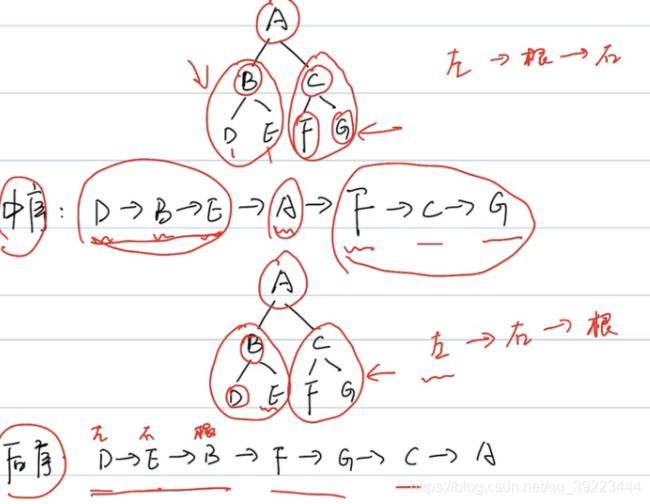
练习题
144
94
145
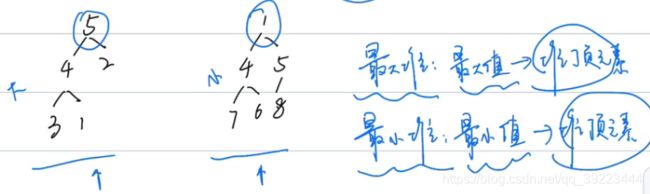
3.8 堆【Heap】
![]()

![]()
![]()
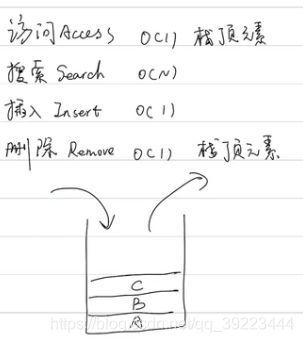
一般删除和搜索都是针对堆顶元素。

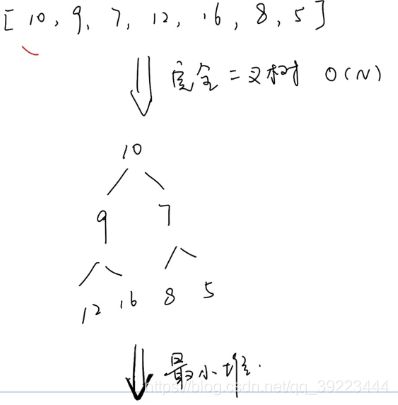
![]()
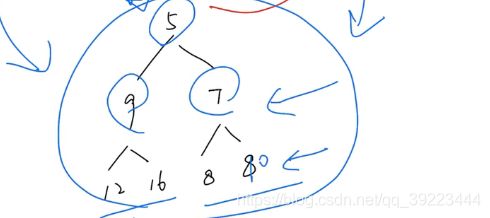
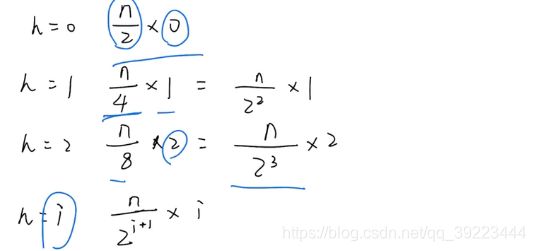
![]()
生成完全二叉树和变成最小堆的过程是并列的,都是O(n),取一个即可。
3.8.1 Python常用操作
3.8.2 Java常用操作
3.8.3 练习题
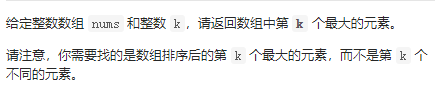
215 数组中第k个最大元素
import heapq
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
heap = []
heapq.heapify(heap)
for num in nums:
heapq.heappush(heap,num*-1)
while k>1:
heapq.heappop(heap)
k=k-1
return heapq.heappop(heap)*-1
可以直接调用函数
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
nums.sort()
return nums[len(nums)-k]
692 前k个高频单词



最大堆的思想是把元素全放在堆中,然后从堆顶一个一个取最大元素

最小堆的的思想是加生成堆的过程中把堆顶的小元素剔除,堆里只剩所需的k个元素,然后再取出。
![]()
只放置k个,加元素的过程中当元素个数大于k时把现有堆的最小值删掉。

![]()

import heapq
class Solution:
def topKFrequent(self, words: List[str], k: int) -> List[str]:
mapping = {}
for word in words:
if word not in mapping:
mapping[word] = 0
mapping[word] = mapping[word] + 1
print(mapping)
heap = []
heapq.heapify(heap)
for key,value in mapping.items():
heapq.heappush(heap,Node(key,value))
if len(heap)>k:
heapq.heappop(heap)
res = []
print(len(heap))
while len(heap)>0:
temp = heapq.heappop(heap)
print(temp.key,":",temp.value)
res.append(temp.key)
res.reverse()
return res
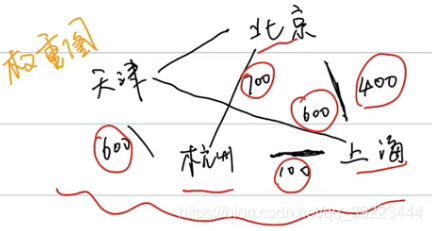
3.9 图【Graph】
3.10 前缀树|字典树【Trie】
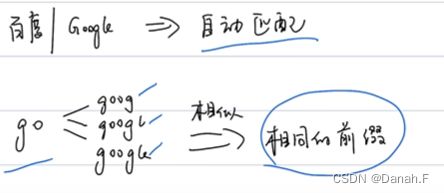
![]()

插入在情况比较好的情况下是O(1),如果内存不够,需要复制到更长的内存空间中区再插入,情况就是O(n)。
N是数组元素的个数,M是匹配的次数。

每次有字母都在节点后面添加,当单词结束时,设置结束flag,这样就标记了有哪些词。

练习题
* 208 Implent Trie 实现Trie[模版]
720
692
3.11 数据结构知识点回顾
4. 算法
4.1 双指针
4.1.1 算法


普通双指针: O(n^2)

对撞双指针: 有序时考虑,O(n)

快慢双指针: 环形链表,快慢指针可相遇
4.1.2 练习题
141 环形链表
class Solution:
def hasCycle(self, head: ListNode) -> bool:
if head is None:
return False
slow = head
fast = head
while fast is not None and fast.next is not None:
fast = fast.next.next
slow = slow.next
if slow == fast:
return True
return False
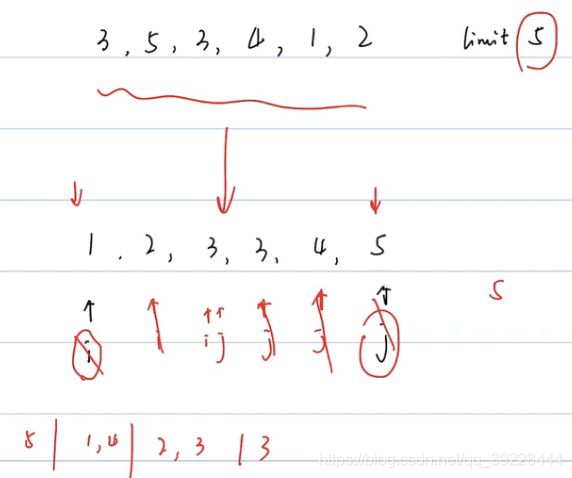
881 救生艇
class Solution:
def numRescueBoats(self, people: List[int], limit: int) -> int:
if people is None or len(people) == 0:
return 0
people.sort()
i=0
j=len(people)-1
res = 0
while(i<=j):
if people[i]+people[j]<= limit:
i = i+1
j=j-1
res = res + 1
return res
4.2 二分查找
4.2.1 算法
4.2.2 练习题
704 二分查找
class Solution:
def search(self, nums: List[int], target: int) -> int:
for i in range(len(nums)):
if nums[i] == target:
return i
return -1
二分法:O(logn)
class Solution:
def search(self, nums: List[int], target: int) -> int:
if nums is None or len(nums) == 0:
return -1
L = 0
R = len(nums) - 1
while L <= R:
mid = L + (R - L ) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
R = mid-1
else:
L = mid+1
return -1
35 搜索插入位置
if nums ==None or len( nums) == 0:
return 0
prev = -1
for i in range( len( nums )):
if nums[i] == target:
return i
elif nums[i] < target:
prev = i
else:
return prev+1
return prev+1
二分法
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
if nums ==None or len( nums) == 0:
return 0
left = 0
right = len(nums)
while( left < right):
mid = left + ( right - left)//2
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid
else:
left = mid + 1
return left
自己的解法(菜狗的解法)
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
L = 0
R = len(nums) - 1
while L <= R:
mid = L + (R - L ) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target :
if mid-1 < 0 or nums[mid - 1] < target:
return mid
else:
R = mid-1
else:
if mid+1 == len(nums) or nums[mid + 1] > target:
print(mid+1)
return mid+1
else:
L = mid+1
int searchInsert(int* nums, int numsSize, int target){
int low = 0;
int high = numsSize-1;
while(low<high)
{
int mid = low+(high-low)/2;
if(nums[mid]==target)
return mid;
else if(nums[mid]>target)
high = mid;
else
low = mid+1;
}
if(nums[low] >= target)
return low;
else
return low+1;
}
162 寻找峰值
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
if nums is None or len(nums) == 0:
return
left = 0
right = len(nums)-1
while left < right:
mid = left+(right-left)//2
if nums[mid] > nums[mid+1]:
right = mid
else:
left = mid + 1
return left
74 搜索二维矩阵
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if matrix == None or len(matrix)==0:
return False
row = len(matrix)
col = len(matrix[0])
low = 0
high = row*col-1
while(low<=high):
mid = low+(high-low)//2
element = matrix[mid//col][mid%col]
if element == target:
return True
elif element > target:
high = mid-1
else:
low = mid+1
return False
bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
if(matrix == NULL)
return 0;
int row = matrixSize;
int col = matrixColSize[0];
int low = 0;
int high = row*col-1;
while(low<=high)
{
int mid = low+(high-low)/2;
int element = matrix[mid/col][mid%col];
if(element == target)
return 1;
else if(element > target)
high = mid-1;
else
low = mid+1;
}
return 0;
}
4.3 滑动窗口(技巧)
目的:减少while循环
数组中的定长问题。
4.3.1 算法
一开始窗口的左边界和右边界都停留在数组的最左侧,窗口是空的,窗口的左边界和右边界只能向右移动,同时左边界不能超过右边界的右边(L不能超过R)。
当R往右移动时,表示数组中有若干个元素从窗口的右侧进窗口。
当L往左移动时,表示数组中有若干个元素从窗口的左侧出窗口。
4.3.2 练习题
209 长度最小的子数组
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
if nums is None or len(nums) == 0:
return 0
res = len(nums)+1
i=0
j=0
total = 0
while j<len(nums):
total = total+nums[j] /窗口向右移,
j = j+1
while total >= target:
res = min(res,j-i)
total = total - nums[i]/如果值满足要求,窗向左移
i = i+1
if res == len(nums)+1:
return 0
else:
return res
int minSubArrayLen(int s, int *nums, int numsSize) {
if (numsSize == 0) {
return 0;
}
int ans = INT_MAX;
int start = 0, end = 0;
int sum = 0;
while (end < numsSize) {
sum += nums[end];
while (sum >= s) {
ans = fmin(ans, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}
return ans == INT_MAX ? 0 : ans;
}
int minSubArrayLen(int target, int* nums, int numsSize){
if(numsSize==0)
return 0;
int i,j=0;
int sum = 0;
int result = numsSize+1;
while(j<numsSize)
{
sum = sum+nums[j];
j++;
while(sum>=target)
{
result = fmin(result,j-i);
sum = sum-nums[i];
i++;
}
}
if(result == numsSize+1)
return 0;
else
return result;
}//内存错误,暂未找到原因
链接:力扣官网
1456 定长子串中元音的最大数组
class Solution:
def maxVowels(self, s: str, k: int) -> int:
if s is None or len(s) == 0 or len(s)<k:
return 0
hashset = set(['a','e','i','o','u'])
count = 0
res = 0
for i in range(0,k):
if s[i] in hashset:
count = count+1
res = max(res,count)
for i in range(k,len(s)):
out = s[i-k]
inc = s[i]
if out in hashset:
count = count - 1
if inc in hashset:
count = count + 1
res = max(res,count)
return res
int maxVowels(char * s, int k){
int len = strlen(s);
/* 搞个数组来存,1表示元音,0表示辅音 */
int *array = (int*)calloc(len, sizeof(int));
for (int i = 0; i < len; i++) {
if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u') {
array[i] = 1;
}
}
/* 计算第一个窗口 */
int sum = 0;
for (int i = 0; i < k; i++) {
sum += array[i];
}
/* 滑动窗口 */
int ans = sum;
for (int i = k; i < len; i++) {
sum = sum - array[i - k] + array[i];
ans = fmax(ans, sum);
}
return ans;
}
4.4 递归 recursion
4.4.1 算法


递归是一种非常高效、简洁的编码技巧,一种应用非常广泛的算法,比如DFS深度优先搜索、前中后序二叉树遍历等都是使用递归。
什么样的问题可以用递归解决呢?
一个问题只要同时满足以下3个条件,就可以用递归来解决:
1.问题的解可以分解为几个子问题的解。何为子问题?就是数据规模更小的问题。
2.问题与子问题,除了数据规模不同,求解思路完全一样
3.存在递归终止条件
如何实现递归
- 递归代码编写
写递归代码的关键就是找到如何将大问题分解为小问题的规律,并且基于此写出递推公式,然后再推敲终止条件,最后将递推公式和终止条件翻译成代码。 - 递归代码理解
对于递归代码,若试图想清楚整个递和归的过程,实际上是进入了一个思维误区。
那该如何理解递归代码呢?如果一个问题A可以分解为若干个子问题B、C、D,你可以假设子问题B、C、D已经解决。而且,你只需要思考问题A与子问题B、C、D两层之间的关系即可,不需要一层层往下思考子问题与子子问题,子子问题与子子子问题之间的关系。屏蔽掉递归细节,这样子理解起来就简单多了。
因此,理解递归代码,就把它抽象成一个递推公式,不用想一层层的调用关系,不要试图用人脑去分解递归的每个步骤。
递归常见问题:
1.警惕堆栈溢出:可以声明一个全局变量来控制递归的深度,从而避免堆栈溢出。
2.警惕重复计算:通过某种数据结构来保存已经求解过的值,从而避免重复计算。




时间复杂度:O(n^20)
空间复杂度:O(n)
4.4.2 练习题
509 斐波那契数列
![]()
class Solution:
def fib(self, n: int) -> int:
if n < 2:
return 1 if n==1 else 0
sum = self.fib(n-1) + self.fib(n-2)
return sum
int fib(int n){
if(n<2)
return n;
else
return fib(n-1)+fib(n-2);
}
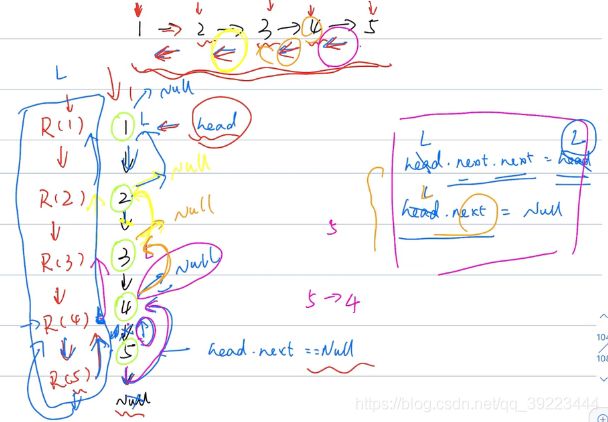
206 反转链表
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
if head is None or head.next is None:
return head
p = self.reverseList(head.next)
head.next.next = head
head.next = None
return p
344 反转字符串
class Solution:
def reverseString(self, s: List[str]) -> None:
self.recursion(s,0,len(s)-1)
def recursion(self,s,left,right):
if left>=right:
return
self.recursion(s,left+1,right-1)
s[left],s[right] = s[right],s[left]
# 双指针
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
l = 0
r = len(s)-1
while l < r:
s[l],s[r] = s[r],s[l]
l += 1
r -= 1
return s
void reverseString(char* s, int sSize){
reversion(s, 0, sSize-1);
}
void reversion(char *s,int left,int right)
{
if(left>=right)
return;
char temp = s[left];
s[left] = s[right];
s[right] = temp;
reversion(s,left+1,right-1);
}
void reverseString(char* s, int sSize){
for(int left=0,right=sSize-1;left<right;++left,--right)
{
char temp = s[left];
s[left] = s[right];
s[right] = temp;
}
}
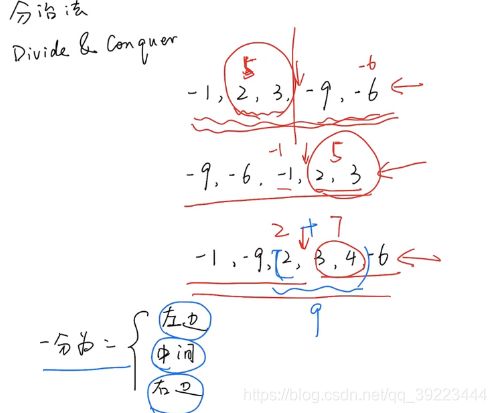
4.5 分治法(divide & conquer)
4.5.1 算法
4.5.2 练习题
169 多数元素
# 排序法
class Solution:
def majorityElement(self, nums: List[int]) -> int:
nums.sort()
half = len(nums)//2
return nums[half]
# 哈希表
class Solution:
def majorityElement(self, nums: List[int]) -> int:
hashset = {}
for i in nums:
if i not in hashset:
hashset[i] = 0
hashset[i] = hashset[i] + 1
half = len(nums)//2
for key in hashset.keys():
if hashset[key] > half:
return key
return -1
class Solution:
def majorityElement(self, nums: List[int]) -> int:
return self.majority(nums,0,len(nums)-1)
def majority(self,nums,l,r):
if l==r:
return nums[l]
mid = l + (r-l)//2
leftmajority = self.majority(nums,l,mid)
rightmajority = self.majority(nums,mid+1,r)
if leftmajority==rightmajority:
return leftmajority
else:
leftcount = 0
rightcount = 0
for i in nums[l:r+1]:
if i == leftmajority:
leftcount = leftcount+1
if i == rightmajority:
rightcount = rightcount+1
return leftmajority if leftcount > rightcount else rightmajority
53 最大子序列
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
# 暴力法1,超时
# count = 1
# max1 = float('-inf')
# while count<=len(nums):
# for i in range(0,len(nums)-count+1):
# sum1 = sum(nums[i:i+count])
# max1 = max(max1,sum1)
# count += 1
# return max1
# 暴力法2,超时
result = float('-inf')
for i in range(0,len(nums)):
temp = 0
for j in range(i,len(nums)):
temp = temp+nums[j]
result = max(result,temp)
return result
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
for i in range(1, len(nums)):
nums[i]= nums[i] + max(nums[i-1], 0)
return max(nums)
4.6 回溯法(Backtracking)
4.6.1 算法
4.6.2 练习题
22 括号生成
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
result = []
self.backtracking(n, result, 0, 0, "")
return result
def backtracking(self,n, result, left, right, str):
if right > left:
return
if right == left == n:
result.append(str)
return
if left<n:
self.backtracking(n, result, left+1,right, str+"(")
if right<left:
self.backtracking(n, result, left, right+1, str+")")
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
#define MAX_SIZE 1430
char ** generateParenthesis(int n, int* returnSize){
char *str = (char*)calloc((2 * n + 1), sizeof(char));
char **result = (char **)malloc(sizeof(char *) * MAX_SIZE);
*returnSize=0;
generate(0, 0, n, str, 0, result, returnSize);
return result;
}
void generate(int left, int right, int n, char *str, int index, char **result, int *returnSize)
{
if(index == 2 * n)
{
result[(*returnSize)] = (char*)calloc((2*n+1),sizeof(char));
strcpy(result[(*returnSize)++],str);
}
if(left<n)
{
str[index] = '(';
generate(left + 1, right, n, str, index + 1, result, returnSize);
}
if(right<left)
{
str[index] = ')';
generate(left, right+1, n, str, index + 1, result, returnSize);
}
}
78 子集
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
for i in range(0,len(nums)+1):
self.backtracking(i, result, 0, nums, [])
return result
def backtracking(self, length, result, index, nums, subset):
if len(subset) == length:
result.append(subset[:])
return
# print(result)
for i in range(index,len(nums)):
subset.append(nums[i])
self.backtracking(length, result, i+1, nums, subset)
subset.pop()
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = [[]]
for num in nums:
temp=[]
for cur in result:
temp.append(cur+[num])
for t in temp:
result.append(t)
return result
![]()
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result=[]
self.dfs(nums,result,0,[])
return result
def dfs(self,nums,result,index,subset):
result.append(subset[:])
if index == len(nums):
return
for i in range(index,len(nums)):
subset.append(nums[i])
self.dfs(nums,result,i+1,subset)
subset.pop()
77 组合
# 使用python库
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
return list(itertools.combinations(range(1, n+1), k))
# dfs
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
self.dfs(n, k, 1, result, [])
return result
def dfs(self,n,k,index,result,subset):
if len(subset) == k:
result.append(subset[:])
return
for i in range(index,n+1):
subset.append(i)
self.dfs(n,k,i+1,result,subset)
subset.pop()
46 全排列
华为OD 组装新的数组
import sys
arr = list(map(int,input().split()))
num = int(input())
def dfs(newArr,index,sum_arr,minV,num,count):
if sum_arr> num:
return count
if sum_arr == num or (0 < sum_arr-num < minV):
return count+1
for i in range(index,len(arr)):
count = dfs(newArr,i,sum+newArr[i],minV,count)#对每个元素进行递归调用,计算和并计数
def getResult(arr,num):
newArr = []
for i in arr:
if i<=num:
newArr.append(i)
minVal = min(newArr)
return dfs(newArr,0,0,minVal,num,0)
51 N皇后
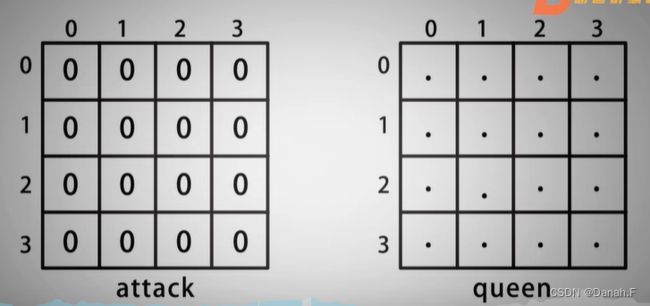
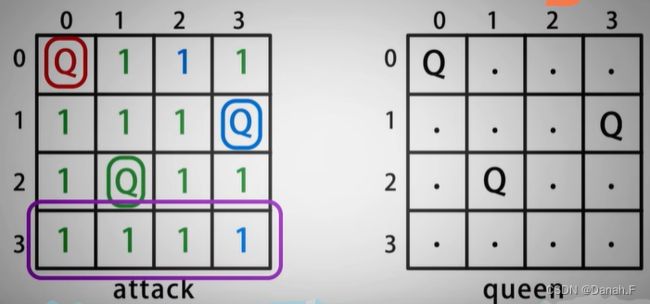
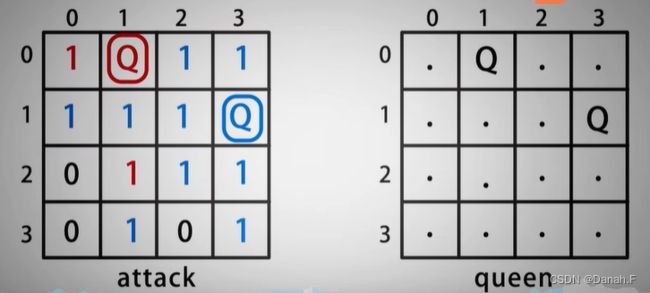
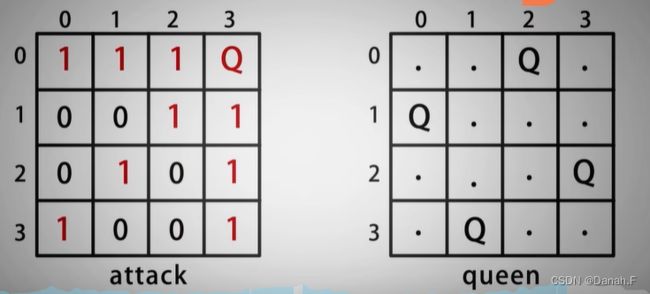
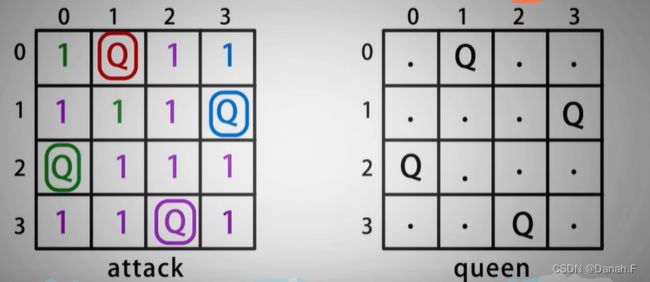
 我们需要标记棋盘的两种状态,棋盘是否可放置皇后以及棋盘放置皇后的位置,使用数组attack[][]表示棋盘是否可放置皇后,初始化所有元素为0,0表示可以放,1表示不可以放;使用二维数组queen[][]表示皇后的位置,初始化所有元素为
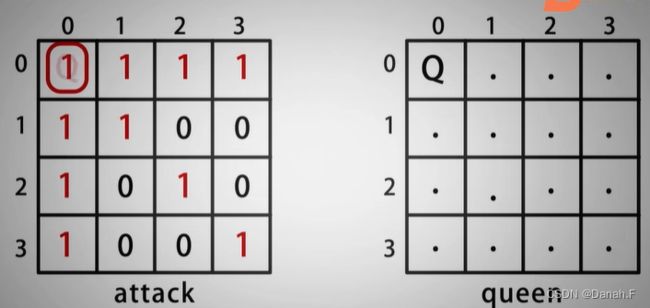
我们需要标记棋盘的两种状态,棋盘是否可放置皇后以及棋盘放置皇后的位置,使用数组attack[][]表示棋盘是否可放置皇后,初始化所有元素为0,0表示可以放,1表示不可以放;使用二维数组queen[][]表示皇后的位置,初始化所有元素为., .表示没有放置皇后,Q表示放置了皇后。
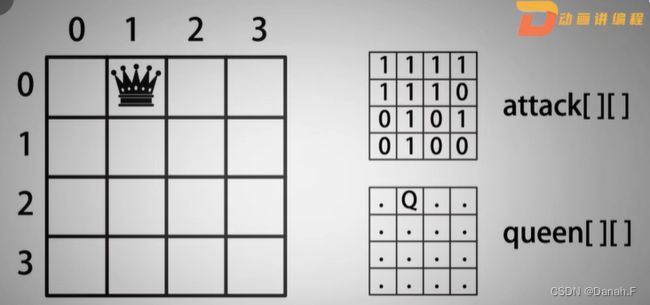
在[0][0]位置放置皇后后,将attack[][]中相应的8个方向的0修改为1,同时将queen中第0行第0列改为Q,这样就实现了标记棋盘是否可放置皇后与皇后位置存储。
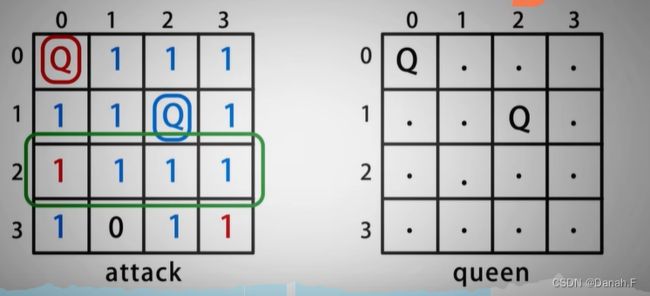
然后看皇后可攻击范围的表示方法,皇后可以攻击上下左右、左上、左下、右上、右下,表示方法如下图:

![]()
在attack数组中,将防止皇后位置的8个方向分别延伸到n,延伸过程中不可超过数组边界,放置皇后和标记棋盘算法设计如下:
//自定义函数put_queen,实现在(x, y)放置皇后,对attack数组的更新
//x、 y表示放置皇后的坐标,二维数组attack表示棋盘是否可放置皇后
void put_queen(int x, int y, vector<vector<int>> &attack){
//定义常量方向数组,方便后面对8个方向进行标记
static const int dx[]={-1, 1,0,0,-1,-1,1,1};
static const int dy[]={0, 0,-1,1,-1,1,-1,1};
attack[x][y] =1;//将皇后位置标记为1
//通过两层循环,将该皇后可能攻击到的位置进行标记,
for (int i= 1; i<attack.size(); i++){//外层循环表示从皇后位置向1到n-1个距离延伸
for (int j = 0; j<8; j++){//内层遍历8个方向,生成新的位置
int nx =x+i *dx[j];//生成新的位置行
int ny =y+i *dy[j];//生成新的位置列
if(nx>=0 && nx<attack.size() && ny>=0 && ny<attack.size())
{
attak[nx][ny] == 1;
}
}
}
}
- 如果将皇后放在第0行第0列,按照8个方向更新数组,并将queen[0][0]标记为Q,算法整体递归地对棋盘每一行放皇后,遍历可以放皇后的列,找到可以放皇后的列后放置皇后,更新attack数组,并递归下一行的皇后放置,
- 如果没有位置可以放置,说明上一行放错了, 则需要恢复上一个attack和queen数组,重新选择上一行的皇后位置,将皇后放在下一个可以放置的位置,这就是回溯的思想。
- 如果上一行的所有列都经过尝试,后面依旧没有合适的位置放皇后,则说明第0行的皇后位置是错的,回溯到第0行重新选择,
- 当完成第n个皇后的放置后,将结果保存,然后回溯到当前行未放皇后的状态,重新尝试下一个可能的列,
- 如果全部可能的列都经过尝试,就再继续向前回溯,直到第0行所有的列都被尝试。
//回湖法求解N皇后的递归函数
//k表示当前处理的行
//n表示N皇后问题
//queen存储皇后的位置
//attack标记皇后的攻击位置
//solve存储N皇后的全部解法
void backtrack(int k,int n, vector<string> &queen, vector<vector<int>>&attack, vector<vector<string>>&solve){
if (k == n){//找到一组解
solve.push_back(queen);//将结果queen保存到solve
return;
}
//遍历0至n-1列,在循环中,回溯试探皇后可知放置的位置
for (inti= 0;i<n; i++){
if(attack[k][i] == 0)//判断当前第k行第i列是否可以放置皇后
vector<vector<int> > tmp = attack;//备份attack数组
queen[k][i] ='Q';1/标记该位置为'Q'
put_queen(k,i, attack);//更新attack数组
backtrack(k+1, n, queen, attack, solve);//递归试探k+1行的皇后放置
attack_=tmp;//恢复attack数组
queen[k][i]='.';//恢复queen数组
}
}
}
vector<vector<string> >solveNQueens(int n){
vector<vector<string> >solve;//存储最后结果
vector<vector<int> >attack;//标记皇后的攻击位置
vector<string> queep;//保存皇后位置
//使用循环初始化at
for (int i= 0;i<n;i++){
attack.push_back((std::vector<int>()));
for (int j = o; j<n; j++){
attack[i].push_back(O);
}
queen.push_back("");
queen[i].append(n,'.');
}
backtrack(0, n, queen, attack, solve);//调用backtrack求解N皇后问题
return solve;
}
int main(){
vector<vector<string>>result;
result = solveNQueens(8);
//打印出8皇后的解法
printf("8皇后共有%d种解法:\n\n ",result.size())for (int i = 0; i<result.size(); i++){
printf("解法%d:\n", i+1);
for (int j = 0; j < result[i].size(); j++){
printf("%s\n", result[i][j].c_str());
}
printf("\n");
}
return 0;
}
36 有效的数独
# 条件判断
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
for i in range(9):
list1 = []
for j in range(9):
if board[i][j] not in list1 and board[i][j] != ".":
list1.append(board[i][j])
elif board[i][j] in list1:
return False
for j in range(9):
list2 = []
for i in range(9):
if board[i][j] not in list2 and board[i][j] != ".":
list2.append(board[i][j])
elif board[i][j] in list2:
return False
for n1 in [0,3,6]:
for n2 in [0,3,6]:
list3 = []
for i in range(n1,n1+3):
for j in range(n2,n2+3):
if board[i][j] not in list3 and board[i][j] != ".":
list3.append(board[i][j])
elif board[i][j] in list3:
return False
return True
# 哈希
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
row = [[0] * 9 for _ in range(9)]#标记1-9的所有值是否被使用,如果已经被使用,返回错误,否则标记为已使用
col = [[0] * 9 for _ in range(9)]
block = [[0] * 9 for _ in range(9)]
for i in range(9):
for j in range(9):
if board[i][j] != '.':
num = int(board[i][j]) - 1
b = (i // 3) * 3 + j // 3
if row[i][num] or col[j][num] or block[b][num]:
return False
row[i][num] = col[j][num] = block[b][num] = 1
return True
作者:liupengsay
链接:https://leetcode.cn/problems/valid-sudoku/solutions/1766666/er-xu-cheng-ming-jiu-xu-zui-python3ha-xi-szko/
来源:力扣(LeetCode)
4.7 深度优先搜索(DFS)
4.7.1 算法
深度优先搜索是先设置终止条件,然后再范围内进行dfs的循环;广度有限搜索需要借助队列,先判断条件,在满足条件时存入队列,不满足条件时退出,返回结果。
4.7.2 练习题
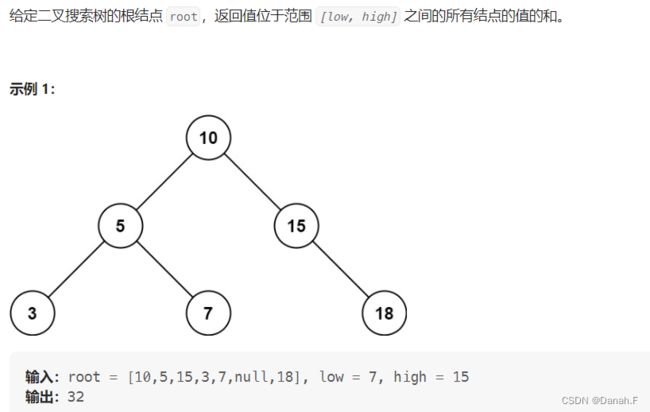
938 二叉搜索树的范围和
按深度优先搜索的顺序计算范围和。记当前子树根节点为 root\textit{root}root,分以下四种情况讨论:
-
root节点为空,返回0.
-
root节点的值大于 high
由于二叉搜索树右子树上所有节点的值均大于根节点的值,即均大于 high,故无需考虑右子树,返回左子树的范围和。 -
root节点的值小于 low
由于二叉搜索树左子树上所有节点的值均小于根节点的值,即均小于low,故无需考虑左子树,返回右子树的范围和。 -
root节点的值在 [low,high] 范围内
此时应返回 root节点的值、左子树的范围和、右子树的范围和这三者之和。
# dfs
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
if not root:
return 0
if root.val>high:
return self.rangeSumBST(root.left,low,high)
if root.val<low:
return self.rangeSumBST(root.right,low,high)
return root.val+self.rangeSumBST(root.left,low,high)+self.rangeSumBST(root.right,low,high)
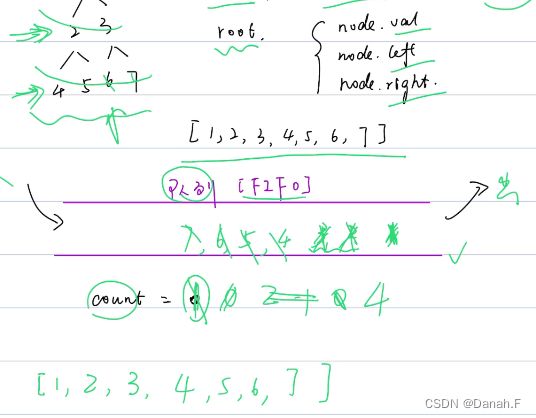
# bfs
class Solution:
def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
total = 0
q = collections.deque([root])
print("q:",q)
while q:
node = q.popleft()
if not node:
continue
if node.val > high:
q.append(node.left)
elif node.val < low:
q.append(node.right)
else:
total += node.val
q.append(node.left)
q.append(node.right)
return total
#bfs另一种写法,把值一层一层放进队列中,然后进行判断计算
class Solution:
def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
total = 0
q = []
q.append(root)
while q:
node = q.pop(0)
if node.val >= low and node.val <= high:
total += node.val
if node.left != None:
q.append(node.left)
if node.right != None:
q.append(node.right)
return total
78 子集
见回溯法。
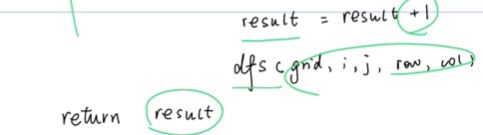
200 岛屿数量
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if grid is None or len(grid) == 0:
return 0
result = 0
row = len(grid)
col = len(grid[0])
for i in range(0,row):
for j in range(0,col):
if grid[i][j] == '1':
result += 1
self.dfs(grid,i,j,row,col)
return result
def dfs(self,grid,x,y,row,col):
if x<0 or y<0 or x>= row or y>= col or grid[x][y] == '0':
return
grid[x][y] = '0'
self.dfs(grid,x-1,y,row,col)
self.dfs(grid,x+1,y,row,col)
self.dfs(grid,x,y-1,row,col)
self.dfs(grid,x,y+1,row,col)
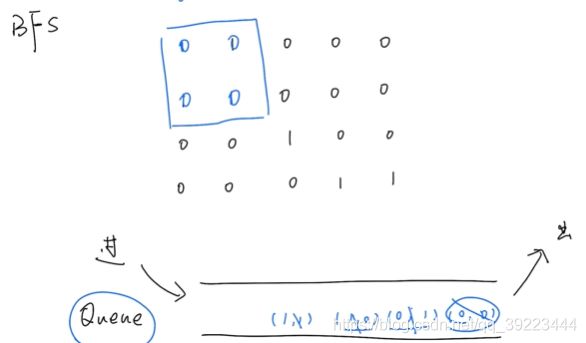
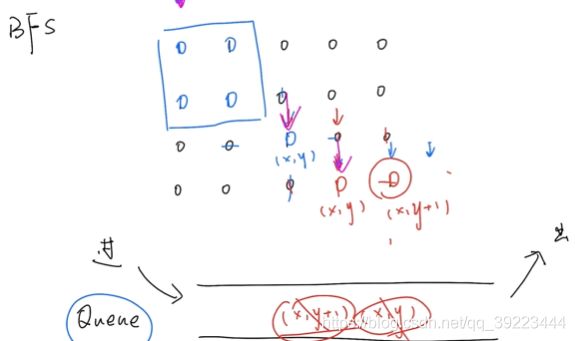
BFS:
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if grid is None or len(grid) == 0:
return 0
result = 0
row = len(grid)
col = len(grid[0])
q = []
for i in range(0,row):
for j in range(0,col):
if grid[i][j] == '1':
result += 1
q.append([i,j])
grid[i][j] == '0'
while len(q)>0:
cur = q.pop()
x = cur[0]
y = cur[1]
if x-1 >= 0 and grid[x-1][y] == '1':
q.append([x-1,y])
grid[x-1][y] == '0'
if y-1 >= 0 and grid[x][y-1] == '1':
q.append([x,y-1])
grid[x][y-1] == '0'
if x+1 < row and grid[x+1][y] == '1':
q.append([x+1,y])
grid[x+1][y] == '0'
if y+1 < col and grid[x][y+1] == '1':
q.append([x,y+1])
grid[x][y+1] == '0'
return result
4.8 广度优先搜索(BFS)
4.8.1 算法
每次把根节点存到列表中;判断节点是否有孩子,如果有,则将节点从列表中pop()出来,然后将孩子放进列表中,如果没有,则直接pop出去。
4.8.2 练习题
938 二叉搜索树的范围和
102 二叉树的层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
res = []
q = []
q.append(root)
while q:
n = len(q)
temp = []
for i in range(n):
node = q.pop(0)
# print(node)
temp.append(node.val)
print(temp)
if node.left != None:
q.append(node.left)
if node.right != None:
q.append(node.right)
res.append(temp)
return res
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
res = []
q = []
q.append(root)
while q:
temp = q
level = []
q = []
for node in temp:
level.append(node.val)
if node.left != None:
q.append(node.left)
if node.right != None:
q.append(node.right)
res.append(level)
return res
107 二叉树的层序遍历II
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
res = []
q = []
q.append(root)
while q:
n = len(q)
temp = []
for i in range(n):
node = q.pop(0)
# print(node)
temp.append(node.val)
print(temp)
if node.left != None:
q.append(node.left)
if node.right != None:
q.append(node.right)
res.append(temp)
return res[::-1]
117 填充每个节点的下一个右侧节点指针II
class Solution:
def connect(self, root: 'Node') -> 'Node':
if root is None:
return root
res = []
q = []
q.append(root)
while q:
temp = q
q = []
for x,y in pairwise(temp):
x.next = y
for node in temp:
if node.left != None:
q.append(node.left)
if node.right != None:
q.append(node.right)
return root
655 输出二叉树
662 二叉树最大宽度
4.9 动态规划
4.9.1 算法
- 明确dp(i)表示什么
- 根据dp(i)和dp(i-1)的关系得到状态转移方程
- 确定初始条件,如dp(0)
- 终止状态
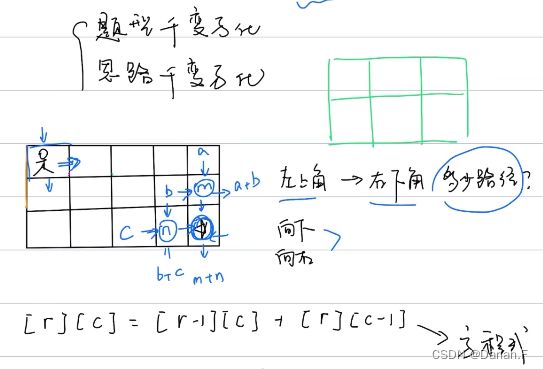
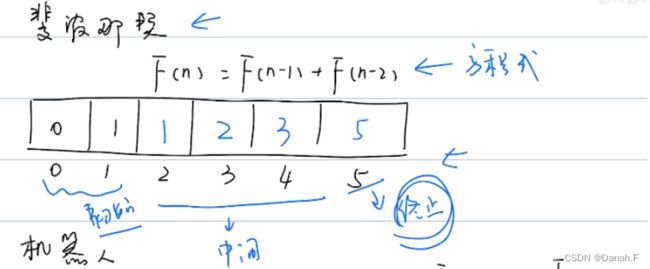
斐波那契数列是一维数组,机器人则是二维数组,将起点到终点之间所有的值存储到二维数组中。
一个小人从左上角到达右下角有很多条路径,每个格子之前的点只能是上面或者前面,也就是要得到某个方格的路径,必须知道它前面或者上面的路径,到达它的路径数等于两个方向的路径之和。

4.9.2 练习题
509 斐波那契数列
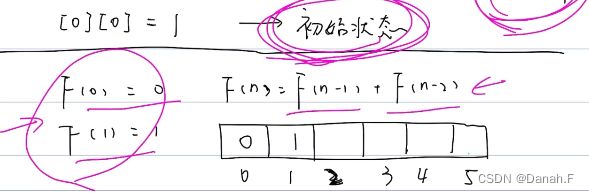
初始状态:f(0)=0,f(1)=1
状态转移方程:f(n)=f(n-1)+f(n-2)
终止条件:f(0)=0,f(1)=1
# python
class Solution:
def fib(self, n: int) -> int:
if n < 2:
return n
p, q, r = 0, 0, 1
for i in range(2, n + 1):
p, q = q, r
r = p + q
return r
//C
int fib(int n)
{
if(n<2)
return n;
int p=0,q=0,r=1;
for(int i=0;i<=n;i++)
{
p = q;
q = r;
r =p + q;
}
return r
}
62 不同路径

初始条件,位于[0,0]位置
状态方程:f(m,n)=f(m-1,n)+f(m,n-1)
结束条件:达到[m,n]
#python
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[1]*n] + [[1]+[0]*(n-1) for _ in range(m-1)]
# print(dp)
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i-1][j]+dp[i][j-1]
return dp[-1][-1]
#python优化算法,复杂度为2*n?
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
pre = [1]*n
cur = [1]*n
# print(dp)
for i in range(1,m):
for j in range(1,n):
cur[j] = cur[j-1]+pre[j]
pre = cur[:]
return pre[-1]
//C
int uniquePaths(int m, int n){
int dp[m][n];
for(int i=0;i<m;i++)
{
dp[i][0] = 1;
}
for(int i=0;i<n;i++)
{
dp[0][i] = 1;
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
121 买卖股票的最佳时机

买股票的最佳时机有很多种,还包括含冷冻期、手续费等,本题属于入门题目。
股票问题的方法就是动态规划,因为它包含了重叠子问题,即买卖股票的最佳时机是由之前买或者不买的状态决定的,而之前买或者不买又是由更早的状态决定的。
由于本题只有一笔交易(买入卖出),因此除了动态规划还有更加简单的方法:一次遍历,遍历一遍数组。计算每次到当天为止的最小股票价格和最大利润。
# python 一次遍历
class Solution:
def maxProfit(self, prices: List[int]) -> int:
minPrices = inf
maxProfit = 0
for i in prices:
minPrices = min(i, minPrices)
maxProfit = max(i-minPrices, maxProfit)
return maxProfit
# python 动态规划
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n==0:
return 0
dp = [0]*n
minPrices = prices[0]
for i in range(1,n):
minPrices = min(prices[i], minPrices)
dp[i] = max(prices[i]-minPrices, dp[i-1])
return dp[-1]
以下股票问题都来自于leetcode这篇文章:一个方法团灭 6 道股票问题
- dp代表什么,状态转移方程怎么写
dp表示利润。
利用【状态】穷举,具体到每一天,看看总共有几种可能的状态,再找出每个状态对应的选择,穷举所有状态,针对每个状态的不同选择更新状态。
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2,...)
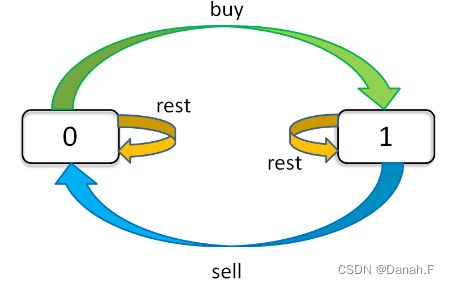
比如股票问题,每天有三种选择:买入、卖出、无操作,用buy、sell、reset表示,而且这三种选择是有条件的,因为sell必须在buy之后,buy必须在sell之后,reset可以在buy之后reset或者sell之后 reset。另外如果有交易次数的限制,buy只能在k>0的情况下进行。
看穷举的状态很复杂,那么我们怎么列举出来呢。这个问题的【状态】有三个,第一个是天数,第二个是允许交易的最大次数,第三个是当前状态(这时我们可以将买入、卖出当成动作,在不同的动作下,当前状态会改变),我们可以用三维数组表示全部的组合。
dp[i][k][0 or 1]
0<=i<=n-1,1<=k<=K
n为天数,K为最多交易数,0表示没有持有,1是持有
这个问题现在有n*K*2种状态,全部穷举就可以搞定
for 0<=idp[3][2][1]的含义是:今天是第三天,现在手上持有股票,从现在开始最多进行2次交易。
我们想求得最终答案是dp[n-1][K][0],即最后一天,最多允许K次交易,最多获得多少利润。
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])
max(选择reset, 选择sell)
含义是:今天我没有股票,有两种情况:
1是我昨天就没有持有,今天选择reset,所以今天还是没有持有
2是我昨天持有股票,但是我今天sell了,所以今天没有股票了
dp[i][k][1] = max(dp[i-1][k][0],dp[i-1][k-1][0]-prices[i])
max(选择reset, 选择buy)
含义是:今天我持有股票,有两种可能:
1是我昨天持有股票,但是今天选择reset,所以我今天还是持有股票
2是我昨天没有股票,但是我选择buy,所以我今天就持有股票了
如果buy,就要从利润中减去prices[i],如果sell,就要在利润中增加prices[i],今天得最大利润就是这两种可能中选择较大的那个,而且要注意k的限制,如果买入,k的值要减1。
- 初始条件
dp[-1][k][0] = 0
因为i是从0开始的,所以i=-1意味着还没有开始,这时候的利润是0
dp[-1][k][1] = -infinity
这时候还没有开始,是不可能持有股票的,用负无穷表示不可能
dp[i][0][0] = 0
因为k最小应该为1,所以k=0表示不能交易,此时利润当然是0
dp[i][0][1] = -infinity
在不允许交易的情况下,是不可能持有股票的,用负无穷表示不可能
把上面的状态转移方程总结一下:
base case:
dp[-1][k][0] = dp[i][]0[0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity
状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])
dp[i][k][1] = max(dp[i-1][k][0],dp[i-1][k-1][0]-prices[i])
- 解决题目
121题,k=1
直接套用状态方程,根据base case,做一些简化:
dp[i][1][0] = max(dp[i-1][1][0],dp[i-1][1][1]+prices[i])
dp[i][1][1] = max(dp[i-1][1][1],dp[i-1][0][0]-prices[i])
解释:k=0的base case,所以dp[i-1][0][0] = 0
k都是1,不会改变,所以k对状态转移已经没有影响了,可以简化去掉k
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
直接写出代码:
n = len(prices)
dp = [[0*n] for _ in range(2)]
dp[-1][0] = 0
dp[-1][1] = -inf
for i in range(1,n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],-prices[i])
# dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
# = max(-infinity,0-prices[i])
# 因为只能买卖一次,因此持有状态下,只能和当前价格对比,不能加上之前的状态
return dp[-1][0]
122题
k=+infinity
如果k是无穷大,那k=1和k是一样的,因此k的状态也就不需要记录了。
n = len(prices)
dp = [[0]*2 for _ in range(n)]
dp[-1][0] = 0
dp[-1][1] = -inf
for i in range(0,n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
return dp[n-1][0]
123 K=2
前面的题都与k无关,或者可以简化,这题中对k的处理就很重要了,也要在k的范围内进行穷举
n = len(prices)
dp = [[0]*3 for _ in range(n)]
for i in range(n):
for k in range(K):
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])
dp[i][k][1] = max(dp[i-1][k][0],dp[i-1][k-1][0]-prices[i])
return dp[-1][K][0]
这里k的取值范围比较小,可以直接列举
在这里插入代码片
188 k为ang integer
n = len(prices)
dp = [[0]*3 for _ in range(n)]
dp[i][2][0] = 0,dp[i][1][0] = 0
dp[i][2][1] = -inf,dp[i][1][1] = -Inf
for i in range(n):
for k in range(K):
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])
dp[i][k][1] = max(dp[i-1][k][0],dp[i-1][k-1][0]-prices[i])
return dp[-1][K][0]
309 K=-infinity 含冷静期
每次sell完之后,都需要等一天才能继续交易,把这个特点融入上一题的状态转移方程即可,第i天选择买入之后,要从第i-2的状态转移,而不是i-1。
n = len(prices)
dp = [[0]*2 for _ in range(n)]
dp[-1][1] = -prices[0]
for i in range(n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-2][0]-prices[i])
return dp[-1][0]
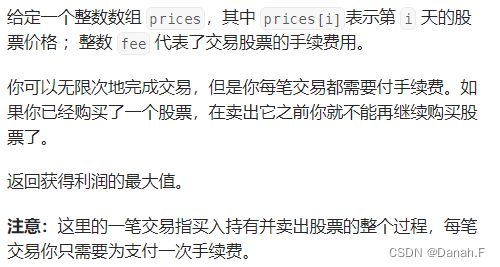
714 K=-infinity 含手续费
每次交易需要手续费时,只需要从利润中减去即可,相当于买入股票的价格升高了 。
n = len(prices)
dp = [[0]*2 for _ in range(n)]
dp[-1][0] = 0
dp[-1][1] = -inf
for i in range(0,n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]-fee)
return dp[n-1][0]
122 买卖股票的最佳时机II
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
profit = 0 # 记录利润
for i in range(1, len(prices)):
if prices[i] > prices[i-1]:
profit += prices[i] - prices[i-1]
# print(profit)
return profit
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0]*2 for _ in range(n)]
dp[-1][0] = 0
dp[-1][1] = -inf
for i in range(0,n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
return dp[n-1][0]
123 买卖股票的最佳时机III
188 买卖股票的最佳时机IV
309 最佳买卖股票实际含冷冻期
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0]*2 for _ in range(n)]
dp[-1][1] = -prices[0]
for i in range(n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-2][0]-prices[i])
return dp[-1][0]
714 买卖股票的最佳时机含手续费
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
n = len(prices)
dp = [[0]*2 for _ in range(n)]
dp[-1][0] = 0
dp[-1][1] = -inf
for i in range(0,n):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]-fee)
return dp[n-1][0]
70 爬楼梯
class Solution:
def climbStairs(self, n: int) -> int:
f = [0]*(n+1)
f[0] = 1
f[1] = 1
for i in range(2,n+1):
f[i]=f[i-1]+f[i-2]
return f[-1]
279 完全平方数
class Solution:
def numSquares(self, n: int) -> int:
def isP(num):
return num**0.5 == int(num**0.5)
dp = [10001]*(n+1)
dp[0] = 0
for i in range(n):
if isP(i+1):
for j in range(i+1,n+1):
dp[j] = min(dp[j],dp[j-(i+1)]+1)
return dp[-1]
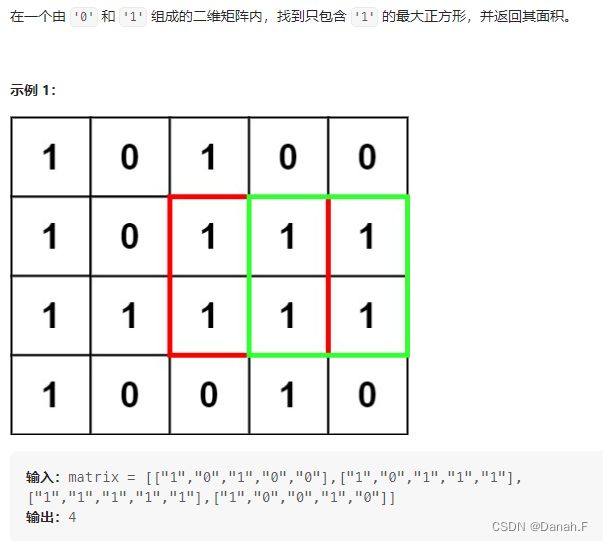
221 最大正方形
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
rows,columns = len(matrix),len(matrix[0])
if rows == 0 or columns == 0:
return 0
dp = [[0]*columns for _ in range(rows)]
maxSizes = 0
for i in range(rows):
for j in range(columns):
if matrix[i][j] == '1':
if i==0 or j==0:
dp[i][j] = 1;
else:
dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
maxSizes = max(maxSizes,dp[i][j])
maxSqures = maxSizes*maxSizes
return maxSqures
4.10 查找
4.10.1 常见查找算法
4.10.1.1 算法
4.10.1.2 练习题
4.11 排序
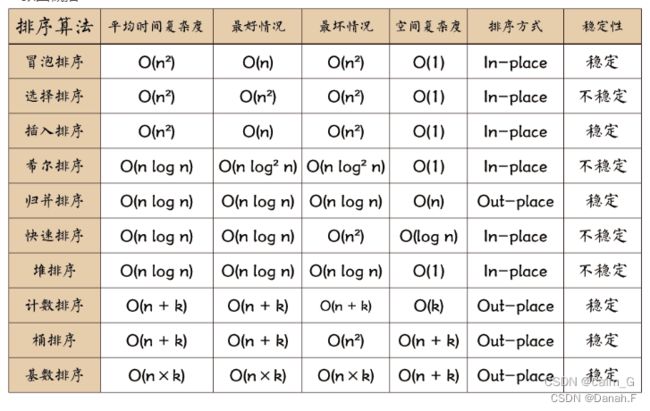
4.11.1 常见排序算法
几种最经典、最常用的排序方法:冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、计数排序、基数排序、桶排序、堆排序。
4.11.1.1 时间复杂度
4.11.1.2 如何分析一个排序算法
<1> 算法的执行效率
- 最好、最坏、平均情况时间复杂度。
- 时间复杂度的系数、常数和低阶。
- 比较次数,交换(或移动)次数。
<2>算法的稳定性
稳定性是指:如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
<3>排序算法的内存损耗
原地排序算法:特指空间复杂度是O(1)的排序算法。
4.11.2 冒泡排序
4.11.2.1 算法
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。假设长度为n的数组arr,要按照从小到大排序。则冒泡排序的具体过程可以描述为:首先从数组的第一个元素开始到数组最后一个元素为止,对数组中相邻的两个元素进行比较,如果位于数组左端的元素大于数组右端的元素,则交换这两个元素在数组中的位置。这样操作后数组最右端的元素即为该数组中所有元素的最大值。接着对该数组除最左端的n-1个元素进行同样的操作,再接着对剩下的n-2个元素做同样的操作,直到整个数组有序排列。
4.11.2.2 练习题
代码
#include 4.11.3 选择排序
4.11.3.1 算法
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。具体来说,假设长度为n的数组arr,要按照从小到大排序,那么先从n个数字中找到最小值min1,如果最小值min1的位置不在数组的最左端(也就是min1不等于arr[0]),则将最小值min1和arr[0]交换,接着在剩下的n-1个数字中找到最小值min2,如果最小值min2不等于arr[1],则交换这两个数字,依次类推,直到数组arr有序排列。算法的时间复杂度为O(n^2)。
4.11.3.2 练习题
代码
void swap(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
void Selection_Sort(int arr[], int length)
{
for(int i=0;i<length;i++)
{
int min = i;
for(int j=i+1;j<length;j++)
{
if(arr[j]<arr[min])
{
min = j;
}
}
swap(&arr[min],&arr[i]);
}
}
4.11.4 插入排序
4.11.4.1 算法
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。例如要将数组arr=[4,2,8,0,5,1]排序,可以将4看做是一个有序序列,将[2,8,0,5,1]看做一个无序序列。无序序列中2比4小,于是将2插入到4的左边,此时有序序列变成了[2,4],无序序列变成了[8,0,5,1]。无序序列中8比4大,于是将8插入到4的右边,有序序列变成了[2,4,8],无序序列变成了[0,5,1]。以此类推,最终数组按照从小到大排序。该算法的时间复杂度为O(n^2)。
4.11.4.2 练习题
代码
void insertion_sort(int arr[],int len)
{
int i,j;
for(i=1;i<len;i++)
{
int key = arr[i];
j = i-1;
while((j>=0) && (arr[j]>key))
{
arr[j+1] = arr[j]; //当arr[j]小于key时,将有序序列后移一位,给key值留位置
j--;
}
arr[j+1] = key; //找到位置后,将key放在该位置
}
}
4.11.5 希尔排序
4.11.5.1 算法
希尔排序(Shell’s Sort)在插入排序算法的基础上进行了改进,算法的时间复杂度与前面几种算法相比有较大的改进,但希尔排序是非稳定排序算法。其算法的基本思想是:先将待排记录序列分割成为若干子序列分别进行插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行一次直接插入排序。该算法时间复杂度为O(n log n)。
步骤:
1.将数组按照步长gap(元素的间隔)分组,对每组记录采用插入排序的方法进行排序
2.随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。
4.11.5.2 练习题
代码
void shell_sort(int arr[], int len)
{
int i, j, k, gap;
for(gap = len/2;gap>0;gap/=2)
{
for(i=0;i<gap;i++)
{
for(j=i+gap;j<len;j+=gap)
{
if(arr[j]<arr[j-gap])//如果a[j]
{
int temp = arr[j];//后面是插入排序的过程,将每组按照插入排序排成有序序列。
k = j-gap;
while(k>=0 && arr[k]>temp)
{
arr[k+gap] = arr[k];
k-=gap;
}
arr[k+gap] = temp;
}
}
}
}
}
4.11.6 归并排序
4.11.6.1 算法
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。代价是需要额外的内存空间。若将两个有序表合并成一个有序表,称为2-路归并。 该算法时间复杂度为O(n log n)。
步骤:
- 将长度为n的输入序列分为两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排好序的子序列合并成一个最终的排序序列。
4.11.6.2 练习题
代码
void MergeSort(*int arr[], int start, int end, int* temp)
{
if(start>=end)
return;
int mid=(start+end)/2;
MergeSort(arr,start,mid,temp);
MergeSort(arr,mid+1,end,temp);
//合并两个有序序列
int length = 0;
int i_start = start;
int i_end = mid;
int j_start = mid+1;
int j_end = end;
while(i_start <= i_end && j_start <= j_end)
{
if(arr[i_start]<arr[j_start])
{
temp[length] = arr[i_start];
length++;
i_start++;
}
else
{
temp[length] = arr[j_start];
length++;
j_start++;
}
while(i_start<=i_end)
{
temp[length] = arr[i_start];
length++;
i_start++;
}
while(j_start <= j_end)
{
temp[length] = arr[j_start];
length++;
j_start++;
}
//把辅助空间的数据放到原空间
for(int i=0;i<length;i++)
{
arr[start+i] = temp[i];
}
}
}
4.11.7 快速排序
4.11.7.1 算法
快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。快速排序的基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,已达到整个序列有序。一趟快速排序的具体过程可描述为:从待排序列中任意选取一个记录(通常选取第一个记录)作为基准值,然后将记录中关键字比它小的记录都安置在它的位置之前,将记录中关键字比它大的记录都安置在它的位置之后。这样,以该基准值为分界线,将待排序列分成的两个子序列。它是处理大数据最快的排序算法之一了。该算法时间复杂度为O(n log n)。
4.11.7.2 练习题
4.11.8 堆排序
4.11.8.1 算法
4.11.8.2 练习题
4.12 查找算法
4.12.1 顺序查找
4.12.1.1 算法
顺序查找适合于存储结构为顺序存储或链式存储的线性表。
顺序查找就是从数据结构线性表的一端开始,顺序扫描。依次将扫描到的结点关键字与给定的k值相比较,若相等,则查找成功;若扫描到最后仍没有找到等于k的节点,表示查找失败。
平均复杂度为:1/n*(1+2+3+…+n) = (n+1)/2,所以时间复杂度为O(n)。
4.12.1.2 练习题
代码
int search(int arr[], int value, int len)
{
for(int i=0;i<len;i++)
{
if(arr[i] == value)
return i;
}
return;
}
4.12.2 二分查找
4.12.2.1 算法
二分查找,数据必须是有序的,如果无序需要先进行排序操作。
二分查找也叫折半查找,属于有序查找算法。用给定的值先跟中间节点的关键字比较,中间节点把线性表分为两个子表,若相等则查找成功;若不相等,根据给定的值与中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到找到或者表中没有这样的结点。
复杂度分析:平均时间复杂度为O(log2n)
4.12.2.2 练习题
代码
int Binary(int arr[], int value, int low, int high)
{
int mid = low+(high-low)/2;
if(arr[mid] == value)
return mid;
if(arr[mid] > value)
return Binary(arr, value, low, mid-1);
if(arr[mid] < value)
return Binary(arr, value, mid+1, high);
}
//递归
int BinarySearch(int arr[], int value, int n)
{
int low,high,mid;
low = 0;
high = n-1;
while(low<=high)
{
mid = low+(high-low)/2;
if(arr[mid] == value)
return mid;
if(arr[mid] > value)
high = mid-1;
if(arr[mid] < value)
low = mid+1;
}
}
4.12.3 插值查找
4.12.3.1 算法
二分查找是从中间点查找,而插值查找是在二分查找的基础上将查找点改进为自适应选择,可以提高查找效率。
对于表比较大且数据分布比较均匀的表来说,插值查找的平均性能比二分查找高。,而对于分布不均匀的数据来说,插值查找可能不是最好的选择。
复杂度分析:平均复杂度为O(log2(log2n)),最好是O(1),最差是O(n)。
m i d = l o w + h i g h − l o w 2 mid = low+\frac{high-low}{2} mid=low+2high−low
m i d = l o w + ( h i g h − l o w ) k e y − a [ l o w ] a [ h i g h ] − a [ l o w ] mid = low+(high-low)\frac{key-a[low]}{a[high]-a[low]} mid=low+(high−low)a[high]−a[low]key−a[low]
4.12.3.2 练习题
代码
int InsertionSearch(int arr[], int value, int low, int high)
{
int mid = low+(high-low)*(value-arr[low])/(arr[high]-arr[low]);
if(arr[mid] == value)
return mid;
if(arr[mid] > value)
return InsertionSearch(arr, value, low, mid-1);
if(arr[mid] < value)
return InsertionSearch(arr, value, mid+1, high);
}
4.13 贪心算法
4.13.1 算法
4.13.2 例题
322 零钱兑换
# 动态规划
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
n = len(coins)
dp = [float('inf')]*(amount+1)
dp[0] = 0
for i in range(n):
x = coins[i]
for j in range(x,amount+1):
dp[j] = min(dp[j],dp[j-x]+1)
print(f"dp[{j}]:{dp[j]}",)
return dp[amount] if dp[amount]!=float('inf') else -1
1217 玩筹码
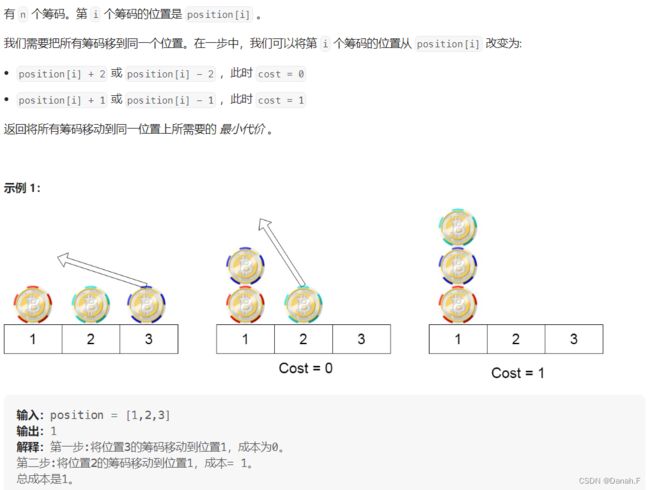
从奇数(偶数)到奇数(偶数)位置,最小开销为0;从偶数(奇数)到奇数(偶数)位置,最小开销为1。所以结果分为两种,一种是全部到偶数位置,则开销为奇数位置的个数,一种是全部移到奇数位置,则开销为偶数位置的个数,所以最后转化为奇数和偶数的个数的最小值。
class Solution:
def minCostToMoveChips(self, position: List[int]) -> int:
cnt = 0
for i in position:
if i%2 == 0:
cnt += 1
return min(cnt,len(position)-cnt)
55 跳跃游戏

初始化最远位置为 0,然后遍历数组,如果当前位置能到达,并且当前位置+跳数>最远位置,就更新最远位置。最后比较最远位置和数组长度。
class Solution:
def canJump(self, nums: List[int]) -> bool:
max_i = 0
for i,num in enumerate(nums):
if max_i >= i and i+num > max_i:
max_i = i + num #更新最远距离
return max_i>=i
华为od 最大利润、贪心的商人
num = int(input())
days = int(input())
item = list(map(int,input().split()))
prices = []
ans = 0
for line in sys.stdin:
a = list(map(int,input().split()))
prices.append(a)
for i in range(1,num):
for j in range(1,days):
if prices[i][j] > prices[i][j-1]:
ans += (prices[i][j]-prices[i][j-1])*item[i]
print(ans)
4.14 其他
HJ28 素数伴侣
import math
def check(num): #判断是否是素数
for i in range(2,int(math.sqrt(num)) + 2): #除去1和本身的数没有其他的因子称为素数,但其实检验到int(math.sqrt(num)) + 1即可(数学证明略),不然会超时
if(num % i == 0):
return False
return True
def find(odd, visited, choose, evens): #配对的过程
for j,even in enumerate(evens):
if check(odd+even) and not visited[j]: #如果即能配对,这两个数之前没有配过对(即使两个不能配对visit值为0,但是也不能过是否是素数这一关,所以visit就可看为两个能配对的素数是否能配对)
visited[j] = True #代表这两个数能配对
if choose[j]==0 or find(choose[j],visited,choose,evens): #如果当前奇数没有和任何一个偶数现在已经配对,那么认为找到一组可以连接的,如果当前的奇数已经配对,那么就让那个与之配对的偶数断开连接,让他再次寻找能够配对的奇数
choose[j] = odd #当前奇数已经和当前的偶数配对
return True
return False
while True:
try:
num = int(input())
a = input()
a = a.split()
b = []
count = 0
for i in range(len(a)):
a[i] = int(a[i])
evens = []
odds = []
for i in a: #将输入的数分为奇数和偶数
if(i % 2 == 0):
odds.append(i)
else:
evens.append(i)
choose = [0]*len(evens) #choose用来存放当前和这个奇数配对的那个偶数
for odd in odds:
visited = [False]*len(evens) #visit用来存放当前奇数和偶数是否已经配过对
if find(odd,visited,choose,evens):
count += 1
print(count)
except:
break
HJ108 最小公倍数
import sys
input_num = input().split()
a=int(input_num[0])
b=int(input_num[1])
if a<b:
a,b=b,a
ji = a*b
for i in range(min(a,b),ji+1,min(a,b)):
if i % max(a,b) == 0:
print(i)
HJ25 数据分类处理
import sys
I = input().split()
R = list(map(int,input().split()))
I_n = int(I[0])
I_list = I[1:]
R_n = R[0]
R_list = R[1:]
R_sort = list(sorted(set(R[1:])))
R_sort = list(map(str,R_sort))
# print(R_sort)
count = 0
res = []
for i in range(len(R_sort)):
num = 0
for j in range(len(I_list)):
if R_sort[i] in I_list[j]:
num += 1
if num == 0:
continue
res.append(R_sort[i]) #将r放进结果中
res.append(str(num))
for j in range(len(I_list)):
if R_sort[i] in I_list[j]:
res.append(str(j))
res.append(I_list[j])
res.insert(0,str(len(res)))
print(' '.join(res))
计数质数
![]()
# 暴力法,超时
class Solution:
def isPrime(self,n):
for i in range(2,int(n**0.5)+1):
if n%i == 0:
return 0
return 1
def countPrimes(self, n: int) -> int:
count = 1
if n<3:
return 0
for i in range(2,n):
if i%2 != 0:
if self.isPrime(i)==1:
count += 1
return count
# 厄拉多塞筛法
# 每次排除选择质数的数字的倍数
class Solution:
def countPrimes(self, n: int) -> int:
count = 0
sign = [0]*n #标志设为0
for i in range(2, n):
if sign[i] == 0:
count += 1
for j in range(i+i,n,i):#对于倍数,标志置为1
sign[j] = 1
return count
NC61 两数之和
# 暴力法,超时
class Solution:
def twoSum(self , numbers: List[int], target: int) -> List[int]:
# write code here
for i in range(len(numbers)):
for j in range(i+1,len(numbers)):
if numbers[i]+numbers[j] == target:
return i+1,j+1
# 使用哈希表,以空间换时间
class Solution:
def twoSum(self , numbers: List[int], target: int) -> List[int]:
# write code here
dict = {}
for i in range(len(numbers)):
dict[numbers[i]] = i
for i in range(len(numbers)):
if target-numbers[i] in dict:
index = dict[target-numbers[i]]+1
if i+1 == index:
continue
else:
return i+1,index
合并区间
# class Interval:
# def __init__(self, a=0, b=0):
# self.start = a
# self.end = b
#
# 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
#
#
# @param intervals Interval类一维数组
# @return Interval类一维数组
#
class Solution:
def merge(self , intervals: List[Interval]) -> List[Interval]:
# write code here
if not intervals:
return []
intervals = sorted(intervals,key=lambda intervals:intervals.start)
out = []
out.append(intervals[0])
for i in range(1,len(intervals)):
last = out[-1]
# print(last)
cur_left,cur_right = intervals[i].start,intervals[i].end
if last.end<cur_left:
out.append(intervals[i])
else:
last.end = max(last.end,cur_right)
return out
华为od 最大版本号
def compare()
{
a = input()
a_s = a.split('.')
b = input()
b_s = b.split('.')
for i in range(2):
v1 = int(a_s[i])
v2 = int(b_s[i])
if v1 != v2:
return v1>v2?a:b
if len(v1)>2 and len(v2)>2:
a1 = a_s[2].split('-')
b2 = b_s[2].split('-')
a_int = a1[0]
b_int = b2[0]
if a_int != b_int:
return a_int>b_int?a:b
if len(a1)>=2 and len(b2)>=2:
#有里程碑版本
return ord(a1[1]) > ord(b2[1])?a:b
else:
# 至少有一个没有里程碑版本
return len(a1)>len(b2)?a:b
else:
return len(v1)>len(v2)?a:b
}
哈希表:某个字符在数组里出现的次数
第几大:堆
有序时:对撞指针
找到所有的:回溯法
遍历查询某个值:可以通过赋值防止被再次遍历
参考链接:手把手带你刷Leetcode力扣
数据结构与算法学习笔记
常用十大排序算法
七大查找算法
华为OD机试真题2023_Swift_100_获取最大软件版本号