论文解读：LaMa:Resolution-robust Large Mask Inpainting with Fourier Convolutions

论文：https://arxiv.org/pdf/2109.07161.pdf

代码： GitHub - advimman/lama: LaMa Image Inpainting, Resolution-robust Large Mask Inpainting with Fourier Convolutions, WACV 2022

目录

1  摘要：

2  主要贡献：

3 方法

 3.1 网络前层的全局上下文

 3.2 快速傅里叶卷积

3.3 快速傅里叶网络pytorch实现

---

1  摘要：

2  主要贡献：

3  方法

 3.1 网络前层的全局上下文

 3.2 快速傅里叶卷积

---

如上图，本文方法能够成功修复大区域，并且在处理各种图像时表现良好，包括那些具有复杂重复结构的图像。该方法能够适应高分辨率图像，尽管仅在低分辨率256×256的训练下进行。

1  摘要：

        尽管现代图像修复系统取得了显著的进展，但它们经常在处理大面积缺失区域、复杂几何结构和高分辨率图像时遇到困难。主要原因之一是修复网络和损失函数缺乏有效的感受野。

因此本文提出了一种名为大掩蔽修复（LaMa）的新方法。

    LaMa基于以下几点：

 i）使用快速傅里叶卷积（FFC）的新修复网络架构，具有全图感受野；

 ii）具有高感受野的感知损失；

 iii）使用大型训练掩蔽，释放前两个组件的潜力。

2  主要贡献：

i）提出了一种基于快速傅里叶卷积（FFC）[Fast fourier convolution ]的修复网络。

  FFC允许在网络的早期层中覆盖整个图像的感受野。FFC的这个特性提高了网络的感知质量和参数效率。有趣的是，FFC的归纳偏差使网络能够推广到在训练过程中从未见过的高分辨率图像。这一发现带来了重要的实际效益，因为需要更少的训练数据和计算。

ii）使用具有高感受野的语义分割网络的感知损失[Perceptual losses for real-time style transfer and super-resolution]。

基于经验，不仅修复网络的感受野不足，感知损失也受到影响。本文的损失设计促进了全局结构和形状的一致性。

iii）我们引入了一种训练掩膜生成的积极策略，以发挥前两个组件的高感受野的潜力。该过程生成宽大的掩膜，迫使网络充分利用模型和损失函数的高感受野。

LaMa的主要组成部分是具有高感受野的架构

（i）具有高感受野损失函数

（ii）积极的训练掩膜生成算法

（iii）通过评估，LaMa可以在仅在低分辨率数据上进行训练后推广到高分辨率图像。LaMa可以捕捉和生成复杂的周期性结构，并且对于大面具具有稳健性。此外，与竞争基准相比，LaMa所需的可训练参数和推断时间成本显著减少。

3 方法

        目标是对由未知像素的二进制掩码 m 掩盖的彩色图像 x 进行修复，被掩码的图像表示为 x ⊙ m。掩码 m 与被掩码的图像 x ⊙ m 堆叠在一起，形成一个四通道的输入张量 x ′ = stack(x ⊙ m,m)。我们使用一个前馈式修复网络 f θ (·)，也称为生成器。给定 x ′，修复网络以完全卷积的方式处理输入，并生成修复后的三通道彩色图像 x ˆ = f θ (x ′)。训练是在从真实图像和合成的掩码获得的（图像，掩码）对的数据集上进行的。

 3.1 网络前层的全局上下文

在具有挑战性的情况下，例如填充大型掩码，正确的修复需要考虑全局上下文。因此，一个良好的架构应该在pipline的尽早阶段具有尽可能宽广的感受野。

传统的全卷积模型，例如 ResNet [14]，由于通常采用小型（例如3×3）的卷积核，其感受野增长缓慢 [29]。感受野可能不足，特别是在网络的早期层中，导致许多层缺乏全局上下文，并浪费计算和参数来创建全局上下文。

对于宽广的掩码，生成器在特定位置的整个感受野可能在掩码内，因此只能观察到缺失的像素。对于高分辨率图像，这个问题尤为显著。

 3.2 快速傅里叶卷积

快速傅里叶卷积（FFC）[4]是最近提出的运算符，它允许在早期层中使用全局上下文。FFC基于通道级的快速傅里叶变换（FFT），具有覆盖整个图像的感受野。

FFC将通道分为两个并行分支：

i）本地分支使用常规卷积

ii）全局分支使用实值FFT来考虑全局上下文。

实值FFT只能应用于实值信号，而逆实值FFT确保输出是实值的。与FFT相比，实值FFT仅使用了一半的频谱。具体而言，FFC的步骤如下：

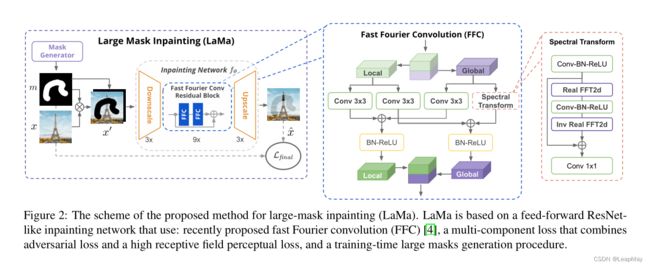
 最后，本地分支（i）和全局分支（ii）的输出被融合在一起。FFC的示意图如图2所示

 图2：用于大掩膜修复（LaMa）方法的方案。LaMa基于一个前馈的类ResNet修复网络，使用了最近提出的快速傅里叶卷积（FFC），一个结合了对抗损失和高接受域感知损失的多组分损失，以及一个训练时生成大掩膜的过程。

FFC具有全可微性和易于使用的特点，可完全替代传统的卷积操作。由于具有图像全局接受域，FFC允许生成器从早期层开始考虑全局上下文，这对于高分辨率图像修复至关重要。这也导致更好的效率：可训练参数可以用于推理和生成，而不是“等待”信息传播。

FFC与普通卷积相比，计算成本相当，但当普通卷积使用大核卷积时，FFC体现了优越性，在频谱转换器时仍然使用1×1的核来学习全局感受野。

实验证明FFC非常适合捕捉周期性结构，这在人造环境中非常常见，例如砖块、梯子、窗户等（图4）。有趣的是，过在所有频率上共享相同的卷积操作，模型具有尺度等变性[4]（图5、6）。

3.3 快速傅里叶网络pytorch实现

以下示例中，定义了一个名为FFTConvNet的类，它继承自nn.Module。类的构造函数中定义了频域卷积的权重参数（实部和虚部），并实现了前向传播函数。在前向传播函数中，输入数据首先通过fft.fftn函数转换为频域表示，然后进行频域上的卷积计算，最后通过fft.ifftn函数将频域卷积结果转换回时域。在计算过程中，需要注意处理实部和虚部的乘法和加法运算。最后，加上偏置并应用激活函数（这里使用ReLU）得到最终的输出。

这只是一个简单的示例，实际的FFT卷积网络可能需要更多的层和参数调整来适应具体的任务。但这个示例可以作为一个起点，帮助你理解如何在PyTorch中实现FFT卷积网络。

import torch
import torch.nn as nn
import torch.fft as fft

class FFTConvNet(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size):
        super(FFTConvNet, self).__init__()
        self.kernel_size = kernel_size
        self.padding = kernel_size // 2  # 保持输出与输入大小相同的padding

        # 定义频域卷积的参数，使用实部和虚部表示
        self.weight_real = nn.Parameter(torch.Tensor(out_channels, in_channels, kernel_size, kernel_size))
        self.weight_imag = nn.Parameter(torch.Tensor(out_channels, in_channels, kernel_size, kernel_size))
        self.bias = nn.Parameter(torch.Tensor(out_channels))

        self.reset_parameters()

    def reset_parameters(self):
        nn.init.kaiming_uniform_(self.weight_real, a=math.sqrt(5))
        nn.init.kaiming_uniform_(self.weight_imag, a=math.sqrt(5))
        if self.bias is not None:
            fan_in, _ = nn.init._calculate_fan_in_and_fan_out(self.weight_real)
            bound = 1 / math.sqrt(fan_in)
            nn.init.uniform_(self.bias, -bound, bound)

    def forward(self, x):
        # 将输入数据转换为频域表示
        x_freq = fft.fftn(x, dim=(-2, -1))

        # 获取权重的实部和虚部
        weight_real = self.weight_real.unsqueeze(2).unsqueeze(3)
        weight_imag = self.weight_imag.unsqueeze(2).unsqueeze(3)

        # 计算频域上的卷积
        conv_real = torch.sum(x_freq.real.unsqueeze(1) * weight_real - x_freq.imag.unsqueeze(1) * weight_imag, dim=(-3, -2))
        conv_imag = torch.sum(x_freq.real.unsqueeze(1) * weight_imag + x_freq.imag.unsqueeze(1) * weight_real, dim=(-3, -2))

        # 将频域卷积结果转换回时域
        conv = fft.ifftn(conv_real + 1j * conv_imag, dim=(-2, -1)).real

        # 添加偏置并应用激活函数
        conv = conv + self.bias.view(1, -1, 1, 1)
        conv = torch.relu(conv)

        return conv


# 使用示例
in_channels = 3
out_channels = 64
kernel_size = 3

input_data = torch.randn(1, in_channels, 32, 32)
model = FFTConvNet(in_channels, out_channels, kernel_size)
output = model(input_data)
print(output.shape)