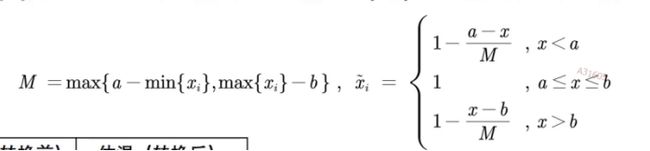数学建模综合评价方法
数学建模学习
综合评价总结1
总结分析:
1.层次分析法(AHP)
(不做讨论)
2.Topsis方法(处理多方案打分的问题)
(优点:数据多与少都可以分析,在系统数据资料较少和条件不满足统计要求的情况下,更具有实用性。
缺点:要求样本数据且具有时间序列特性,只是对评判对象的优劣做出鉴别,并不反映绝对水平,具有“相对评价”的全部缺点)
)
3.基于灰色关联度的灰色综合评价法(处理多方案打分的问题)
(优点:原理简单,能同时进行多个对象评价,计算快捷,结果分辨率高、评价客观,具有较好的合理性和适用性,实用价值较高
缺点:只能国赛,只能反映各评价对象内部的相对接近度,并不能反映与理想的最优方案的相对接近程度(我的理解是只能判断已有方案那个最好,不能得出最优方案)
)
4.模糊综合评判法(有数据用,没数据时间不够最好不用)【方案选取型】【等级评价型】
(优点:可对涉及模糊因素的对象系统进行综合评价
缺点:它并不能解决评价指标间相关造成的评价信息重复问题,隶属函数的确定还没有系统的方法,而且合成的算法也有待进一步探讨。其评价过程大量应用了人的主观判断,由于各因素权重的确定带有一定的主观性,因此,总的来说,模糊综合评判是-种基于主观信息的综合评价方法。实践证明,综合评价结果的可靠性和准确性依赖于合理选取因素,因素的权重分配和综合评价的合成算子等。所以,无论如何,都必须根据具体综合评价问题的目的、要求及其特点,从中选出合适的评价模型和算法﹐使所做的评价更加客观、科学和有针对性。
)
5…
权重确定法:
1.专家咨询权数法(包括在层次分析法中)
2.因子分析权数法
3.信息量权数法
4.独立性权数法
5.主成分分析法(降维的,不能综合评价)
6.层次分析法(不用)
7.灰色关联度分析法:
(优点:数据多与少都可以分析,在系统数据资料较少和条件不满足统计要求的情况下,更具有实用性。
缺点:缺点是要求样本数据且具有时间序列特性。当然,该方法只是对评判对象的优劣做出鉴别,并不反映绝对水平。而且,基于灰色关联系数的综合评价具有“相对评价”的全部缺点。另外,灰色关联系数的计算还需要确定“分辨率”,而它的选择并没有一个合理的标准。需要说明的是,应用该种方法进行对象评价时指标体系及权重分配也是一个关键问题,选择的恰当与否直接影响最终评价结果。)
8.熵权法(可以用这个打比赛,需要数据)
9…
建模步骤:
步骤1:原始矩阵(原数据)正向化:
(使不同指标的指标值与他们的影响好坏的对应关系相一致)
(极小型(成本型)指标,中间型指标,区间型指标------》极大型(效益型)指标)
极小型:
中间型:
区间型:
步骤二:正向化矩阵标准化(数据预处理):
(消除不同指标量纲的影响)
1.

2.但如果这种标准化之后Zij里有负数,则用另一种标准化:
3.灰色相关分析的标准化:原矩阵/均值
步骤三:计算权重:
(根据情况选用不同方法)
步骤四:计算得分并归一化:
(不同的评价方法不同的公式)
综合分析方法:
1.层次分析法:
一种主观性很强的人为赋予各指标权重进行线性加得到方案期待值即得分的方法,在其他综合评价方法计算权重的地方也有引用,可以改进为其他加权方法.
(舍弃它)
(只会影响到指标最高和最低的两个样本在这个指标上的评分,并且因为实际我们遇到的问题往往是多指标问题,这种影响也就被缩小了很多)
)
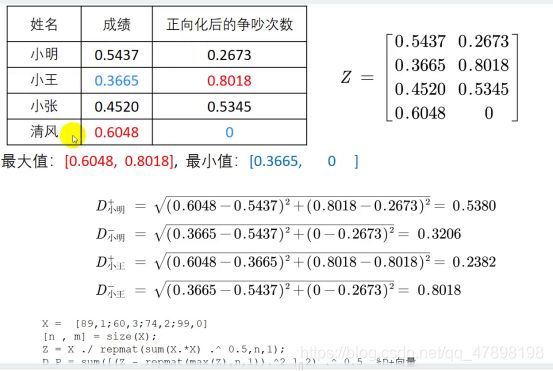
概况:1.计算出每一列即每种指标的最大值和最小值Nmax和Nmin
2.分别计算出每种方案的所有指标与各指标(每一列)的Nmax和Nmin的欧氏距离的距离平方Smax和Smin.
3.用层次分析法赋予每个方案(行)的每个指标的Smax和Smin一个权重
(也就是有多少个指标,就对应多少个权重)
4.算出每个方案的D+,D-后得出评分,最后归一化得分(所有方案得分相加得1)
优化权重:
熵权法:1.用标准化之后的矩阵计算出一个矩阵,当做概率矩阵:

2.计算出信息效用值和熵权:
3.灰色关联分析:
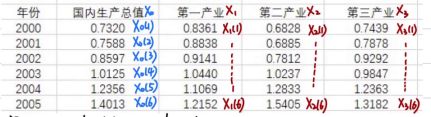
1.数据预处理后,提取数据每行最大值为一列作为母序列,其他指标为子序列
2.对于子序列每个值取对应的母序列的值和自身的差作为一个新矩阵
3.选定子序列中值最小的设为a(两级最小差),值最大的为b(两极最大差)
4.计算每个指标的每个值的灰色关联度,每种指标取平均即为这种指标的灰色关联度
5.将每种指标的灰色关联度转换为权重,之后求和并归一化得到每种方案的得分:
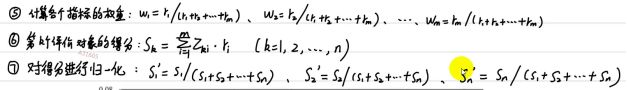
4.模糊综合评价:
等级型:对各等级设定隶属函数
方案型:对各指标设定隶属函数
【等级评价型】
(用的话最好给出各等级的区间,否则就需要模糊统计(主观性弱)耗时太久不用)
(如果有数据的话可以用熵权法确定权重)
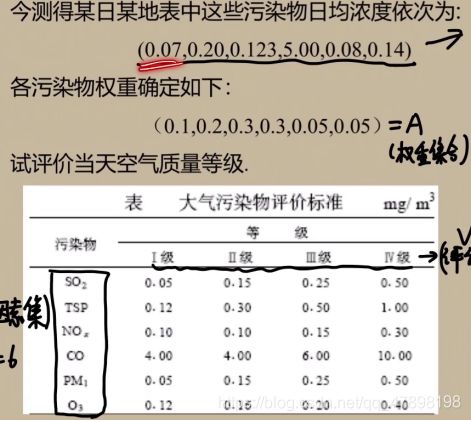
大致步骤:
每个指标在不同等级上区间是不同的,若赛题给出每个指标在不同等级上的区间,则可以用这种方法,否则使用其他方法太耗时。
可以试试能不能爬到这些指标在不同等级上的标准
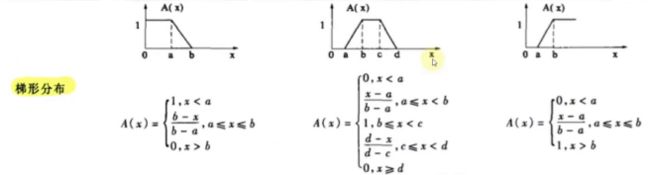
1.判断各等级的类型,用梯形分布(或者其他分布)做出每个等级的隶属函数
(把模糊的各等级概念用不同的连续线性函数表示出来)
用来将传进来的数据每个指标和对应的a,b(区间)给这些函数,得到这个指标在每个等级的隶属度
A为权重集,多少个指标多少个权重
如果没给权重集,有数据用熵权法求,没数据用层次分析法或者按赛题具体分析看能不能默认他们权重相等

最后结果即为B中隶属度最大的等级
【方案型】
如果没有给权重集,用给的数据算权重集,没给按情况判断是否可以默认权重相等
1.判断指标的数据类型,根据已有的尺度设计隶属函数
(不唯一,也可以按照梯度分布等或者文章查阅,专家意见,合理即可)

2.将数据带入函数得到不同方案所对应的不同隶属度,即为单因素评判矩阵
3.权重集和评判矩阵相乘得到B,即为各方案对最佳方案的隶属度