回顾分类决策树相关知识并利用python实现
大家好,我是带我去滑雪!
决策树(Decision Tree)是一种基本的分类与回归方法,呈树形结构,在分类问题中,表示预计特征对实例进行分类的过程。它可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。
结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。从根节点开始,对样本数据某一个特征进行测试,根据测试结果,将对应样本分配到子节点上,形成两个或者多棵子树,然后再对每一棵子树重复同样的过程,直到样本数据分到某个叶子节点。简单来说,决策树就是通过一系列规则对数据进行分类的过程。
目录
1、如何构建决策树?
2、特征选择
3、决策树生成
4、决策树剪枝
5、实现决策树案例1—自定义函数
(1)导入相关模块
(2)导入数据
(3)自定义函数
(4)调用函数
(5)模型预测
6、使用python中的模块实现决策树
(1)导入相关模块
(2)导入数据
(3)计算模型得分
(4)测试集预测并计算混淆矩阵
(5)计算模型评价指标
(6)绘制ROC曲线
1、如何构建决策树?
主要步骤如下:
(1)选择最优特征(构建根节点):决策树是依靠信息熵变化的程度来选择最优特征的,并以此分割训练数据集;
(2)生成决策树(叶子节点的选择):若子集被基本正确分类,构建叶结点,否则,继续选择新的最优特征;重复上面两步,直到所有训练数据子集被正确分类;决策树的三种常见算法,则是根据选择最优属性时计算的信息熵函数不同划分的。ID3 是根据信息熵,C4.5是根据信息增益率。CART是采用了基尼Gini系数。
(3)剪枝(防止过拟合):剪枝是把通过训练集得到的决策树,切掉一些叶子节点,一方面可以减少判决步骤,提高判决效率。但更主要的是,防决策树模型对训练集数据过拟合,使决策树具有更好的泛化能力。
2、特征选择
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。经验上人叼这样的特征对决策树学习的精度影响不大。通常特征选择的准则是信息增益和信息增益比,特征选择是决定用哪个特征来划分特征空间。
3、决策树生成
4、决策树剪枝
优秀的决策树是:在具有好的拟合和泛化能力的同时,深度小、叶结点少。所以为了更好的契合真实情况,需要对决策树进行剪枝操作。一般情况下有两种剪枝方法:
预剪枝:在构造决策树的过程中,先对每个结点在划分前进行估计,如果当前结点的划分不能提高泛化能力,则停止划分,将当前结点标记为叶结点。
后剪枝:生成一颗完整的决策树之后,自底向上地对内部结点进行考察,若此内部结点变为叶结点,可以提升泛化性能,则做此替换。
总结:预剪枝 ----> 边构造边剪枝,后剪枝 ----> 构造完再剪枝
5、实现决策树案例1—自定义函数
(1)导入相关模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inlinefrom sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
import math
from math import log
import pprint
(2)导入数据
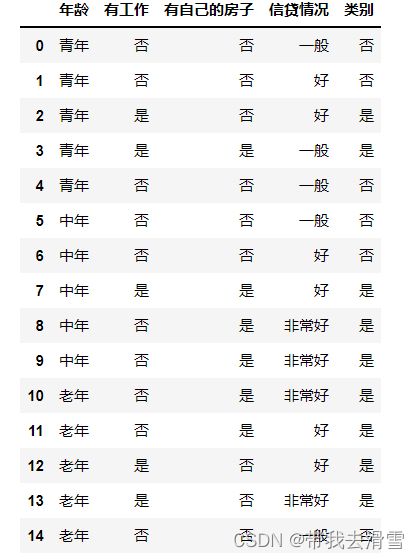
def create_data():
datasets = [['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
# 返回数据集和每个维度的名称
return datasets, labelsdatasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
train_data输出结果:
(3)自定义函数
class Node:
def __init__(self, root=True, label=None, feature_name=None, feature=None):
self.root = root
self.label = label
self.feature_name = feature_name
self.feature = feature
self.tree = {}
self.result = {
'label:': self.label,
'feature': self.feature,
'tree': self.tree
}def __repr__(self):
return '{}'.format(self.result)def add_node(self, val, node):
self.tree[val] = nodedef predict(self, features):
if self.root is True:
return self.label
return self.tree[features[self.feature]].predict(features)
class DTree:
def __init__(self, epsilon=0.1):
self.epsilon = epsilon
self._tree = {}# 熵
@staticmethod
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p / data_length) * log(p / data_length, 2)
for p in label_count.values()])
return ent# 经验条件熵
def cond_ent(self, datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
for p in feature_sets.values()])
return cond_ent# 信息增益
@staticmethod
def info_gain(ent, cond_ent):
return ent - cond_entdef info_gain_train(self, datasets):
count = len(datasets[0]) - 1
ent = self.calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return best_def train(self, train_data):
"""
input:数据集D(DataFrame格式),特征集A,阈值eta
output:决策树T
"""
_, y_train, features = train_data.iloc[:, :
-1], train_data.iloc[:,
-1], train_data.columns[:
-1]
# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回T
if len(y_train.value_counts()) == 1:
return Node(root=True, label=y_train.iloc[0])# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回T
if len(features) == 0:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
max_feature_name = features[max_feature]# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回T
if max_info_gain < self.epsilon:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])# 5,构建Ag子集
node_tree = Node(
root=False, feature_name=max_feature_name, feature=max_feature)feature_list = train_data[max_feature_name].value_counts().index
for f in feature_list:
sub_train_df = train_data.loc[train_data[max_feature_name] ==
f].drop([max_feature_name], axis=1)# 6, 递归生成树
sub_tree = self.train(sub_train_df)
node_tree.add_node(f, sub_tree)# pprint.pprint(node_tree.tree)
return node_treedef fit(self, train_data):
self._tree = self.train(train_data)
return self._treedef predict(self, X_test):
return self._tree.predict(X_test)
(4)调用函数
datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(train_data)
tree输出结果:
{'label:': None, 'feature': 2, 'tree': {'否': {'label:': None, 'feature': 1, 'tree': {'否': {'label:': '否', 'feature': None, 'tree': {}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}
(5)模型预测
dt.predict(['老年', '否', '否', '一般'])
输出结果:
'否'
6、使用python中的模块实现决策树
(1)导入相关模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inlinefrom sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import cohen_kappa_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
(2)导入数据
data=pd.read_csv("E:\工作\硕士\博客\博客44-/车辆保险训练集.csv")
X_raw=data.iloc[:,:-1]
X = pd.get_dummies(X_raw)
y=data.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.2, random_state=100)
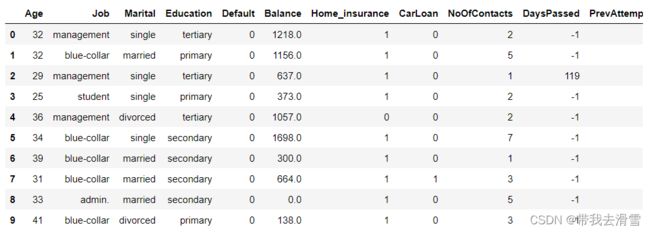
data.info()
data.head(10)部分输出结果:
(3)计算模型得分
clf = DecisionTreeClassifier(criterion='gini',max_depth=6, max_features=6,random_state=123)
model=clf.fit(X_train, y_train)
clf.score(X_test, y_test)输出结果:
0.8025
(4)测试集预测并计算混淆矩阵
y_pred_clf = clf.predict_proba(X_test)
y_pred_clf[:5]pred = model.predict(X_test)
pred[:5]输出结果:
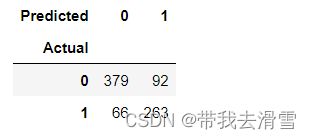
array([0, 0, 0, 1, 0], dtype=int64)table = pd.crosstab(y_test, pred, rownames=['Actual'], colnames=['Predicted'])
table输出结果:
(5)计算模型评价指标
from sklearn import metrics
print("树模型在测试集上的准确度为:", metrics.accuracy_score(pred, y_test))
print("树模型在测试集上的精度为:", metrics.average_precision_score(pred, y_test))
print("树模型在测试集上的召回率为:", metrics.recall_score(pred, y_test))
print("树模型在测试集上的F1度量为:", metrics.f1_score(pred, y_test))
metrics.plot_confusion_matrix(clf, X_test, y_test)
plt.show()输出结果:
树模型在测试集上的准确度为: 0.8025 树模型在测试集上的精度为: 0.7072256945930905 树模型在测试集上的召回率为: 0.7408450704225352 树模型在测试集上的F1度量为: 0.7690058479532164
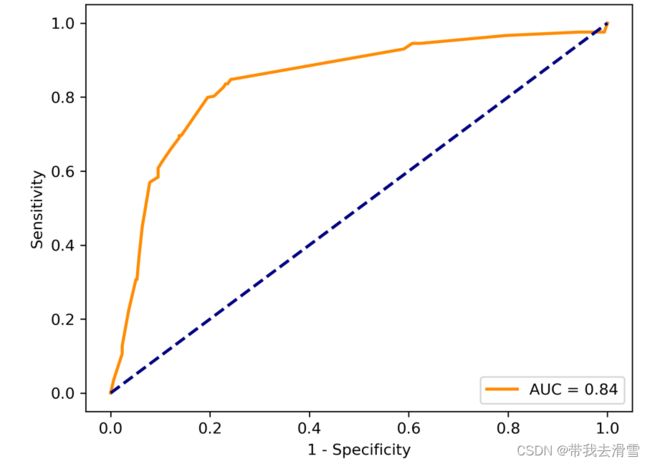
(6)绘制ROC曲线
import sklearn.metrics as metrics
y_pred_clf = clf.predict_proba(X_test)[:,1]
fpr, tpr, threshold=metrics.roc_curve(y_test,y_pred_clf)
roc_auc = metrics.auc(fpr, tpr)
#plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % roc_auc)#生成ROC曲线
lw = 2
plt.plot(fpr, tpr, color='darkorange',lw=lw, label='AUC = %0.2f' % roc_auc) ###假正率为横坐标,真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('1 - Specificity')
plt.ylabel('Sensitivity')
# plt.title('ROCs for Densenet')
plt.legend(loc="lower right")plt.savefig("E:\工作\硕士\博客\博客44-/squares1.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:https://pan.baidu.com/s/1E59qYZuGhwlrx6gn4JJZTg?pwd=2138
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!