【动手学深度学习】--03.多层感知机MLP

多层感知机

1.原理

官方笔记：多层感知机

1.1感知机

训练感知机

收敛定理

问题：感知机不能拟合XOR问题，它只能产生线性分割面

总结：

• 感知机是一个二分类模型，是最早的AI模型之一
• 它的求解算法等价于使用批量大小为1的梯度下降
• 它不能拟合XOR函数，导致的第一次AI寒冬

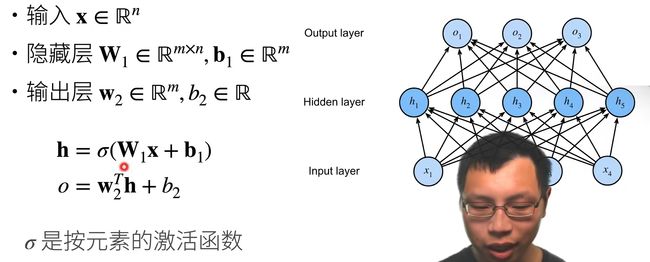
1.2多层感知机MLP

单隐藏层

1.3激活函数

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。 由于激活函数是深度学习的基础，下面简要介绍一些常见的激活函数。

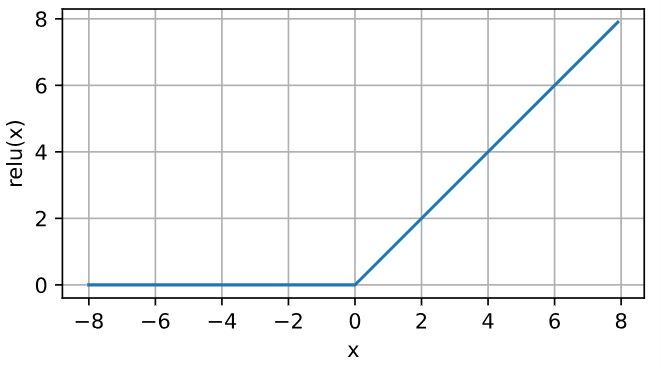
ReLU激活函数

Sigmoid函数

tanh函数

总结：

• 多层感知机使用隐藏层和激活函数来得到非线性模型
• 常用激活函数是Sigmoid、Tanh、ReLU
• 使用Softmax来处理多分类
• 超参数为隐藏层数，和各个隐藏层大小

2.从零开始实现多层感知机

继续使用Fashion-MNIST图像分类数据集

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2.1初始化模型参数

回想一下，Fashion-MNIST中的每个图像由28×28=784个灰度像素值组成。 所有图像共分为10个类别。 忽略像素之间的空间结构， 我们可以将每个图像视为具有784个输入特征 和10个类的简单分类数据集。 首先，我们将实现一个具有单隐藏层的多层感知机， 它包含256个隐藏单元。 注意，我们可以将这两个变量都视为超参数。通常，我们选择2的若干次幂作为层的宽度。 因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。注意，对于每一层我们都要记录一个权重矩阵和一个偏置向量

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

这里对权重系数W1，W2进行最后的乘0.01运算，是因为randn默认从（mean（均值） = 0, std（方差） = 1）的正态分布随机取值，乘0.01可以使方差变小，取值更稳定平滑

能不能把W和b的值都设置为0？ ——>显然不行，此时梯度消失，就没法根据反向传播来更新参数的大小从而学习

2.2激活函数

torch.zeros_like() ：生成和括号内变量维度维度一致的全是零的tensor。

def relu(x):
    a = torch.zeros_like(X)
    return torch.max(X,a)

2.3 模型

因为我们忽略了空间结构， 所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。

def net(X):
    X = X.reshape((-1,num_inputs))
    H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

2.4损失函数

loss = nn.CrossEntropyLoss(reduction='none')

这里损失函数必须加入reduction = ‘none’，可以保留每轮损失函数的梯度，才可以让我们最后画图

2.5训练

num_epochs,lr = 10,0.1
updater = torch.optim.SGD(params,lr = lr)
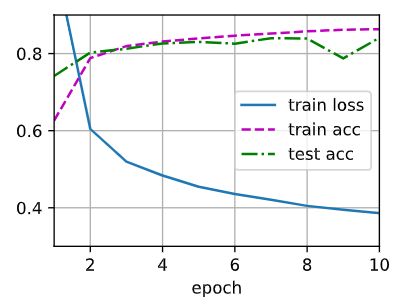
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,updater)

d2l.predict_ch3(net, test_iter)

3.多层感知机的简洁实现

3.1模型

添加了2个全连接层（之前我们只添加了1个全连接层）。 第一层是隐藏层，它包含256个隐藏单元，并使用了ReLU激活函数。 第二层是输出

nn.Flattern()函数详解

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

不需要自己定义平滑层以及定义ReLU激活函数

3.2训练

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
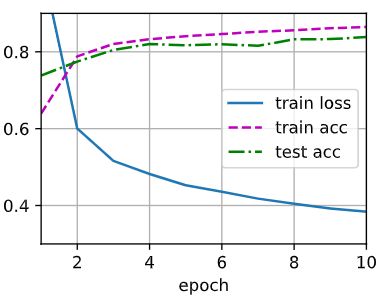
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)