强化学习中Ornstein-Uhlenbeck噪声什么使用最合理以及效果如何
读过 DDPG 论文 [1] 的同学几乎都会有一个问题,论文中使用 Ornstein-Uhlenbeck 噪声用于探索,比较难理解,参数又多,真的会比简单的高斯噪声等更有效吗?
由于大部分回答都没有说清楚甚至**完全相反地解释**该部分,本文会尝试从噪声在强化学习中的应用背景、Ornstein-Uhlenbeck 过程的定义、产生作用的原因、实验四部分阐述原因。
先放结论:相比于独立噪声,OU 噪声适合于惯性系统,尤其是时间离散化粒度较小的情况,此外,它可以保护实际系统,如机械臂。之所以大家觉得 OU 噪声没用,是因为强化学习 benchmark 都是仿真任务,而且往往都不用考虑时间离散化的问题。另外,即使遇到时间离散粒度小的问题,一般直接增大离散化粒度之后独立噪声也可以起到很好的效果。
1.DDPG 中的探索噪声
我们知道,DDPG 是典型的 off-policy 的方法,可叠加噪声的执行策略会独立于评估 / 学习的策略。也就是说,DDPG 学习的策略是确定性策略,即确定性的 Actor 网络,而探索部分可以自定义探索噪声。
先不考虑文中的 OU 噪声,一提到噪声,首先想到的是简单又易于实现的高斯噪声。并且,确定性策略加上高斯噪声后,形式上就和 REINFORCE 等 Actor-Critic 的随机策略一致了。
(1)高斯噪声
策略网络直接的输出,作为均值,叠加上高斯分布 ϵ ∼ N ( 0 , σ 2 ) \epsilon\sim{N(0, \sigma^{2})} ϵ∼N(0,σ2) 即可。此时执行策略实际上就成了 π θ ( s t ) + ϵ ∼ N ( π θ ( s t ) , σ 2 ) \pi_{\theta}(s_t){+}\epsilon\sim{N(\pi_{\theta}(s_t), \sigma^{2})} πθ(st)+ϵ∼N(πθ(st),σ2) 。有需要的话,还可以进行截断。
action= agent.get_action(state) # 策略网络直接输出
action = action + np.clip(np.random.normal(0, sigma), -c, c) # 截断
显然,高斯噪声是时序上不相关的,前一步和后一步选取动作的时候噪声都是独立的。前后两动作之间也只是通过状态使其独立。
其实 TD3 算法 [2] 中正是采用这种探索噪声,他们声称:
Unlike the original implementation of DDPG, we used uncorrelated noise for exploration as we found noise drawn from the Ornstein-Uhlenbeck (Uhlenbeck & Ornstein, 1930) process offered no performance benefits.
真的是这样吗?
(2)Ornstein-Uhlenbeck 噪声
DDPG 中对引入 OU 噪声的说明如下图,即利用 OU 过程产生时序相关的探索,以提高在**惯性系统中的控制任务的探索效率。这里的惯性系统是指的环境。**
另外一处,同样提到 OU 噪声是为了在**有 momentum 的环境**中探索得更好。
先不谈控制理论,这个环境大概怎么理解呢?你可以想象为一个慢响应的环境,比如夏天在一个闷热的房间,你打开空调制冷 10 秒钟,温度不会马上降下来,维持它原来的状态,还是很热。再比如说,控制一辆高速行驶的卡车,你踩一脚刹车,车子不会立马停下来。Deepmind 说,这种情况下用 OU noise 比较好。
为什么?先来看看定义。
2. 什么是 Ornstein-Uhlenbeck 过程
OU 过程是一种随机过程,微分方程 [3] 如下,形式上很简单。其连续形式为
d x t = − θ ( x t − μ ) d t + σ d W t (1) dx_t=-\theta{(x_t-\mu)}dt+\sigma{dW_t}\tag{1} dxt=−θ(xt−μ)dt+σdWt(1)
其中是 μ \mu μ\mu 均值, θ \theta θ\theta 和 σ \sigma σ\sigma 都大于 0, W t W_t WtW_t 是维纳过程(布朗运动)。 x x xx 是状态,常见 1 维标量。
右边第二项是扰动,暂不考虑。其离散形式为
x ( t + Δ t ) − x ( t ) = − θ ( x ( t ) − μ ) Δ t (2) x(t+\Delta{t})-x(t)=-\theta{(x(t)-\mu)}\Delta{t}\tag{2} x(t+Δt)−x(t)=−θ(x(t)−μ)Δt(2)
为什么说 OU 过程是均值回归?当 x t x_t xtx_t 比均值 μ \mu μ\mu 大的时候,下一步状态就会变小;反之,下一步状态会变大。也就是说,状态偏离的时候会被拉到靠近均值。
此外,不考虑维纳过程, 直接积分得到(3)式。
x t = μ + ( x 0 − μ ) e − θ t (3) x_t=\mu+(x_0-\mu)e^{-\theta{t}}\tag{3} xt=μ+(x0−μ)e−θt(3)
θ \theta θ\theta 的作用就很明确了,其值越大,向均值靠近的速度就越快。而且是指数倍的靠近。
再考虑扰动项,维纳过程,每一段时间间隔内的增量,是服从高斯分布的。
W ( t ) − W ( s ) ∼ N ( 0 , σ 2 ( t − s ) ) (4) W(t)-W(s)\sim{N(0,\sigma^{2}(t-s))}\tag{4} W(t)−W(s)∼N(0,σ2(t−s))(4)
σ 2 \sigma^{2} σ2\sigma^{2} 则是维纳过程的参数,表示方差。在 OU 过程中,它也决定扰动的放大倍数。
数学形式上,维纳过程是**高斯白噪声的积分**。
注意,和上面说的高斯噪声不一样,是**积分!也就是说,即使我们只考虑第二项维纳过程,得到的每一步的噪声会是从 0 时刻开始高斯噪声的累加**,建议自己画个图。
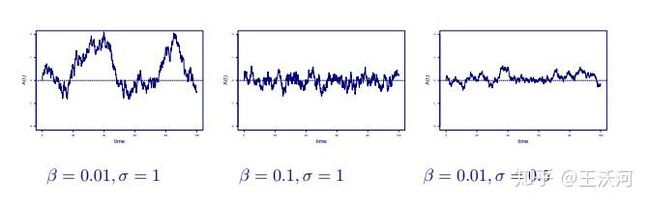
直观理解 θ σ \theta\space\sigma θ σ\theta\space\sigma 这两个参数的影响,一图胜千言,其中 β \beta β\beta 就是上面的 θ \theta θ\theta 。
代码很简单:
class OrnsteinUhlenbeckActionNoise:
def __init__(self, action_dim, mu = 0, theta = 0.15, sigma = 1):
self.action_dim = action_dim
self.mu = mu
self.theta = theta
self.sigma = sigma
self.X = np.ones(self.action_dim) * self.mu
def reset(self):
self.X = np.ones(self.action_dim) * self.mu
def sample(self):
dx = self.theta * (self.mu - self.X)
dx = dx + self.sigma * np.random.randn(len(self.X))
self.X = self.X + dx
return self.X
非常感谢
@pb 博
的指出,以上代码不完善,默认公式(2)OU 过程中
Δ t = 1 s \Delta{t}=1s Δt=1s\Delta{t}=1s
, 但实际上这里进行前向差分计算,
θ = 0.35 \theta=0.35 θ=0.35\theta=0.35
的时候,直接取采样时间 1s 可能相对于原始 OU 过程会有较大误差,刚看了下 OPENAI 的
baseline
,
Δ t \Delta{t} Δt\Delta{t}
设为参数,的默认值是 0.01s。
class OrnsteinUhlenbeckActionNoise(ActionNoise):
def __init__(self, mu, sigma, theta=.15, dt=1e-2, x0=None):
self.theta = theta
self.mu = mu
self.sigma = sigma
self.dt = dt
self.x0 = x0
self.reset()
def __call__(self):
x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)
self.x_prev = x
return x
def reset(self):
self.x_prev = self.x0 if self.x0 is not None else np.zeros_like(self.mu)
总结,作为强化学习的噪声,OU 噪声和高斯噪声相比,有什么区别?
由(2)式可以看到,OU noise 是自相关的,后一步的噪声受前一步的影响(且是马尔科夫的)。而第一部分阐述的高斯噪声,前后两步都是完全独立的。
所以,从图上看,OU noise 往往不会高斯噪声一样相邻的两步的值差别那么大,而是会绕着均值附近正向或负向探索一段距离,就像物价和利率的波动一样,这有利于在一个方向上探索。
参考 quora 的这个回答(强烈建议配合该回答食用):
Imagine trying to swim by nervously shaking your arms and legs in every direction in some chaotic and out of sync manner. That wouldn’t be very efficient, would it?
3. 什么时候可能有作用
两种情况:(1)惯性系统(环境)(2)保护实际机械臂 / 机器人
对于之前提到的惯性系统,为什么自相关的 OU 噪声会比高斯噪声更有作用呢?
回到之前的例子,现在 30°,学习控制空调温度到 26°,产生了一系列的不相关的在 0 均值附近高斯噪声,比如开 10 秒制热,再开 10 秒制冷,这样反复地在原地振荡,产生的作用就被平均了。而 OU 噪声,会往制冷方向多探索几步,这样积累的效果能探索到更低的温度。
quora 的这个回答从机器人控制的角度进行了解释:
DDPG is mainly used for continuous control tasks, such as locomotion. In this setting, the actions aa often correspond to exerting forces so as to move a physical body. Forces directly translate to accelerations, so they need to be integrated twice to affect the position xx of the system that we wish to control.
mx¨=amx¨=a
x=1m∫∫ax=1m∫∫a
Yet, the integration operator is a low-pass filter, which means that any high-frequency present in the action aa will be dampened.
简单来说,机器人中我们控制的是力,力作用到物体的速度或位移,这个动态过程(环境)是一个积分过程,积分过程正是常说的 “惯性系统”。
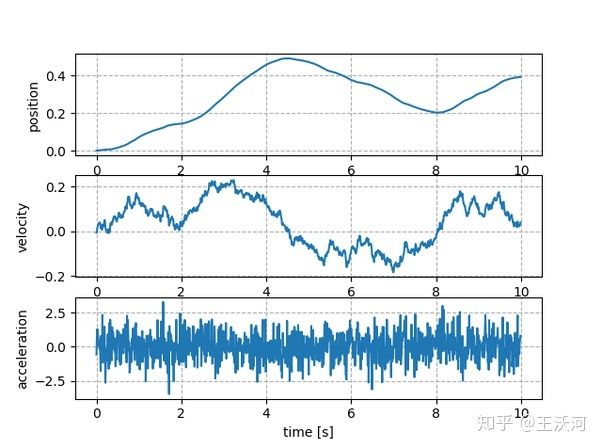
积分过程是典型的低通滤波,高斯噪声这种独立的噪声前后两步差别太大,会被过滤掉:
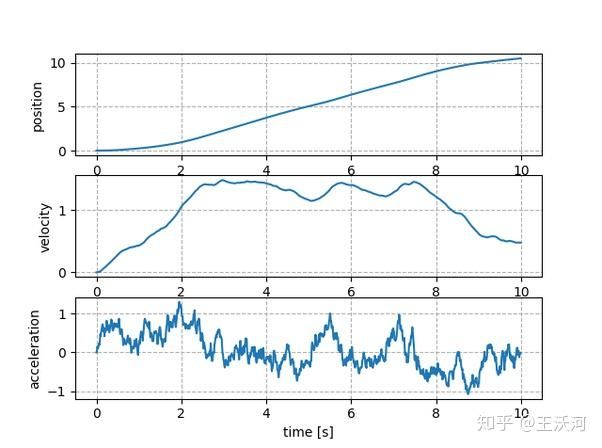
高斯噪声使得速度和位移的探索极为有限,而 OU 噪声由之前说的特点,则可以探索的更远:
DDPG 中引用的这篇文献 [4] 从另一方面探讨了关于机器人控制中引入自相关噪声的问题:
作者推导公式得出的结论是:
The finer time discretization, the less significant each particular action is, and the more noise it should contain. That leads to excessively discontinuous control signal, inappropriate for robotic applications.
如果使用独立的噪声,当时间离散的粒度越小,要维持同样的随机程度,则需要每一步噪声幅度(方差)就要越大,这就会导致前后两步相差极其的远,并不适合真实的机械臂。
文中声称,自相关的噪声能使得控制信号较为连续,可以在时间粒度小的时候,达到类似的效果,不过相比于采样时间大 + 独立噪声的方案,训练可能会慢些——其实也很好理解,采样时间较大的时候,即使是独立的噪声,动作带来的效果也很容易被验证,从而可以快速调整策略。而采样时间小的时候,自相关噪声走连续的几步才能得到验证,调整的周期也更长。
所以!不要再抱怨 OU 噪声没用了,只是你们不合适而已。你的环境可能不是惯性环境,即使是,也可能不用考虑离散时间的问题,即使离散时间小了,往往也可以增大离散时间的粒度解决。另外,大多数人不会将强化学习用于实际系统,也就跑跑仿真维持生活的样子(围笑)。
4. 实验
我们设计实验看看两种不同的探索噪声,在不同的离散化时间粒度(采样时间)下的表现。
任务:
设定值跟踪 (setpoints tracking) 任务,使得系统(环境)的输出达到预先设定的目标值。
环境是一阶系统(也是惯性系统),输入输出都是一维,传递函数如下:
G ( s ) = 10 2 s + 1 (5) G(s)=\frac{10}{2s+1}\tag{5} G(s)=2s+110(5)
方案:
DDPG 算法,训练时配合两种探索噪声,分别是高斯噪声和 Ornstein-Uhlenbeck 噪声。其中,高斯噪声 N ( 0 , 1 ) N(0,1) N(0,1)N(0,1) ,而 OU 过程参数 μ = 0 ; σ = 1 ; θ = 0.5 \mu=0;\sigma=1;\theta=0.5 μ=0;σ=1;θ=0.5\mu=0;\sigma=1;\theta=0.5 . 二者的 scale 基本一致。
状态、动作都是 1 维。奖赏可以认为就是绝对误差,即设定值减输出取绝对值后的相反数。
训练 140 回合,注意 reward 图中展示的是回报(一个回合内的累积奖赏)。
结果:
(1)采样时间 = 0.04s
我们可以看到,当采样时间较小的时候(0.04s),DDPG 采用 OU 噪声的结果是会比高斯噪声更好的。简便起见,我只展示一个 random seed 结果,线下换了 seed 结果类似。
(2)采样时间 = 0.1s
结果显示,当采样时间扩大到 0.1s 的时候,高斯噪声完全也可以完成任务,甚至训练到后期每个回合内的累积奖赏比 OU 噪声略微高一点点。这样就印证了之前的分析。
5. 结论
相比于独立噪声,OU 噪声适合于惯性系统,尤其是时间离散化粒度较小的情况,此外,它可以保护实际系统,如机械臂。之所以大家觉得 OU 噪声没用,是因为强化学习 benchmark 都是仿真任务,而且往往都不用考虑时间离散化的问题。另外,即使遇到时间离散粒度小的问题,一般直接增大离散化粒度之后独立噪声也可以起到很好的效果。
参考
- ^https://arxiv.org/abs/1509.02971
- ^https://arxiv.org/abs/1802.09477
- ^http://web.math.ku.dk/~susanne/StatDiff/Overheads1b
- ^http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.696.1149&rep=rep1&type=pdf