AVL树_旋转平衡化抽象逻辑分析
文章目录
- 一.AVL树的基本概念
-
- 1.AVL树的节点定义
- 2.平衡因子与AVL树的定义
- 二.AVL树的节点插入与平衡化算法
-
- 1.节点的插入与平衡因子的调整
-
- 平衡因子调整算法
- 插入新节点后的最小失衡子结构
- 2.最小失衡子结构的旋转平衡化
-
- 最小失衡子结构抽象化
- 旋转平衡化情形(1)
- 旋转平衡化情形(2)
- 旋转平衡化情形(3)
- 旋转平衡化情形(4)
- 三.AVL类代码托管
G. M. Adelson-Velsky和E. M. Landis两位数学家在1962年发明了自平衡二叉搜索树,计算机科学界从此进入了数据高速存储和检索的时代。
一.AVL树的基本概念
1.AVL树的节点定义
template<class KEY, class VALUE>
struct AVLTreeNode
{
AVLTreeNode<KEY, VALUE>* _pleft;
AVLTreeNode<KEY, VALUE>* _pright;
AVLTreeNode<KEY, VALUE>* _pParent; //前驱指针
//key_value键值对(KEY用于搜索,VALUE用于存储数据)
pair<KEY, VALUE> _key_value;
//以该节点为根节点的子树的平衡因子
int _balanceFactor;
//结点构造函数
AVLTreeNode(const pair<KEY, VALUE>& pairdata)
: _pleft(nullptr),
_pright(nullptr),
_pParent(nullptr),
_key_value(pairdata),
_balanceFactor(0)
{}
};
- 相比于二叉搜索树,AVL树的节点定义中新增了用于记录左右子树高度差的平衡因子,同时为了方便后续的算法实现,增加了节点前驱指针方便回溯。
2.平衡因子与AVL树的定义
- AVL树中每个节点都有一个平衡因子,节点的平衡因子等于该节点的右子树的高度减去左子树的高度(即记录了左右子树的高度差),AVL树的定义:
- AVL树满足二叉搜索树的所有性质
- AVL树根节点的平衡因子的绝对值小于或等于一
- AVL树的左右子树也是AVL树
- AVL树满足递归定义.根据AVL树的定义,树中所有节点的平衡因子的绝对值都不超过1,而且具有N个节点的AVL树的高度的数量级为(严格)logN
二.AVL树的节点插入与平衡化算法
AVL树的节点插入算法在二叉搜索树的节点插入算法的基础上增加了平衡因子的更新与平衡化的操作
1.节点的插入与平衡因子的调整
- 第一步先按照二叉搜索树的节点插入方式插入新节点:
//插入节点并更新树的平衡因子,并判断是否要执行旋转
bool insert(const Pair& KEYVALUE)
{
if (_root == nullptr)
{
_root = new Node(KEYVALUE);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
//查找插入的位置
while (cur != nullptr)
{
if (cur->_key_value.first < KEYVALUE.first)
{
parent = cur;
cur = cur->_pright;
}
else if (cur->_key_value.first > KEYVALUE.first)
{
parent = cur;
cur = cur->_pleft;
}
else
{
//KEY值重复,无法插入
return false;
}
}
//找到空位置执行插入
cur = new Node(KEYVALUE);
if (parent->_key_value.first < KEYVALUE.first)
{
//向右孩子插入
parent->_pright = cur;
cur->_pParent = parent;
}
else
{
parent->_pleft = cur;
cur->_pParent = parent;
}
}
- 插入节点后树的高度可能会发生变化,因此需要更新平衡因子
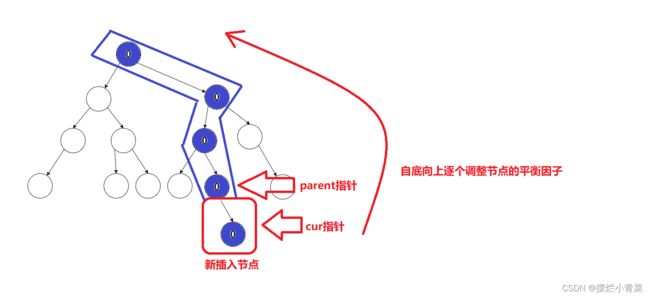
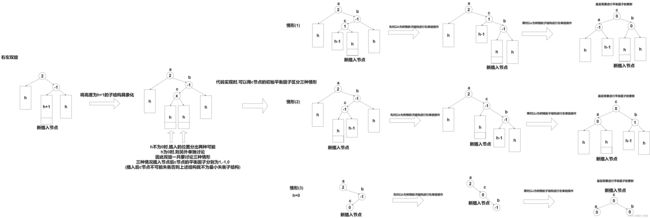
- 二叉搜索树节点插入算法会将新节点插入到搜索树的某个叶子节点的位置,插入新节点后,只有新节点到树的根节点的连通路径上(根据树的定义,该条连通路径是唯一的)的节点的平衡因子可能会改变(这一点十分重要),比如:
- 因此插入节点后我们只需从新插入节点的父节点开始自底向上调整连通路径上的节点的平衡因子即可.
平衡因子调整算法
- parent节点的平衡因子发生变化后,根据AVL树的性质,调整循环中一共要分出三种情况进行讨论:
- 调整后parent的平衡因子为0 (0只能由1(或者-1)减一(或加一)得来,说明以parent为根的子结构的高度不变),此后无需再继续向上调整平衡因子
- 调整后parent的平衡因子为1或者-1 (说明插入节点后以parent为根的子结构的高度发生了变化),需要继续向上调整平衡因子
- 调整后parent的平衡因子为2或者-2 (说明子结构失衡,接下来需要平衡化算法进行处理)
- 注意按照AVL树的数据结构,插入新节点后不可能出现某个节点的平衡因子绝对值大于2的情况(否则说明数据结构不符合AVL树的定义)
- 平衡因子的调整循环:
//插入的节点在叶子位置,只有该叶子节点所在的连通路径上的节点的平衡因此会受影响
//完成节点插入后更新平衡因子(沿着连通路径自底向上向上更新平衡因子)
while (parent)
{
if (parent->_pright == cur)
{
//右子树高度加一,平衡因子加一
parent->_balanceFactor++;
}
else
{
//左子树高度加一,平衡因子减一
parent->_balanceFactor--;
}
//根据调整后parent的平衡因子,判断是否需要旋转或继续回溯调整祖先的平衡因子
//parent的平衡因子变为0说明左右子树在插入节点后高度相同,则子树的高度没有变化,无须再回溯调整
if (parent->_balanceFactor == 0)
{
break;
}
//parent的平衡因子变为1或-1说明原来parent的平衡因子为0,此时树的高度增加了1,需要继续向上调整祖先的平衡因子
//[以前驱节点为树根的子树的平衡因子受当前子树的高度的影响(呈递推关系)]
else if (parent->_balanceFactor == -1
|| parent->_balanceFactor == 1)
{
cur = parent;
parent = parent->_pParent;
}
//parent的平衡因子变为2或-2,插入节点后子树失衡,需要平衡化处理
else if (parent->_balanceFactor == -2
|| parent->_balanceFactor == 2)
{
//平衡化算法
}
//AVL树出现不合法情况,报错终止程序(AVL树插入节点后不可能出现平衡因子大于2的结点)
else
{
assert(false);
return false;
}
}
插入新节点后的最小失衡子结构
- AVL树插入新节点后,在连通路径上调整节点的平衡因子的过程中,可能会出现某个节点的平衡因子变为2或-2的情况,我们将连通路径上自底向上第一个平衡因子变为2或-2的节点称为高度最大的失衡节点
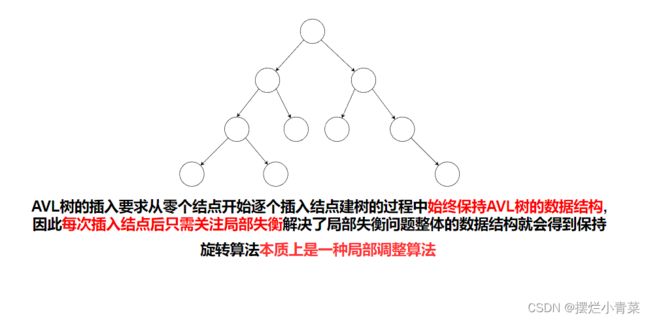
- 以高度最大的失衡节点为树根的子结构称为最小失衡子结构(易知,插入新节点前最小失衡子结构至少有两个节点),比如:
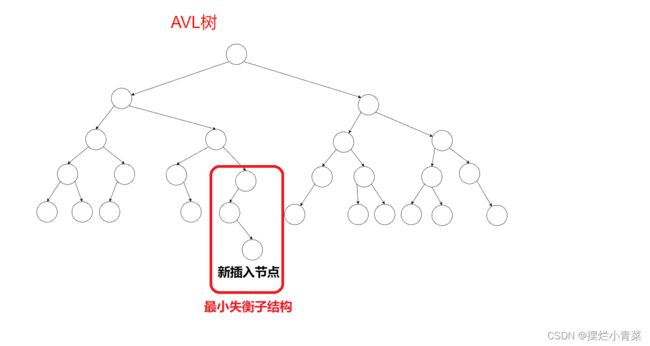
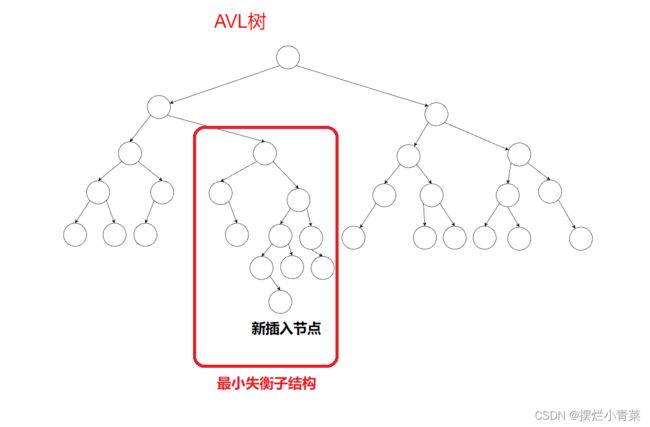
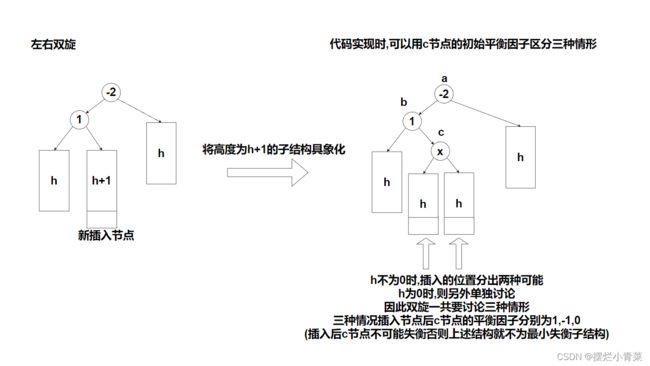
- 进一步思考:如果将最小失衡子结构平衡化并且将其整体高度减小1,则整个数据结构就会恢复为AVL树
- 因此所谓的旋转平衡化实质上是一种局部调整算法,实质上是对最小失衡子结构进行平衡化的算法.
2.最小失衡子结构的旋转平衡化
最小失衡子结构抽象化
-
针对最小失衡子结构设计平衡化算法之前,需要对最小失衡子结构进行抽象化分类(插入新节点前最小失衡子结构的节点数目大于或等于二个)
-
上图抽象结构中的方块表示高度为h的AVL子树(h>=0).
-
针对最小失衡子结构的抽象分类,平衡化算法需要根据四种不同的情形进行设计:
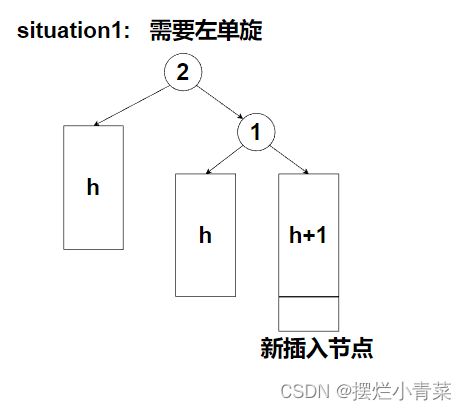
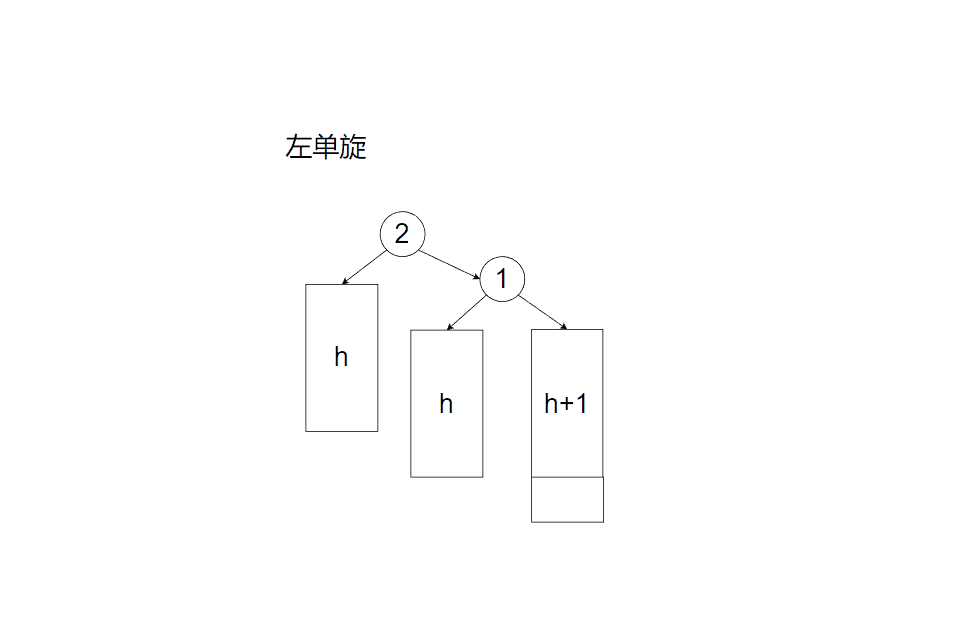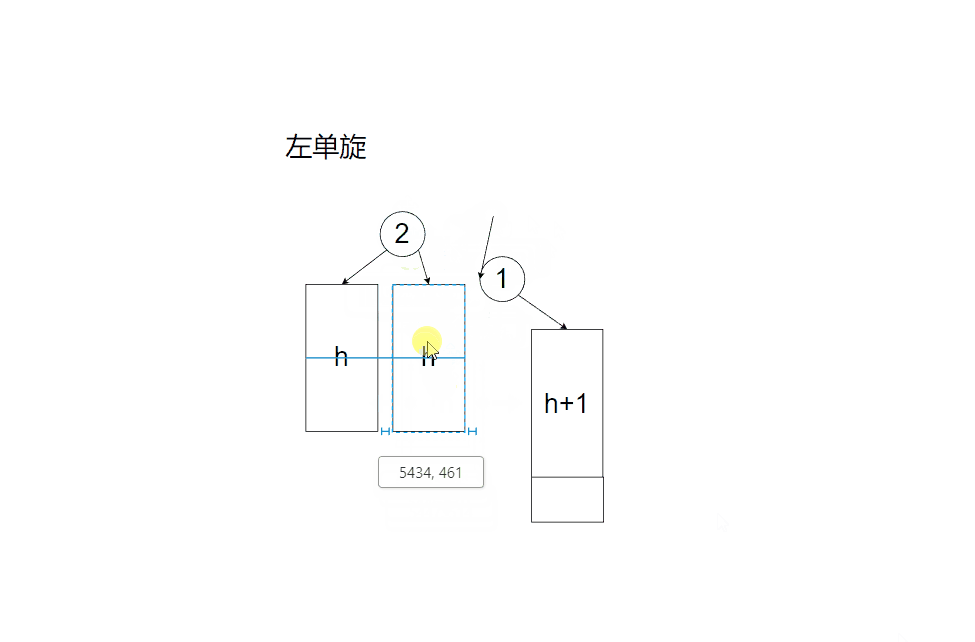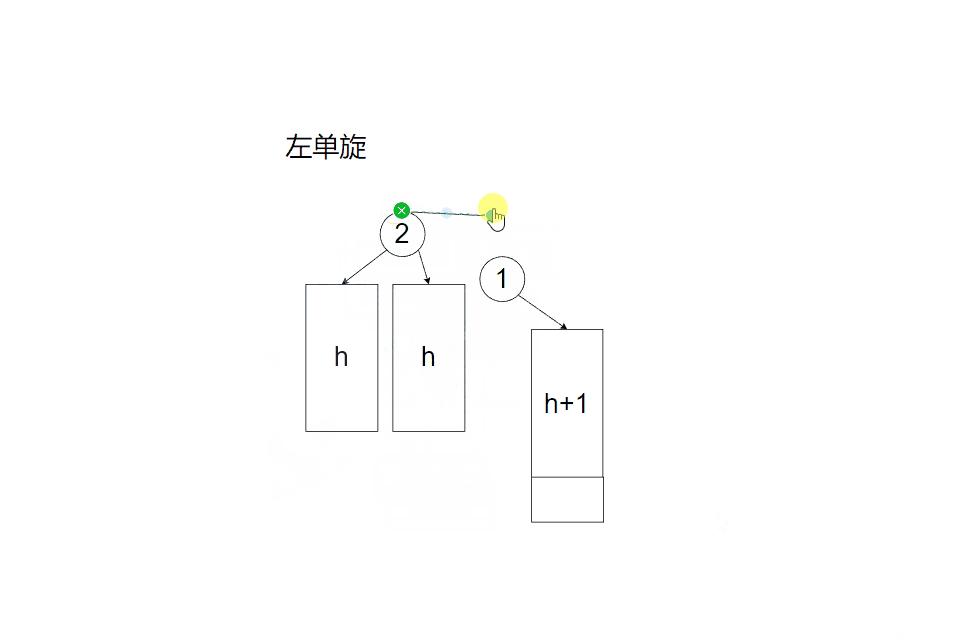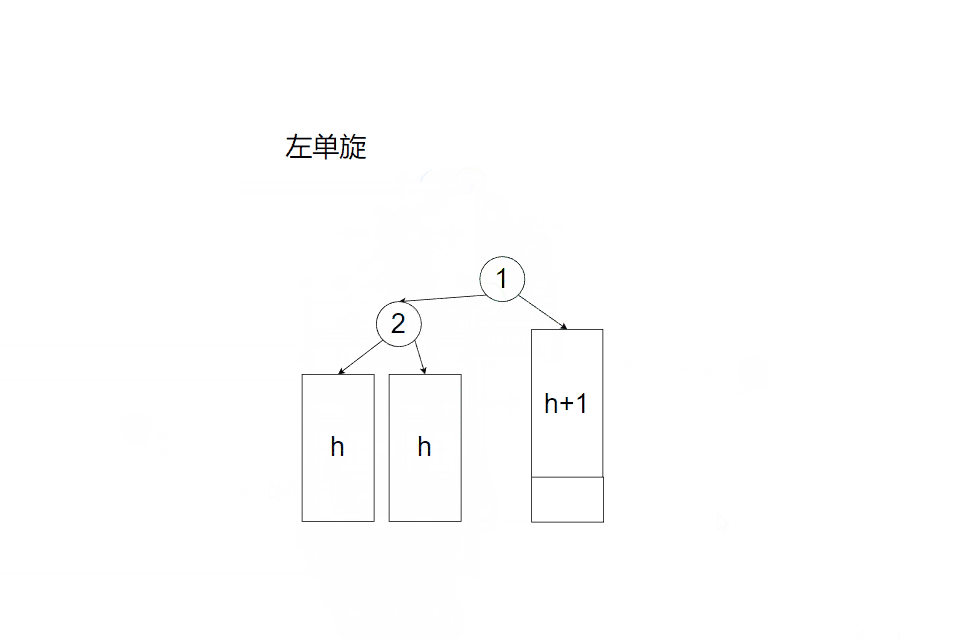
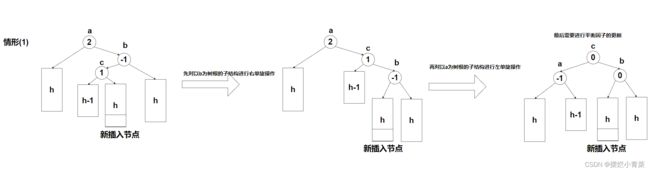
旋转平衡化情形(1)
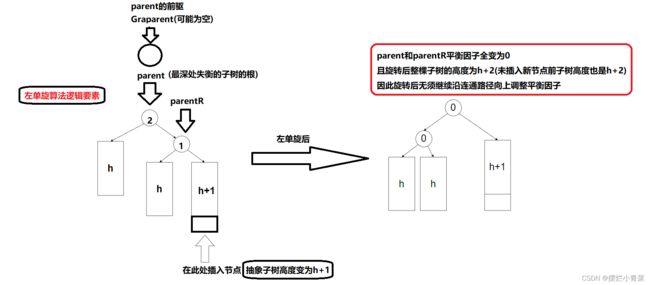
旋转平衡化情形(2)
- 左单旋和右单旋的接口实现:
//左单旋成员接口
void _RotationSL(Node* parent)
{
//整个子结构的祖先(可能为空,即parent就是整棵树的树根)
Node* Graparent = parent->_pParent;
Node* parentR = parent->_pright;
//parentR的左子树(可能为空)
Node* parentRLSon = parentR->_pleft;
//左单旋
parent->_pright = parentRLSon;
//注意parentLSon可能为空
if (parentRLSon)
{
parentRLSon->_pParent = parent;
}
parentR->_pleft = parent;
parent->_pParent = parentR;
//注意GGraparent可能为空
if (Graparent)
{
if (Graparent->_pleft == parent)
{
Graparent->_pleft = parentR;
}
else
{
Graparent->_pright = parentR;
}
}
else
{
_root = parentR;
}
parentR->_pParent = Graparent;
//调整平衡因子
parent->_balanceFactor = 0;
parentR->_balanceFactor = 0;
}
//右单旋成员接口
void _RotationSR(Node* parent)
{
Node* Graparent = parent->_pParent;
Node* parentL = parent->_pleft;
Node* parentLRSon = parentL->_pright;
//右单旋
parent->_pleft = parentLRSon;
if (parentLRSon)
{
parentLRSon->_pParent = parent;
}
parentL->_pright = parent;
parent->_pParent = parentL;
if (Graparent)
{
if (Graparent->_pleft == parent)
{
Graparent->_pleft = parentL;
}
else
{
Graparent->_pright = parentL;
}
}
else
{
_root = parentL;
}
parentL->_pParent = Graparent;
//更新平衡因子
parentL->_balanceFactor = 0;
parent->_balanceFactor = 0;
}
- 接下来的两种情形的失衡子结构需要用到双旋算法,双旋平衡化是通过两次单旋实现的
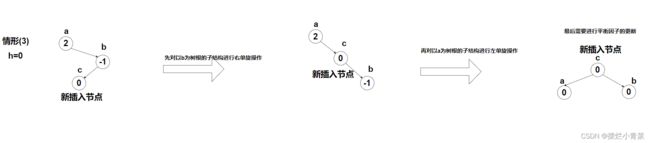
旋转平衡化情形(3)
- 右左双旋总体图解:
- 分块展示:
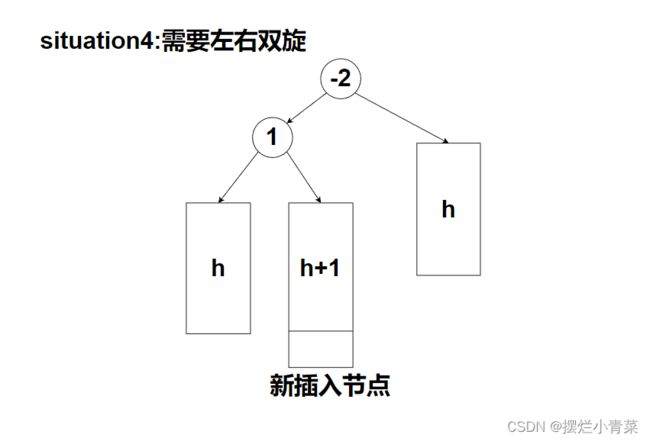
旋转平衡化情形(4)
-
左右双旋总体图解:
-
分块展示:
-
左单旋和右单旋的接口实现:通过复用单旋接口即可实现
//左右双旋接口
void _RotationDLR(Node* parent)
{
Node* parentL = parent->_pleft;
Node* parentLRSon = parentL->_pright;
int _balancefactorOfparentLRSon = parentLRSon->_balanceFactor;
//先执行左单旋操作
_RotationSL(parentL);
//再执行右单旋操作
_RotationSR(parent);
//完成单旋后分三种情形更新平衡因子(根据parentLRSon的双旋前的平衡因子可以区分三种情况)
parentLRSon->_balanceFactor = 0;
if (_balancefactorOfparentLRSon == 1)
{
parent->_balanceFactor = 0;
parentL->_balanceFactor = -1;
}
else if (_balancefactorOfparentLRSon == -1)
{
parent->_balanceFactor = 1;
parentL->_balanceFactor = 0;
}
else if (_balancefactorOfparentLRSon == 0)
{
parent->_balanceFactor = 0;
parentL->_balanceFactor = 0;
}
//出现其他情形则说明数据结构不合法
else
{
assert(false);
}
}
//右左双旋接口
void _RotationDRL(Node* parent)
{
Node* parentR = parent->_pright;
Node* parentRLSon = parentR->_pleft;
int balancefactorOfparentRLSon = parentRLSon->_balanceFactor;
//执行右单旋
_RotationSR(parentR);
//执行左单旋
_RotationSL(parent);
//更新平衡因子
parentRLSon->_balanceFactor = 0;
if (balancefactorOfparentRLSon == 1)
{
parent->_balanceFactor = -1;
parentR->_balanceFactor = 0;
}
else if (balancefactorOfparentRLSon == -1)
{
parent->_balanceFactor = 0;
parentR->_balanceFactor = 1;
}
else if (balancefactorOfparentRLSon == 0)
{
parent->_balanceFactor = 0;
parentR->_balanceFactor = 0;
}
else
{
assert(false);
}
}
- 旋转平衡化算法令最小失衡子结构恢复平衡的同时保持了其二叉搜索树的性质,而且最小失衡子结构经过旋转后整体的高度恢复到了插入新节点之前的高度,从而整棵树在旋转平衡化后恢复了AVL树的数据结构.
三.AVL类代码托管
#include 