拓扑序列及其排序
目录
- 一、拓扑序列及其排序的相关概念
-
- 拓扑序列的定义
- 拓扑序列的性质
- 出度、入度、度数
- 拓扑排序
- 二、拓扑序列及其排序的应用
-
- 有向图的拓扑序列
-
- 代码实现
一、拓扑序列及其排序的相关概念
拓扑序列的定义
拓扑序列是对一个
有向无环图(DAG)(也称为拓扑图)而言的,有向图的拓扑序列是其顶点的线性排序,使得对每条有向边(u,v),u在序列中出现在v之前。
例如下图:
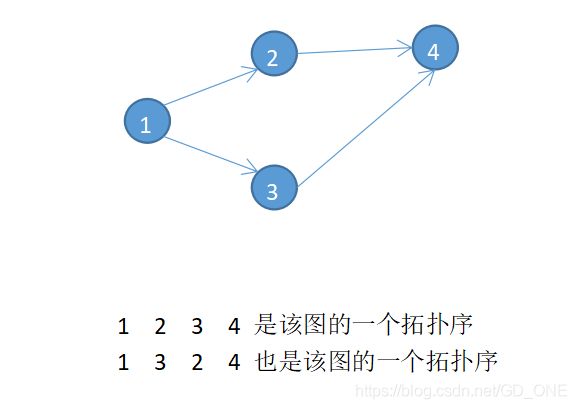
存在4条边:(1,3)(1,2)(2,4)(2,3)
该图的拓扑序列必须要满足以下两点:
- 每个顶点只出现一次。
- 对于图中的任何一条边,起点必须在终点之前。
拓扑序列的性质
- 对于一个有
n个顶点的DAG,可能存在多个不同的拓扑序列。 - 如果图中
存在环,则不能得到拓扑序列。如果图中不存在环,则至少存在一个拓扑序列。 - 可以使用广度优先搜索、深度优先搜索等图遍历算法求解拓扑序列。
- 拓扑序列在很多场景下有应用,比如为工程项目排序建立先后关系、计算程序中任务的执行顺序等。
- 拓扑序列可以用于检测图中是否存在环。如果可以成功生成拓扑序列,说明图中没有环,反之则说明有环。
- 对于一个DAG,可以根据拓扑序列将其转化为等价的序列图。
出度、入度、度数
出度(Out-degree):对于一个图中的某个顶点,出度表示从该顶点指向其他顶点的边的数量。它描述了从该顶点发散出去的连接数。
入度(In-degree):对于一个图中的某个顶点,入度表示指向该顶点的边的数量。它描述了进入该顶点的连接数。
度数(Degree):对于一个图中的某个顶点,度数等于其出度与入度的和。它描述了与该顶点相关的边的总数。
拓扑排序
①从图中选择一个入度为0的顶点,并输出该顶点;
②从图中删除该顶点及其相关联的有向边,调整被删除有向边的终点的入度(入度减1);
③重复①和②;
④直到所有顶点均被输出,拓扑序列完成;否则,无拓扑序列。
二、拓扑序列及其排序的应用
有向图的拓扑序列
题目描述:
给定一个 n n n 个点 m m m 条边的有向图,点的编号是 1 1 1 到 n n n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A A A 满足:对于图中的每条边 ( x , y ) (x,y) (x,y), x x x 在 A A A 中都出现在 y y y 之前,则称 A A A 是该图的一个拓扑序列。
输入格式:
第一行包含两个整数 n n n 和 m m m。
接下来 m 行,每行包含两个整数 x x x 和 y y y,表示存在一条从点 x x x 到点 y y y 的有向边 ( x , y ) (x,y) (x,y)。
输出格式:
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。否则输出−1。
数据范围:
1 ≤ n , m ≤ 1 0 5 1≤n,m≤10^5 1≤n,m≤105
输入样例:
3 3
1 2
2 3
1 3
输出样例:
1 2 3
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include
