二叉树及其遍历
文章目录
- 二叉树
-
- 树的定义
- 二叉树的定义
- 遍历
-
- 先序遍历
- 中序遍历
- 后序遍历
- 层次遍历
-
- 定义队列
- 层次创建二叉树
- 层次遍历
二叉树
树是一种非线性的数据结构,由若干个节点组成,节点之间存在一种父子关系,具有层次结构。二叉树是一种特殊的树结构,每个节点最多有两个子节点。树结构可以用来实现各种算法,例如二叉查找树、平衡二叉树、堆等。
树的定义
树(Tree) 是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:
- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可分为
m(m>0)个互不相交的有限集T1、T2、…、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
此外,树的定义还需要强调以下两点:
n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。m>0时,子树的个数没有限制,但它们一定是互不相交的。
二叉树的定义
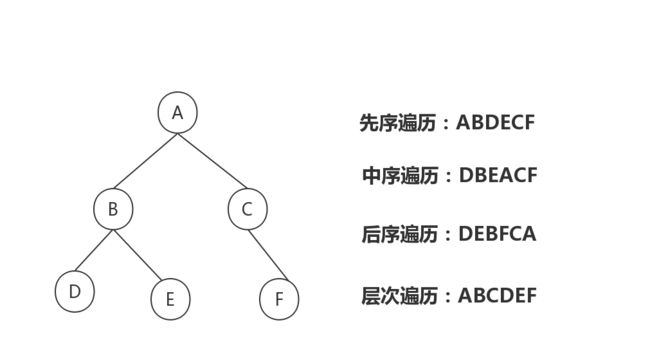
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
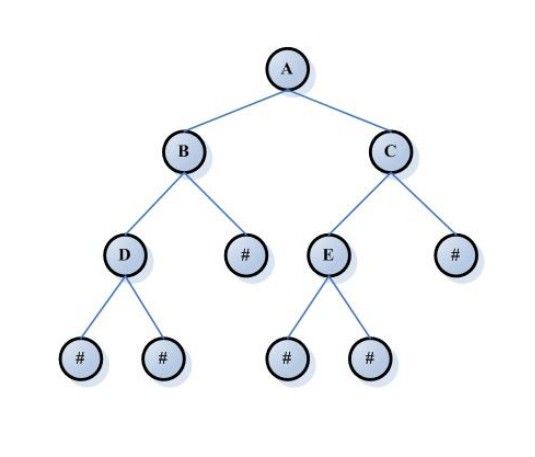
从定义和图例中可以看出,二叉树每个节点最多只会有两棵子树,且左右子树是有顺序的,次序不能随意颠倒。当一个节点既没有左子树也没有右子树,则该节点为叶子节点。
代码实现
结构体定义树
typedef struct Tree{
int val; //数据域
struct Tree *left; // 左子树
struct Tree *right; // 右子树
}Tree,*tree;
遍历
二叉树作为一种存储结构,将数据存入之后,则需要遍历对数据进行对应的处理。而二叉树的遍历分为四种:先(前)序遍历、中序遍历、后序遍历、层次遍历。
先序遍历
先序遍历是指从根节点开始,经过左子树,最后再遍历右子树,遍历顺序为:根节点->左子树->右子树。
代码实现
首先使用先序递归的创建一颗二叉树
// 创建新节点
Tree newNode(int val){
Tree root = (Tree) malloc(sizeof (tree));
root->val = val;
root->left = NULL;
root->right = NULL;
return root
}
Tree CreateBiTree(int* len){//创建一颗节点数为len的二叉树
if((*len)<=0){
return NULL;
}
int val; //创建一个数据接收参数。
printf("请输入插入数值:");
// 为根节点数据域赋值
scanf("%d",&val);
//创建一个根节点
Tree root = newNode(val);
(*len)--;
root->left = CreateBiTree(len); //递归创建左子树
root->right = CreateBiTree(len); //递归创建右子树
//创建完成后返回根节点
return root;
}
再进行先序遍历
//先序遍历
void preorder(Tree root){
if(root==NULL){
return ;
}
// 首先输出根节点的值
printf("节点的值:%d\n",root->val);
//先递归遍历左子树
preorder(root->left);
//递归遍历右子树
preorder(root->right);
}
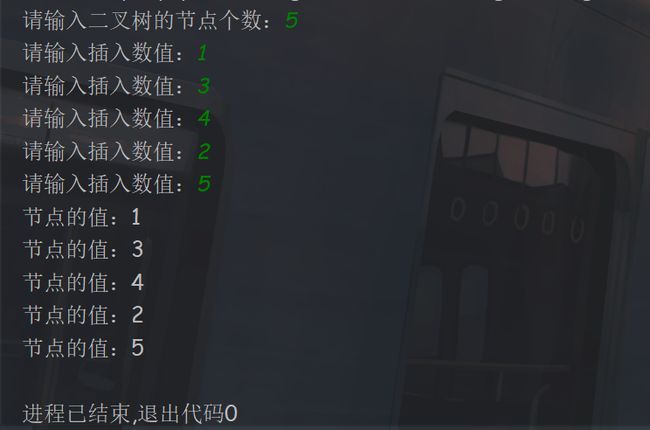
运行结果
中序遍历
中序遍历是指从左子树开始,再访问根节点,最后遍历右子树,遍历顺序为:左子树->根节点->右子树。
代码实现
利用先序递归创建一颗二叉树,并使用中序遍历二叉树
//中序遍历
void inorder(Tree root){
//如果节点为NULL,退出遍历
if(root==NULL){
return ;
}
//先递归遍历左子树
inorder(root->left);
// 输出根节点的值
printf("节点的值:%d\n",root->val);
//递归遍历右子树
inorder(root->right);
}
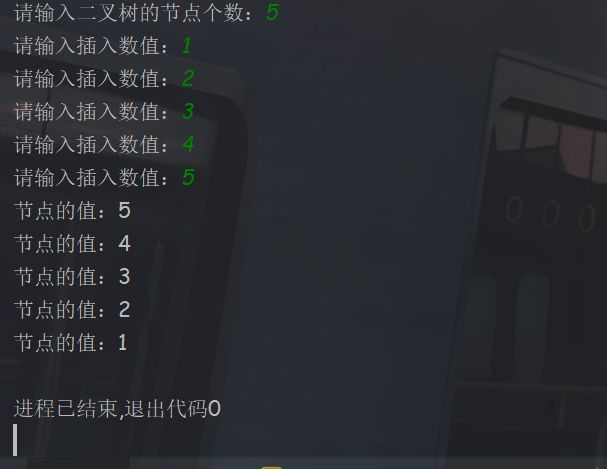
运行结果
后序遍历
后序遍历是指从左子树开始,再遍历右子树,最后访问根节点,遍历顺序为:左子树->右子树->根节点。
代码实现
// 后序遍历
void postorder(Tree root){
//如果节点为NULL,退出遍历
if(root==NULL){
return ;
}
//先递归遍历左子树
postorder(root->left);
//再递归遍历右子树
postorder(root->right);
//输出根节点的值
printf("节点的值:%d\n",root->val);
}
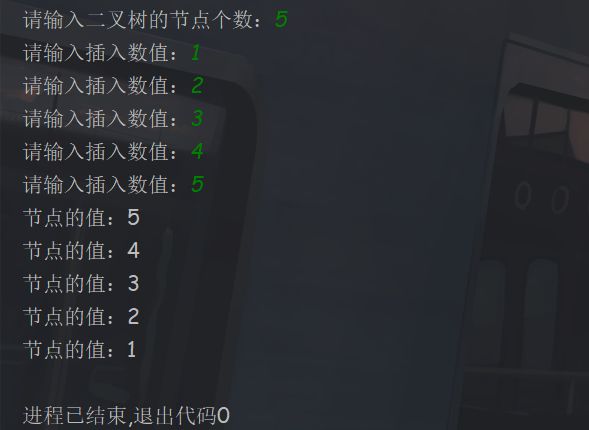
运行结果
为什么后序遍历和中序遍历的结果相同呢?
因为创建二叉树的时候使用的是前序递归,所以创建出来的二叉树都在根节点的左子树上,其右子树为空,此时这种情况被称为斜二叉树,并且也被称之为二叉树退化成单链表。这样创建出来的二叉树是很浪费空间且不规范的。
所以先序递归创建的二叉树是不可取的。此时就用到层次创建二叉树,层次创建是用到最多的创建方式,也是较为直观的一种创建方式。
层次遍历
层次遍历是指从根节点开始,然后一层一层向下遍历。
代码实现
一把是利用队列来实现层次创建及遍历二叉树
定义队列
// 定义队列
struct Queue {
struct Tree *Tree;
struct Queue *next;
};
// 初始化队列
void initQueue(struct Queue **head, struct Queue **tail) {
*head = *tail = NULL;
}
// 入队
void enQueue(struct Queue **head, struct Queue **tail, struct Tree *Tree) {
struct Queue *node = (struct Queue*)malloc(sizeof(struct Queue));
node->Tree = Tree;
node->next = NULL;
if (*head == NULL) {
*head = *tail = node;
} else {
(*tail)->next = node;
*tail = node;
}
}
// 出队
struct Tree* deQueue(struct Queue **head, struct Queue **tail) {
if (*head == NULL) {
return NULL;
}
struct Tree *Tree = (*head)->Tree;
if (*head == *tail) {
*head = *tail = NULL;
} else {
*head = (*head)->next;
}
return Tree;
}
层次创建二叉树
// 创建二叉树
struct Tree* createTree(int *arr, int size) { //arr为数据数组,size为层数
if (size == 0) {
return NULL;
}
// 创建根节点
struct Tree *root = (struct Tree*)malloc(sizeof(struct Tree));
root->val = arr[0];
root->left = NULL;
root->right = NULL;
// 初始化队列
struct Queue *head, *tail;
initQueue(&head, &tail);
enQueue(&head, &tail, root);
int i = 1;
// 层次遍历创建二叉树
while (i < size) {
struct Tree *node = deQueue(&head, &tail);
// 左子树
if (i < size && arr[i] != -1) { //当数据为-1时证明该处为空节点
node->left = (struct Tree*)malloc(sizeof(struct Tree));
node->left->val = arr[i];
node->left->left = NULL;
node->left->right = NULL;
enQueue(&head, &tail, node->left);
}
i++;
// 右子树
if (i < size && arr[i] != -1) {
node->right = (struct Tree*)malloc(sizeof(struct Tree));
node->right->val = arr[i];
node->right->left = NULL;
node->right->right = NULL;
enQueue(&head, &tail, node->right);
}
i++;
}
return root;
}
层次遍历
// 层次遍历
void levelOrder(struct Tree* root) {
if (root == NULL) {
return;
}
struct Queue *head, *tail; // 定义队头与队尾
initQueue(&head, &tail);
enQueue(&head, &tail, root);
while (head != NULL) {
struct Tree *node = deQueue(&head, &tail);
printf("%d ", node->val);
if (node->left != NULL) {
enQueue(&head, &tail, node->left);
}
if (node->right != NULL) {
enQueue(&head, &tail, node->right);
}
}
}
main函数
// 测试代码
int main() {
// 层次遍历序列,其中-1表示空节点
int arr[] = {1, 2, 3, 4, -1, -1, 5};
int size = sizeof(arr) / sizeof(int);
// 创建二叉树
struct Tree* root = createTree(arr, size);
// 打印二叉树
levelOrder(root);
return 0;
}
运行结果
层次遍历已经实现,接着使用层次创建二叉树,并实现先中后序遍历
运行结果分别为:
先序遍历
中序遍历
后序遍历