Lesson3-3:OpenCV图像处理---图像平滑
图像平滑
学习目标
- 了解图像中的噪声类型
- 了解平均滤波,高斯滤波,中值滤波等的内容
- 能够使用滤波器对图像进行处理
1 图像噪声
由于图像采集、处理、传输等过程不可避免的会受到噪声的污染,妨碍人们对图像理解及分析处理。常见的图像噪声有高斯噪声、椒盐噪声等。
1.1 椒盐噪声
椒盐噪声也称为脉冲噪声,是图像中经常见到的一种噪声,它是一种随机出现的白点或者黑点,可能是亮的区域有黑色像素或是在暗的区域有白色像素(或是两者皆有)。椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值,饱和的感应器导致像素值为最大值。
1.2 高斯噪声
高斯噪声是指噪声密度函数服从高斯分布的一类噪声。由于高斯噪声在空间和频域中数学上的易处理性,这种噪声(也称为正态噪声)模型经常被用于实践中。高斯随机变量z的概率密度函数由下式给出:
其中 z z z表示灰度值, μ μ μ表示 z z z的平均值或期望值, σ σ σ表示 z z z的标准差。标准差的平方 σ 2 {σ}^{2} σ2称为 z z z的方差。高斯函数的曲线如图所示。

2 图像平滑简介
图像平滑从信号处理的角度看就是去除其中的高频信息,保留低频信息。因此我们可以对图像实施低通滤波。低通滤波可以去除图像中的噪声,对图像进行平滑。
根据滤波器的不同可分为均值滤波,高斯滤波,中值滤波, 双边滤波。
2.1 均值滤波
采用均值滤波模板对图像噪声进行滤除。令 S x y S_{x y} Sxy 表示中心在 ( x , y ) (x, y) (x,y)点,尺寸为 m × n m×n m×n 的矩形子图像窗口的坐标组。 均值滤波器可表示为:
f ^ ( x , y ) = 1 m n ∑ ( s , t ) ∈ S x y g ( s , t ) \hat{f} (x,y) = \frac{1}{mn} \sum_{(s,t)∈S_{xy}}^{} g(s,t) f^(x,y)=mn1(s,t)∈Sxy∑g(s,t)
由一个归一化卷积框完成的。它只是用卷积框覆盖区域所有像素的平均值来代替中心元素。
例如, 3 x 3 3x3 3x3标准化的平均过滤器如下所示:
K = 1 / 9 [ 1 1 1 1 1 1 1 1 1 ] K=1/9 \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ \end{bmatrix} K=1/9 111111111
均值滤波的优点是算法简单,计算速度较快,缺点是在去噪的同时去除了很多细节部分,将图像变得模糊。
API:
cv.blur(src, ksize, anchor, borderType)
参数:
src:输入图像ksize:卷积核的大小anchor:默认值 ( − 1 , − 1 ) (-1,-1) (−1,−1) ,表示核中心borderType:边界类型
示例:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogsp.jpeg')
# 2 均值滤波
blur = cv.blur(img,(5,5))
# 3 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('均值滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
2.2 高斯滤波
二维高斯是构建高斯滤波器的基础,其概率分布函数如下所示:
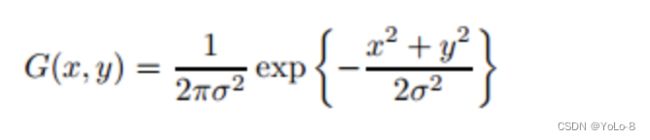
G ( x , y ) G(x,y) G(x,y)的分布是一个突起的帽子的形状。这里的 σ σ σ可以看作两个值,一个是 x x x方向的标准差 σ x σ_{x} σx ,另一个是 y y y方向的标准差 σ y σ_{y} σy。
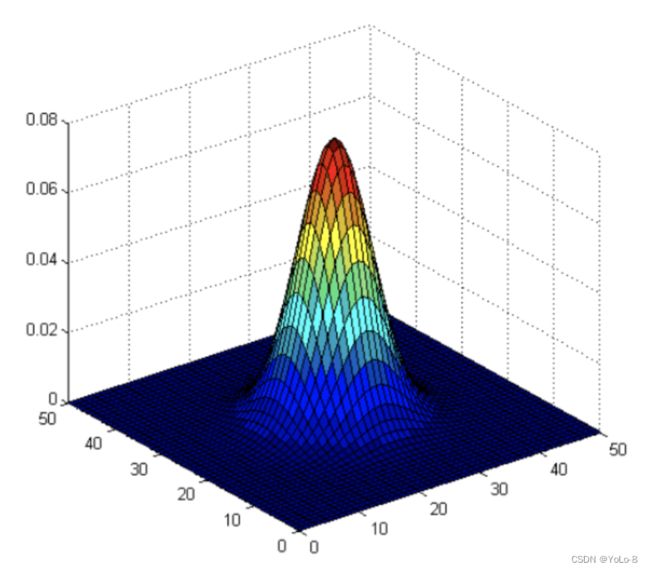
当 σ x σ_{x} σx 和 σ y σ_{y} σy取值越大,整个形状趋近于扁平;当 σ x σ_{x} σx 和 σ y σ_{y} σy取值越小整个形状越突起。
正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。计算平滑结果时,只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
高斯平滑在从图像中去除高斯噪声方面非常有效。
高斯平滑的流程:
为了计算权重矩阵,需要设定 σ σ σ的值。假定 σ = 1.5 σ=1.5 σ=1.5,则模糊半径为 1 1 1的权重矩阵如下:
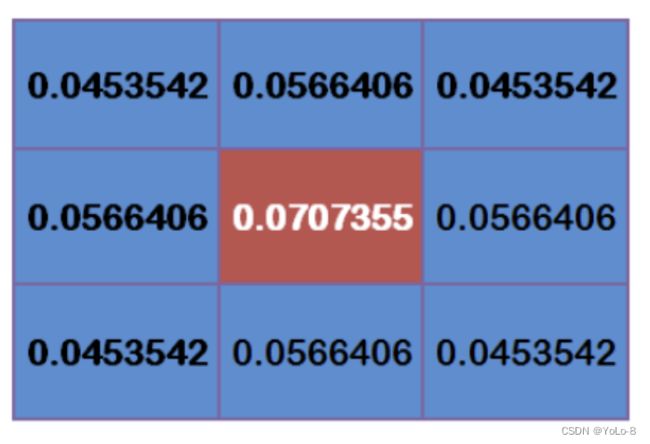
这 9 9 9个点的权重总和等于 0.4787147 0.4787147 0.4787147,如果只计算这 9 9 9个点的加权平均,还必须让它们的权重之和等于 1 1 1,因此上面 9 9 9个值还要分别除以 0.4787147 0.4787147 0.4787147,得到最终的权重矩阵。

- 计算高斯模糊
有了权重矩阵,就可以计算高斯模糊的值了。
假设现有 9 9 9个像素点,灰度值 ( 0 − 255 ) (0-255) (0−255)如下:
 每个点乘以对应的权重值:
每个点乘以对应的权重值:

得到

将这 9 9 9个值加起来,就是中心点的高斯模糊的值。
对所有点重复这个过程,就得到了高斯模糊后的图像。如果原图是彩色图片,可以对RGB三个通道分别做高斯平滑。
API:
cv2.GaussianBlur(src,ksize,sigmaX,sigmay,borderType)
参数:
src: 输入图像ksize:高斯卷积核的大小,注意 : 卷积核的宽度和高度都应为奇数,且可以不同sigmaX: 水平方向的标准差sigmaY: 垂直方向的标准差,默认值为0,表示与sigmaX相同borderType:填充边界类型
示例:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
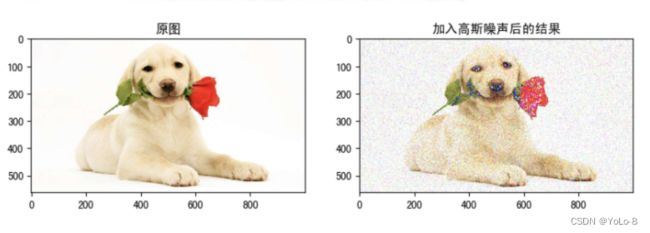
img = cv.imread('./image/dogGasuss.jpeg')
# 2 高斯滤波
blur = cv.GaussianBlur(img,(3,3),1)
# 3 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('高斯滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
2.3 中值滤波
中值滤波是一种典型的非线性滤波技术,基本思想是用像素点邻域灰度值的中值来代替该像素点的灰度值。
中值滤波对椒盐噪声(salt-and-pepper noise)来说尤其有用,因为它不依赖于邻域内那些与典型值差别很大的值。
API:
cv.medianBlur(src, ksize )
参数:
src:输入图像ksize:卷积核的大小
示例:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogsp.jpeg')
# 2 中值滤波
blur = cv.medianBlur(img,5)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('中值滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
总结
- 图像噪声
- 椒盐噪声:图像中随机出现的白点或者黑点
- 高斯噪声:噪声的概率密度分布是正态分布
- 图像平滑
- 均值滤波:算法简单,计算速度快,在去噪的同时去除了很多细节部分,将图像变得模糊
cv.blur()
- 高斯滤波: 去除高斯噪声
cv.GaussianBlur()
- 中值滤波: 去除椒盐噪声
cv.medianBlur()





