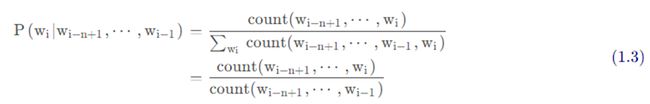人工智能自然语言处理：N-gram和TF-IDF模型详解

人工智能自然语言处理：N-gram和TF-IDF模型详解

1.N-gram 模型

N-Gram 是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为 N 的滑动窗口操作，形成了长度是 N 的字节片段序列。

每一个字节片段称为 gram，对所有 gram 的出现频度进行统计，并且按照事先设定好的阈值进行过滤，形成关键 gram 列表，也就是这个文本的向量特征空间，列表中的每一种 gram 就是一个特征向量维度。

该模型基于这样一种假设，第 N 个词的出现只与前面 N-1 个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计 N 个词同时出现的次数得到。常用的是二元的 Bi-Gram 和三元的 Tri-Gram。

当 n=1 时，一个一元模型为：

$P(w1,w2,\cdots ,wm)=\prod i=1mP(wi)$

当 n=2 时，一个二元模型为：

$P(w1,w2,\cdots ,wm)=\prod i=1mP(wi\mid wi-1)$

当 n=3 时，一个三元模型为：

$P(w1,w2,\cdots ,wm)=\prod i=1mP(wi\mid wi-2,wi-1)$

一个 n-gram 是 n 个词的序列：
一个 2-gram（bigram 或二元）是两个词的序列，例如 “I love”；
一个 3-gram（trigram 或三元）是三个词的序列，例如 “I love you”。
需要注意的是，通常 n-gram 即表示词序列，也表示预测这个词序列概率的模型。假设给定一个词序列（w1，w2，···，wm），根据概率的链式法则，可得公式 (1.1)：

$P(w1,w2,\cdots ,wm)=P(w1)\ast P(w2\mid w1)\cdots P(wm\mid w1,\cdots ,wm-1)=\prod i=1mP(wi\mid wi-2,wi-1)$

公式（1.1）右边的 P（wi | w1，w2，···，wi-1）表示某个词 wi 在已知句子 w1，w2，···，wi-1 后面一个词出现的概率

1.1 马尔科夫假设

在实践中，如果文本的长度较长时，公式（1.1）右边的 $P（wi|w1，w2，\cdot \cdot \cdot ，wi-1$的估算会非常困难，因此需要引入马尔科夫假设。

马尔科夫假设是指，每个词出现的概率只跟它前面的少数几个词有关。比如，二阶马尔科夫假设只考虑前面两个词，相应的语言模型是三元（trigram）模型。应用了这个假设表明当前这个词仅仅跟前面几个有限的词有关，因此也就不必追溯到最开始的那个词，这样便可以大幅缩减上述算式的长度。
基于马尔科夫假设，可得公式 (1.2):

$P(wi\mid w1,\cdots ,wi-1)\approx P(wi\mid wi-n+1,\cdots ,wi-1)$

当 n = 1 时称为一元模型（unigram model），公式（1.2）右边会演变成 P(wi)，此时，整个句子的概率为：

$P(w1,w2,\cdots ,wm)=P(w1)\ast P(w2)\cdots P(wm)=\prod i=1mP(wi)$

当 n = 2 时称为二元模型（bigram model），公式（1.2）右边会演变成 P(wi | wi-1)，此时，整个句子的概率为：

$P(w1,w2,\cdots ,wm)=P(w1)\ast P(w2\mid w1)\cdots P(wm\mid wm-1)=\prod i=1mP(wi\mid wi-1)$

当 n = 3 时称为三元模型（trigram model），公式（1.2）右边会演变成 P(wi| wi-2,wi-1)，此时，整个句子的概率为：

$P(w1,w2,\cdots ,wm)=P(w1)\ast P(w2\mid w1)\cdots P(wm\mid wm-2,\cdots ,wm-1)=\prod i=1mP(wi\mid wi-2,wi-1)$

估计 n-gram 模型概率采用极大似然估计（maximum likelihood estimation，MLE）。即通过从语料库中获取计数，并将计数归一化到（0，1），从而得到 n-gram 模型参数的极大似然估计。即：

其中 $count（Wi-n+1，\cdot \cdot \cdot ，Wi）$表示文本序列$（Wi-n+1，\cdot \cdot \cdot ，Wi）$，在语料库中出现的次数。

1.2 N-gram 模型优缺点

总结下基于统计的 n-gram 语言模型的优缺点：

• 优点：

  1. 采用极大似然估计，参数易训练；
  2. 完全包含了前 n-1 个词的全部信息；
  3. 可解释性强，直观易理解；

• 缺点：

  1. 缺乏长期依赖，只能建模到前 n-1 个词；
  2. 随着 n 的增大，参数空间呈指数增长；
  3. 数据稀疏，难免会出现 OOV 词（out of vocabulary）的问题；
  4. 单纯的基于统计频次，泛化能力差

2.TF-IDF

TF-IDF(term frequency-inverse document frequency，词频 - 逆向文件频率) 是一种用于信息检索 (information retrieval)) 与文本挖掘 (text mining) 的常用加权技术。它是一种统计方法，用以评估一个字或词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。

在信息检索 (Information Retrieval)、文本挖掘(Text Mining) 以及自然语言处理 (Natural Language Processing) 领域，TF-IDF 算法都可以说是鼎鼎有名。虽然在这些领域中，目前也出现了不少以深度学习为基础的新的文本表达和算分 (Weighting) 方法，但是 TF-IDF 作为一个最基础的方法，依然在很多应用中发挥着不可替代的作用。

TF-IDF 的主要思想是：如果某个单词在一篇文章中出现的频率 TF 高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。

• TF（全称 TermFrequency），中文含义词频，即关键词出现在网页当中的频次。

• IDF（全称 InverseDocumentFrequency），中文含义逆文档频率，即该关键词出现在所有文档里面的一种数据集合。

• TF-IDF 的计算过程为：

  1. 第一步，计算词频。
     词频（TF）= 文章的总词数某个词在文章中的出现次数​
     或者
     词频（TF）= 该文出现次数最多的词出现的次数某个词在文章中的出现次数​

  2. 第二步，计算逆文档频率。
     逆文档频率（IDF）=log(包含该词的文档数 +1 语料库的文档总数​)
     如果一个词越常见，那么分母就越大，逆文档频率就越小越接近 0。分母之所以要加 1，是为了避免分母为 0（即所有文档都不包含该词）。log 表示对得到的值取对数。

  3. 第三步，计算 TF-IDF。
     TF−IDF= 词频（TF）× 逆文档频率（IDF）

可以看到，TF-IDF 与一个词在文档中的出现次数成正比，与该词在整个语言中的出现次数成反比。所以，自动提取关键词的算法就是计算出文档的每个词的 TF-IDF 值，然后按降序排列，取排在最前面的几个词。

2.1 TF-IDF 算法总结

TF-IDF 算法是一种常用的文本特征表示方法，用于评估一个词对于一个文档集或语料库中某个文档的重要程度，常用于以下领域：

（1）搜索引擎；
（2）关键词提取；
（3）文本相似性；
（4）文本摘要。

• TF-IDF 算法优点：

  1. 简单有效：TF-IDF 算法简单易实现，计算速度快，并且在很多文本相关任务中表现良好。

  2. 考虑词频和文档频率：TF-IDF 综合考虑了词频和文档频率两个因素，可以准确表示词语在文档中的重要性。

  3. 强调关键词：TF-IDF 算法倾向于给予在文档中频繁出现但在整个语料库中较少见的词更高的权重，从而能够突出关键词。

  4. 适用性广泛：TF-IDF 算法可以应用于各种文本相关任务，如信息检索、文本分类、关键词提取等。

• TF-IDF 算法缺点：

  1. 无法捕捉语义信息：TF-IDF 算法仅根据词频和文档频率进行计算，无法捕捉到词语之间的语义关系，因此在处理一些复杂的语义任务时可能效果有限。

  2. 忽略词序信息：TF-IDF 算法将文本表示为词语的集合，并忽略了词语之间的顺序信息，因此无法捕捉到词语顺序对于文本含义的影响。

  3. 对文档长度敏感：TF-IDF 算法受文档长度的影响较大，较长的文档可能会有较高的词频，从而影响到特征权重的计算结果。

  4. 词汇表限制：TF-IDF 算法需要构建词汇表来对文本进行表示，词汇表的大小会对算法的性能和计算开销产生影响，同时也可能存在未登录词的问题。

  5. 主题混杂问题：在包含多个主题的文档中，TF-IDF 算法可能会给予一些频繁出现的词较高的权重，导致提取的关键词并不完全与文档主题相关。

3.关键知识点总结：

1. 在N-gram模型中，N表示表示每次取出的单词数量

2. 在N-gram模型中，当N取值越大，模型的效果会不一定变得更好（要合适）

3. N-gram模型可以用于文本分类、语音识别和机器翻译等自然语言处理任务。

4. N-gram模型的主要优点是可以捕捉上下文信息，但缺点是无法处理未知的单词。

5. 在TF-IDF模型中，IDF值越大代表该词对文本内容的区分度越高

6. 在TF-IDF模型中，词频（TF）指的是某个词在一篇文档中出现的次数。

本分类、语音识别和机器翻译等自然语言处理任务。

4. N-gram模型的主要优点是可以捕捉上下文信息，但缺点是无法处理未知的单词。

5. 在TF-IDF模型中，IDF值越大代表该词对文本内容的区分度越高

6. 在TF-IDF模型中，词频（TF）指的是某个词在一篇文档中出现的次数。