C++毕业设计——基于C++的RSA文件加密软件设计与实现（毕业论文+程序源码）——RSA文件加密软件

基于C++的RSA文件加密软件设计与实现（毕业论文+程序源码）

大家好，今天给大家介绍基于C++的RSA文件加密软件设计与实现，文章末尾附有本毕业设计的论文和源码下载地址哦。需要下载开题报告PPT模板及论文答辩PPT模板等的小伙伴，可以进入我的博客主页查看左侧最下面栏目中的自助下载方法哦

文章目录：

1、项目简介

1. 分析RSA算法的应用现状，论证文件加密应用RSA算法的可行性和意义。设计一套完整实用的RSA文件加密解决方案，具体编码实现。对RSA算法进行研究，从常规RSA算法出发，用C++实现RSA加密算法类库，并在32位windows平台封装成组件。在.Net平台引用此组件，实现可以对任意文件进行RSA加密操作的窗体应用程序。经过加密的文件以及密钥文件都是文本文件。给出关键类类图、整个应用程序的结构描述文档、关键模块流程图、较详细的接口文档、所有源代码。对应用程序进行测试，对测试结果进行分析研究，进而对应用程序进行改进，对关键算法进行尽可能的优化，最终得到一个在windows运行的可以用指定密钥对任意文件进行RSA加密并可解密的完整应用程序，和一些相关的可移植组件。

---

2、资源详情

项目难度：中等难度
适用场景：相关题目的毕业设计
配套论文字数：20204个字40页
包含内容：整套源码+完整毕业论文

---

3、关键词

RSA RSA算法 文件加密 加密成文本

---

4、毕设简介

提示：以下为毕业论文的简略介绍，项目源码及完整毕业论文下载地址见文末。

前 言
RSA公钥加密算法是第一个既能用于数据加密也能用于数字签名的算法。它易于理解和操作，也十分流行。算法的名字以发明者的姓氏首字母命名：Ron Rivest, Adi Shamir 和Leonard Adleman。虽然自1978年提出以来，RSA的安全性一直未能得到理论上的证明，但它经历了各种攻击，未被完全攻破。随着越来越多的商业应用和标准化工作，RSA已经成为最具代表性的公钥加密技术。VISA、MasterCard、IBM、Microsoft等公司协力制定的安全电子交易标准（Secure Electronic Transactions，SET）就采用了标准RSA算法，这使得RSA在我们的生活中几乎无处不在。网上交易加密连接、网上银行身份验证、各种信用卡使用的数字证书、智能移动电话和存储卡的验证功能芯片等，大多数使用RSA技术。

当今公钥加密更广泛应用于互联网身份认证，本课题将公钥加密算法RSA应用于小型文件加密。将任意文件加密成文本的解决方案，使其使用更加灵活。整个工程的分层设计，给引用移植和后续开发带来便利。

第1章 RSA应用现状及应用于文件加密的分析
1.1 RSA算法介绍与应用现状
RSA算法可以简单叙述如下：
<密钥生成>
取素数p，q，令n=p×q.
取与(p-1)×(q-1)互素的整数e，
由方程d×e=1 (mod (p-1)×(q-1))解出d，
二元组(e,n)作为公开密钥，
二元组(d,n)作为私有密钥．
<加密解密>
b=ae mod n，c=bd mod n.
附录中给出了证明a=c (mod n).
(具体的RSA算法协议见http://www.di-mgt.com.au/rsa_alg.html ，提及的算法中的字母与协议文档中的一致，不再另做解释)
RSA公开密钥加密算法自20世纪70年代提出以来，已经得到了广泛认可和应用。发展至今，电子安全领域的各方面已经形成了较为完备的国际规范。RSA作为最重要的公开密钥算法，在各领域的应用数不胜数。RSA在硬件方面，以技术成熟的IC应用于各种消费类电子产品。

RSA在软件方面的应用，主要集中在Internet上。加密连接、数字签名和数字证书的核心算法广泛使用RSA。日常应用中，有比较著名的工具包Open SSL(SSL，Security Socket Layer,是一个安全传输协议，在Internet上进行数据保护和身份确认。Open SSL是一个开放源代码的实现了SSL及相关加密技术的软件包，由加拿大的Eric Yang等发起编写的。相关详细介绍见http://www.openssl.org/about/ )。Open SSL应用RSA实现签名和密钥交换，已经在各种操作系统得到非常广泛的应用。另外，家喻户晓的IE浏览器，自然也实现了SSL协议，集成了使用RSA技术的加密功能，结合MD5和SHA1，主要用于数字证书和数字签名，对于习惯于使用网上购物和网上银行的用户来说，几乎天天都在使用RSA技术。

RSA更出现在要求高度安全稳定的企业级商务应用中。在当今的企业级商务应用中，不得不提及使用最广泛的平台j2ee。事实上，在j2se的标准库中，就为安全和加密服务提供了两组API：JCA和JCE。 JCA (Java Cryptography Architecture)提供基本的加密框架，如证书、数字签名、报文摘要和密钥对产生器； JCA由几个实现了基本的加密技术功能的类和接口组成，其中最主要的是java.security包，此软件包包含的是一组核心的类和接口，Java中数字签名的方法就集中在此软件包中。JCE(Java Cryptography Extension) 在JCA的基础上作了扩展，JCE也是由几个软件包组成，其中最主要的是javax.crypto包，此软件包提供了JCE加密技术操作API。javax.crypto中的Cipher类用于具体的加密和解密。在上述软件包的实现中，集成了应用RSA算法的各种数据加密规范(RSA算法应用规范介绍这些API内部支持的算法不仅仅只有RSA，但是RSA是数字签名和证书中最常用的)，用户程序可以直接使用java标准库中提供的API进行数字签名和证书的各种操作。

单机应用程序使用RSA加密尚比较少见，例如使用RSA加密任意一个文件。

1.2 RSA应用于文件加密的分析
1.2.1 文件加密使用RSA的可行性
通过1.1节的论述，不难看出RSA当今的应用多在于数字签名和证书等方面。之所以只应用于这些短小数据的加密解密，是因为RSA算法加密极慢，速度是DES对称密钥加密速度的千分之一左右。正是因为这样，把RSA应用于普通文件加密的想法一直被忽略。通常文件被想象成大数据块，但是实际上在日常应用中，有些极其重要的文本资料是并不太大的，比如因担心遗忘而用普通文本记录的银行帐号和密码、不应被陌生人知道的重要电话号码、几千字节大的重要小图片等。

虽然RSA加密运算的速度十分慢，但是在PC性能越来越好的今天，对于几千字节的数据进行一次几百位密钥的RSA加密，所消耗的时间应该是可以接受的。下面结合大数运算程序的调试，从理论上简单的分析消耗时间。在一台普通配置的PC机上对一个整数进行幂模运算，因为公开密钥的e通常取的较小，所以指数取一个小整数，比如C353，模一个70字节长的整数(140位十六进制，大数单元以线性组方式实现，对应到RSA算法中，这相当于约560bit的n)，调试一个函数测试，按初等数论中的知识对程序进行算法优化，最终在一台配置为AMD Athron2800+，外频333MHZ，物理内存512MB的PC上测试需要约45毫秒时间。如果按这种速度，逐字节对1KB的数据进行同样的运算，所消耗的时间理论上为45毫秒的1024倍即约45秒。这个时间并不是非常长。

其实从一个简单的角度来说，既然RSA用于数字签名可行，那就完全可以用于同样大小的普通文件。对于较大的文件，如果分成与数字签名同样大小的段(这里假设数字签名较短，不分段一次计算加密完成)，分开的各段逐一进行加密运算，那所需要的时间也只是按文件大小线性的增长。通常数字签名为几十字节，加密运算并不需要很长的等待，这就说明对于几百字节或一两K字节大小的文件来说，如果进行RSA加密，并不会是非常漫长的工作。当然，如果文件更大，加密就显得十分漫长了。比如按前面叙述的45毫秒大数运算程序推理，加密1M字节大小的文件需要约1天的时间。所以，要在普通PC用几百位以上的长密钥RSA加密文件，文件不能过大，一般可以接受的上限是几KB。如果要在较短时间内加密大文件，需要缩短密钥长度以减小运算量，这将带来安全性隐患。

本文的第3章将根据实际调试好的软件，测试给出具体的时间消耗数据。例如，在一台配置为AMD Athron2800+，外频333MHZ，物理内存512MB的PC上测试实现的软件，以560bit的n逐字节加密一个1KB大小的文件需要55秒。通常记录如银行帐号密码等重要数据的文本文件大小不足百字节，加密只需要数秒钟。所以对于小型文件，进行较长密钥的RSA加密是完全可行的。

1.2.2 文件加密使用RSA的意义
如1.2.1节所述，小型文件加密可以使用RSA。比如，因担心遗忘而用普通文本记录的银行帐号和密码、不应被陌生人知道的重要电话号码、几千字节大的重要小图片等。可行的方法未必是必要的，本小节讨论何种文件适合用非对称密钥加密，即RSA加密文件的意义所在。
省略

第2章 RSA文件加密软件的设计与实现
2.1 需求分析与总体设计
2.1.1 功能分析
经过1.2.2节的论述，我们可以将对软件的要求总结如下：
① 可以按要求的位数生成非对称密钥。
② 可以保存密钥和装载密钥，密钥保存为纯文本。
③ 可以用指定密钥以RSA算法加密任意一个文件，加密生成的数据为纯文本。
④ 可以装载加密过的文件，并用指定的密钥解密还原出原文件。
⑤ 提示信息完整、操作舒适、图形界面雅观

按上述描述，给出Use Case和Statechart如图2-1。

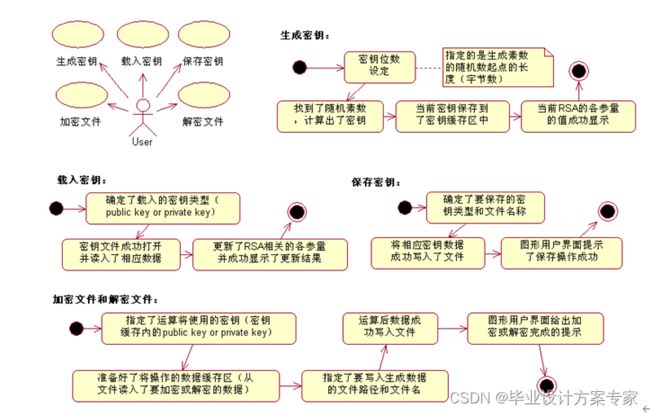
图2-1 本项目的 Use Case和Statechart
根据以上分析，一般来说，需要进行编码的程序有
①RSA密钥生成 ②RSA加密解密 ③任意文件的读取和保存操作 ④各环节必要的数据编码转换 ⑤图形操作界面。

2.1.2 工程方案选择
结合现有的常见开发模式综合分析，有多种实现方案，下面陈述其中几种，并分析选择一种解决方案，并给出工程框架。

1. 整个工程使用java平台实现
   RSA密钥生成、RSA加密解密的功能实现十分简单，因为标准库中集成几乎所有功能，不需要从RSA算法出发进行编码。在j2se标准库中，javax.crypto中的Cipher类用于具体的加密和解密，java.security包直接提供了数字签名的相关方法。因为有强大的标准库支持，文件的读取和保存操作、各环节必要的数据编码转换、图形操作界面的实现也很简单(使用java.io java.awt或javax.swing 等包)，如果结合一种快速开发的IDE，比如JBuilder，整个软件可以在很短的时间内编码完成。如果不考虑非PC设备和机器效率等问题，java平台几乎是最佳解决方案。但是缺点也很明显，如果想把核心算法和功能应用到非PC设备(例如嵌入式手持设备)，则要求设备上有支持前面提及的加密类库的CVM；对于在PC上运行，JVM的数据运算速度要远远落后于本地化代码在PC上的运算速度，本软件需要进行大量运算，这一点不适合由java完成。

2. 整个工程使用.Net平台实现
   与使用java平台完全类似，加密等有.Net基础类库的支持，不需要大量编码实现，另外由于Visual Studio的强大便利，这种规模的工程可以十分迅速的完成。缺点是只能在有微软.Net Framework的环境运行，在Windows操作系统，.Net Framework的机器效率好于java平台，但是相比于本地化的代码，还是十分拖沓的。

3. 整个工程使用Windows本地化程序实现
   在不应用Windows或第三方现成组件的情况下，需从RSA算法出发编码实现。其他各功能的设计开发，如文件操作、数据编码转换和图形界面等，可以使用ATL、MFC或Windows API实现。这种工程几乎是为Windows量身订做，执行效率最好。但是对于非PC设备，只能方便的移植到运行Windows嵌入式操作系统的设备，向其他操作系统移植困难，需要重新编写大量代码。通常解决本地化代码的移植问题，都是使用C++标准库，即功能尽量多的由C++标准库完成，这样在移植的时候，只需要重新编写操作系统相关的代码即可。这种开发方式比起前两种，缺点就是设计开发模式陈旧，代码烦琐，不方便维护；流行的.Net上的语言引用各种功能比较麻烦。

4. 考虑可能的复用，针对具体情况分层开发实现
   综合考虑复用性、可维护性和执行效率，较妥当的方法是分层设计。核心的RSA算法由C++类库实现，针对用户所在的操作系统封装成本地化组件。其他各功能如文件操作、数据编码转换和图形界面等，由托管代码借助虚拟机平台标准库的功能快速开发实现(本文针对选用.Net上的C#论述，选用java由JNI或其他方式调用本地组件，设计模式上是完全类似的)。这种开发方式，核心功能集中在最底层，在不断的封装中针对具体环境对组件功能不断扩充，任意一个层面的封装都可以被直接应用到其他项目，比如在Web使用以前为某窗体程序写的组件、给嵌入式设备交叉编译算法库等。但是每一层都需要依赖底层的所有组件。图2-2形象的说明了分层设计给复用带来的好处。
   

图2-2 综合考虑复用性、可维护性和执行效率的分层设计
选用第四种设计方案，上层使用C#，底层算法使用C++，可以由一个Visual Studio解决方案管理，给调试带来极大的方便。整个工程分四层，实现RSA加密算法的C++核心类库、封装C++核心类库的DLL组件、引用DLL的.Net类、实现文件操作功能的.Net窗体应用程序。2.2节详细介绍各部分的设计与开发。

考虑到工作量，本软件加解密数据没有严格遵从RSA标准PKCS #1，而是在满足设计要求的前提下，以一种尽可能简单的方式实现加密和解密。

2.2 各部分的设计与开发
2.2.1 实现RSA加密算法的C++核心类库

1. 大数存储和四则运算
   根据RSA算法的要求，为了实现大数的各种复杂运算，需要首先实现大数存储和基本四则运算的功能。当今开源的大数运算C++类有很多，多用于数学分析、天文计算等，本文选用了一个流行的大数类型，并针对RSA算法和本项目的具体需要对其进行了扩充和改进。下面简单介绍大数存储和四则运算的实现原理。

最先完成的功能是大数的存储，存储功能由flex_unit类提供。和普通的类型一样，每一个大数对应一个flex_unit的实例。类flex_unit中，用一个无符号整数指针unsigned * a指向一块内存空间的首地址，这块内存空间用来存储一个大数，所以可以说，大数是被存储在一个以unsigned为单元的线性组中。在方法void reserve( unsigned x )中通过C++的new来给a开辟空间，当flex_unit的实例中被存入比当前存储的数更大的数时，就会调用reserve来增加存储空间，但是当flex_unit的实例中被存入比当前存储的数更小的数时，存储空间并不会自动紧缩，这是为了在运算的时候提高执行效率。结合指针a，有两个重要的无符号整数来控制存储，unsigned z和unsigned n，z是被分配空间的单元数，随数字变大不断增大，不会自己紧缩，而n是当前存储的大数所占的单元数，组成一个大数的各unsigned单元的存入和读出由set、get方法完成，变量n是只读的。类型unsigned在32位机是32位的，所以对于flex_unit这个大数类来说，每个大数最大可以达到 个字节长，这已经超过了32位机通常的最大内存容量，所以是足够进行RSA所需要的各种运算的。图2-3形象的说明了大数存储类flex_unit对大数的管理。

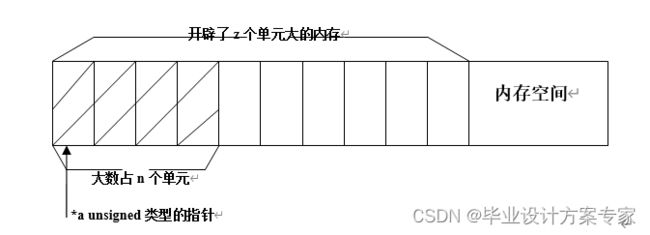
图2-3 flex_unit对大数的管理
在flex_unit的存储功能基础上，将其派生，得到vlong_value，在vlong_value中实现四则运算函数，并实现强制转换运算符unsigned，以方便大数类型和普通整数的互相赋值。当大数被强制转换为unsigned时，将取其最低四字节的值。四则运算实现的原理十分简单，都是按最基本的算术原理实现的，四则运算过程的本质就是按一定数制对数字的计算，比如相加，就是低位单元对齐，逐单元相加并进位，减法同理。而乘除法和取余也都是按照竖式运算的原理实现，并进行了必要的优化。虽然实现了四则运算函数，但是若是程序里的运算都要调用函数，显得烦琐而且看起来不美观，所以我们另写一个类vlong，关联(Associate，即使用vlong_value类型的对象或其指针作为成员)vlong_value，在vlong重载运算符。这样，当我们操作vlong大数对象的时候，就可以像使用一个简单类型一样使用各种运算符号了。之所以将vlong_value的指针作为成员而不是直接构造的对象，也是为了提高执行效率，因为大型对象的拷贝要消耗不少机器时间。

2 大数幂模与乘模运算•Montgomery幂模算法
在实现了vlong类型后，大数的存储和四则运算的功能都完成了。考虑到RSA算法需要进行幂模运算，需要准备实现这些运算的方法。所以写一个vlong的友元，完成幂模运算功能。幂模运算是RSA 算法中比重最大的计算，最直接地决定了RSA 算法的性能，针对快速幂模运算这一课题，西方现代数学家提出了很多的解决方案。经查阅相关数学著作，发现通常都是依据乘模的性质 ，先将幂模运算化简为乘模运算。
省略

3 寻找素数•Eratosthenes筛选与Fermat素数测试
首先要说明的是，事实上，当今的计算机还不足以聪明到立刻计算生成一个很大的随机素数。一般来说，要得到100%准确的大素数，都是通过查已经计算好的素数表的方式。但是素数表的方式给RSA的安全性带来隐患，因为攻击者如果得到了密钥生成时所使用的素数表，攻破RSA加密的难度将会大大降低。本程序起初使用素数表的方式，后来考虑到安全性问题，生成密钥的方式改为随机计算生成。这样，短时间内如果要得到一个100%准确的大素数是很困难的，只能以尽可能高的概率得到一个大素数。

经过2.2.1.1和2.2.1.2小节，所有的大数运算功能都准备完毕，在此基础上，本工程将寻找素数的功能置于类Prime_factory_san之中。外部只要调用本类实例的成员vlong find_prime( vlong & start )就可以以大数start为起点，得到一个数，这个数是素数的概率很大。下面介绍寻找素数的原理。

首先在需要寻找素数的整数范围内对整数进行筛选，把所有确知为合数的整数排除出去。程序中构造了一个数组b[]，大小为一轮素数搜索的范围，记搜索范围大小为SS。b[0]到b[SS]分别对应大数start到start+SS。b[]中所有元素先初始化为1，如果对应的大数确定为合数，就将b[]中对应的元素置为0。最后，只需对那些b[]中为1的元素对应的大数进行比较确切的素数测试即可，只要被测试的数是素数概率达到一定门限，就判这个数为素数。这样做既保证了这段程序可以在短时间内执行完，又保证了可以以比较高的准确度得到素数。

函数find_prime先把b[]的所有元素赋值为1，然后按参数start给标记数组b[]的各元素赋0值。下面描述标记数组b[]的赋0值算法。首先，在类Prime_factory_san被构造的时候，构造函数中从2开始搜寻一些小素数，记录在数组pl[]中，共记录NP个。这些小素数用来当作因子，他们的倍数将被从大素数搜索范围内剔除(即把数组b[]的对应元素标记为0)，剔除的程序代码如下。

for (i=0;i<np;i++)
{
  unsigned p = pl[i];
  unsigned r = start % vlong(p);
  if (r) r = p - r;
  while ( r < SS )
  {
    b[r] = 0;
    r += p;
  }
}

这里利用start对各小素数因子p求模的办法，得到当前p在素数搜索范围内的最小倍数在b[]中的对应位置，将其剔除后，不断后移p个位置，将这个小素数因子p在搜索范围内的所有倍数全部剔除，如图2-5所示。在完成对所有小素数因子的类似操作后，他们的倍数在搜索范围内的位置标记b[r]被全部标记为0。实际上这就是Eratosthenes筛选法。

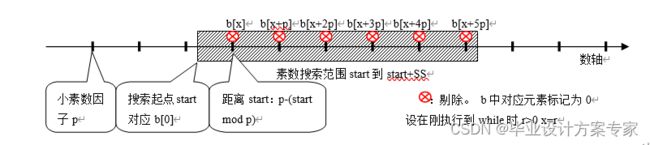
图2-5 在素数搜索范围内剔除小素数因子p的倍数
接下来，对可能为素数的数(即标记数组b[]中值为1的元素对应的数)进行素数测试。数论学家利用费马小定理研究出了多种素数测试方法，本程序使用一种最简单的方式，直接应用费马小定理。取一个与p互素的整数A，对于大素数p来说应该满足Ap-1mod p=1，但是我们把p代入一个大整数，满足这个关系的数不一定是素数。这时我们改变A，进行多次测试，如果多次测试都通过，这个数是素数的概率就比较大。按这种原理，我们编写素数测试函数如下。

int is_probable_prime_san( const vlong &p )
{
  const rep = 4; //测试次数
  const unsigned any[rep] = { 2,3,5,7 }; //测试用的底数
  for ( unsigned i=0; i<rep; i+=1 )
if ( modexp( any[i], p-vlong(1), p ) != vlong(1) ) return 0;
 //modexp是幂模函数，按上一小节叙述的算法编码。
//这里modexp计算any[i]p-1mod p。
  return 1;
}

测试通过，程序就判定这个数为找到的素数，将找到的素数返回给上层程序使用。在这里其实有一个不可忽视的问题，就是得到一个测试通过的合数。对于这种情况，RSA算法加密解密是否还可以实现，是一个需要从数学角度论证的问题。因为得到素数的概率很高，经过一整天的生成密钥和加密操作，没有发现失败的密钥， 所以本文暂没有对这个问题进行讨论。
综上所述，总结素数寻找的流程，如图2-6所示。

图2-6 函数find_prime寻找素数的流程框图
得到了大素数，即RSA算法中的p、q，我们就可以计算出密钥，进行加密等操作了。

4 二元一次不定方程
在RSA 算法中，往往要在已知A、M的情况下，求B的最小值，使得 (AB) mod M = 1。即相当于求解B、N都是未知数的二元一次不定方程 AB-MN=1的最小整数解。
而针对不定方程ax-by=1 的最小整数解，古今中外都进行过详尽的研究，西方有著名的欧几里德算法，即一种辗转相除法，中国有秦九韶的“大衍求一术”。欧几里德算法是一种递归算法，较容易理解。下面举例说明用欧几里德算法求解二元一次不定方程的最小整数解。
给定不定方程11x-49y=1，求最小的x
（1） 11 x - 49 y = 1 49 mod 11 = 5
（2） 11 x - 5 y = 1 11 mod 5 = 1
（3） x - 5 y = 1 5 mod 1 = 0
逆向代入：
令y=0 代入（3）得x=1
令x=1 代入（2）得y=2
令y=2 代入（1）得x=9
x=9;y=2即为所求。
程序中，全局函数vlong modinv( const vlong &a, const vlong &m )用来完成这种算法。对应前面的叙述，参数a对应A，参数m对应M，函数返回值即为B的最小值。

5 按常规RSA算法实现加密与解密
最后，类RSA_san基于前面的准备工作，实现RSA密钥生成和加解密的功能(算法在此不再赘述，RSA算法协议见http://www.di-mgt.com.au/rsa_alg.html)。为了方便阅读，整个类的源程序中，所使用的变量字母均和RSA算法协议中一致。在类RSA_san的构造函数里，执行准备一对随机密钥的操作。之后可以直接使用类的其他成员进行RSA加解密操作，也可以载入以前保存的密钥或再次随机生成密钥。类中各成员频繁的用到字符串和vlong类型的转换，因为大数是用字符串置入的，而把大数读出，也是保存在字符指针指向的一段内存空间里，所以也是字符串。所以，需要实现一系列的编码转换函数，比如将unsigned指针指向的一段空间里保存的一个大数，表示成十六进制形式的字符串文本。编码转换通常是用C风格的指针操作和sprintf函数来完成。

需要加密和解密的数据也是通过字符串参数置入的。由于字符串的结尾字符“\0”实际上也可能是需要加密的数据，所以置入的串长度并不能以“\0”来决定，程序里引入一个unsigned类型的参数来决定置入的串长度，这样就解决了加密连0数据时候被截断的问题。
因为是对文件加密的软件，需要加密的数据通常并不止几字节，这时由上层程序将数据按用户的设置分块，分别加密或解密。本软件默认的分块大小是1字节，即逐个字节作为参数，调用C++核心模块中的方法。
加密解密流程均为标准RSA算法，具体过程和使用方法参见源程序和接口文档。

6 核心类库综述
综上几小节所述，实现RSA加密算法的C++核心类库由六个类组成，类名和对应的功能描述总结如表2-1所示。各个类之间的关系如图2-7所示。

表2-1 RSA加密算法的C++类库中的类

图2-7 C++核心功能类图
另外需要说明的是，程序中有几个不属于任何类的全局函数，比如应用辗转相除法求最大公约数的函数gcd、解同余方程的函数modinv等。按常规设计模式来说，不应当出现类之外的函数，但是因为这些函数使用频繁，考虑到机器效率，直接置于全局，不再另行包装。

2.2.2 封装C++核心类库的DLL组件
在Visual Studio当前的解决方案中以VC++创建一个win32dll工程，将测试好的实现RSA加密算法的C++核心类库中的所有文件加入到此工程下，新建一对cpp和h文件，把可能用到的功能全部规划为新文件中的全局函数，并以C接口导出，即__declspec(dllexport)。由于核心类库的对外功能都使由RSA_san类提供的，所以在新cpp文件中全局的声明一个RSA_san类的对象指针(RSA_san WRSA)，全局函数int start_RSA_san()初始化WRSA对象，在初始化成功后，其他全局函数通过调用*WRSA对象的公开方法实现各种功能，如加密、读取密钥等。在关闭上层引用程序以前，应执行int finish_RSA_san()来释放WRSA，该函数执行delete WRSA的操作。其他接口函数的使用见DLL接口文档。

另外，DLL组件可以自己在全局函数中实现一些其他功能，作为对核心类库功能的补充。C接口的DLL组件可以被诸如VB、Delphi等开发环境方便的引用。

2.2.3 引用DLL的.Net类与实现文件操作功能的窗体应用程序
在C#编写的.Net类里，使用特性[DllImport(“sanpack_rsa.dll”)]引用C接口的DLL组件。类中接口DLL的函数都以静态成员的方式对外公开，其他.Net程序可以直接使用。在类库中还提供了任意长度随机串的生成函数，此函数用于生成寻找素数的大数起点。
文件操作使用.Net基础类库中的System.IO中的类实现。一般因为文件操作十分简单，用流输入输出的方式包装完成，程序中将文件操作直接放在菜单项关联的事件处理函数中。
窗体等图形操作界面直接由Visual Studio的所见即所得的方式完成，不需要编码实现。

最终实现的应用程序，结构如图2-8所示。

图2-8 本软件的Visual Studio解决方案

第3章 软件整体测试与分析改进
3.1 编写测试各项性能需要的精确计时类
由于.Net基础类库提供的计时功能十分不精确，无法胜任软件性能测试的工作，这里使用Windows API 函数QueryPerformanceCounter和QueryPerformanceFrequency进行精确计时。功能被封装在C#类HighResolutionTimer中，使用时只需构造一个此类的对象，在计时开始的时候调用其Start方法，计时结束时调用其Stop方法，然后访问其ElapsedTime属性，就可以得到一个以秒为单位的float型精确的计时值了。API 函数QueryPerformanceCounter和QueryPerformanceFrequency是靠查询CPU的高精度计时器来计时的，所以可以轻松的精确到毫秒级计时。

附录中给出了这个类的源代码。
3.2 测试数据与分析改进
3.2.1 密钥生成测试
生成密钥运算最费时的工作是寻找素数。如2.2.1.3小节所叙述，寻找素数是一项颇为复杂的工作，其速度可能受以下变量的影响：RSA加密需要的n的位数（寻找素数的整数起点大小start）、大素数测试时底数A的个数（针对一个整数的素数测试次数）、小素数因子p的个数NP、一轮寻找遍历的整数个数SS等。其中最具影响力的因素显然是RSA加密需要的n的位数。以下对各变量分别进行测试，暂且忽略操作系统调度对测试的影响。
1 测试加密使用的n的位数对耗时的影响
即 在固定A、NP、SS等变量的情况下，改变加密位数n，测试密钥生成的时间消耗情况。测试时，A取4个值，分别为2、3、5、7，NP取200，SS取1000。测试PC配置为CPU CR1.7GHZ/外频100MHZ/物理内存512MDDR/MSI6398主板845 Ultra-AD芯片组，下文测试中，未说明PC配置的也都在同一PC完成，不再重复。统计数据如表3-1所示。表中各项对应的全部测试数据见http://3mn.net/www/download/RSAkeygen_n-Ttest.txt ，包括两个作为素数搜索起点的随机数和生成的素数p、q以及e、d、n。
省略

3.2.3 加密解密测试
进行对任意文件加密与解密的测试，这里给出几组从不同角度进行测试的数据。下面除了第3组测试，其他都是把文件逐字节进行RSA运算，逐字节加密是本软件的默认设置。
省略
3.2.4 性能分析与改进优化
经过一系列的RSA密钥生成、文件输入输出和加密解密测试，做简要的性能分析如下。
① 软件消耗时间的运算，大部分集中在C++核心类库，即RSA相关的各种运算。其中，幂模运算和寻找素数对时间的消耗最大，在核心优化时应优先考虑。
② 文件输入输出消耗时间其次，因为磁盘读写速度要远远低于内存读写速度。所以，应该将频繁的读写操作尽量集中到内存，然后一次性写入磁盘。

针对以上两点，软件应进行一系列改进和优化。主要有以下几方面。
① 在要对文件进行加密解密的时候，先将文件按一定的数据结构读入内存，然后进行加密或解密操作。运算数据都读取自内存。
② 在对加密或解密完成的数据进行写出的时候，都是将其直接写到指定好的文件，即直接写入磁盘。这是因为，考虑到中途可能因为意外断电等原因引起操作中断，为了保护已经花费时间运算完成的数据，将其直接写入磁盘。
③ 在关键算法上做进一步优化，例如在寻找素数时，素数测试使用更快速的算法；还有3.3节提到的，在用私有密钥进行幂模运算时使用中国余数定理等。
④ 对C++核心类库进行重点优化，使其运算效率尽可能提高。其中包括对各类之间的组织细节、各程序模块的具体编写等，进行全面细致的检查和修改，例如将大数据类型以对象指针传递而不拷贝，将简单的for循环展开等。
由于开发时间仓促等因素，在书写本文时，软件并未完成全面细致的优化。
3.3 使用中国余数定理
对于用RSA加密解密的一方，是计算 。这里n＝p×q，p和q是两个二进制长度接近的大素数。由于用私密密钥加密或解密的一方实际知道n的分解，即p和q，所以这一计算可以分解为以下两部分分别进行 (附录中有中国余数定理的简单介绍) 。
省略

谢 辞
省略

参考文献
1．华罗庚，数论导引，科学出版社， 1979．
2．Montgomery PL， Modular multiplication without trialdivision［J］， Mathematics of Computation， 1985， 44(170)：519–521．
3．Oh JH，Moon S J， Modular multiplication method［J］， IEE Proceedings：Computers and Digital Tech－niques， 1998， 145(4)：317–318．
4．施向东 董平，基于RSA算法的一种新的加密核设计，微计算机信息 2005年第12-3期 中图分类号：TP289文章编号：1008-0570(2005)12-3-0039-03 页码39-41 < http://www.autocontrol.com.cn/magazine/3845.html >
5．[AX931] ANSI X9.31-1998 Digital Signatures using Reversible Public Key Cryptography for the Financial Services Industry (rDSA)， Appendix A， American National Standards Institute， 1998．
6．[COCK73] Clifford Cocks. A Note on ‘Non-Secret Encryption’， CESG Research Report， 20 November 1973， < http://www.cesg.gov.uk/publications/media/nsecret/notense.pdf >．
7．[KALI93] Burton Kalinski. Some Examples of the PKCS Standards， RSA Laboratories， November 1993， < ftp://ftp.rsasecurity.com/pub/pkcs/ascii/examples.asc >．
8．[PKCS1] RSA Laboratories. PKCS #1 v2.1: RSA Encryption Standard. June 2002， < ftp://ftp.rsasecurity.com/pub/pkcs/pkcs-1/pkcs-1v2-1.pdf >．
9．[RIVE78] R. Rivest， A. Shamir and L. Adleman. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems．Communications of the ACM， 21 (2)， pp. 120-126， February 1978．
10．陈发来，中国科学技术大学数学系 数学实验——素数 < http://www.teach.ustc.edu.cn/jpkc/guojia/sxsy/skja/exp5.ppt >

附 录

在C#使用Windows kernel32.dll中的API实现精确计时的类源代码
public class HighResolutionTimer
{
private long start;
private long stop;
private long frequency;
public HighResolutionTimer()
{
QueryPerformanceFrequency (ref frequency);
}
public void Start ()
{
QueryPerformanceCounter (ref start);
}
public void Stop ()
{
QueryPerformanceCounter (ref stop);
}
public float ElapsedTime
{
get
{
float elapsed = (((float)(stop - start)) / ((float) frequency));
return elapsed;
}
}
[System.Runtime.InteropServices.DllImport(“KERNEL32.dll”, CharSet=System.Runtime.InteropServices.CharSet.Auto)]
private static extern bool QueryPerformanceCounter(ref long performanceCount);
[System.Runtime.InteropServices.DllImport(“KERNEL32.dll”, CharSet=System.Runtime.InteropServices.CharSet.Auto)]
private static extern bool QueryPerformanceFrequency(ref long frequency);
}

加密解密测试时使用的两组密钥
密钥位数并不精确，可能有几位的差距。
512bit私有密钥（两行分别为d、n）
11C6EBA27BEA0A998C517D522DAE7ADA203F7325576C97853584C9253CD867B0FD6217579F8240F7FCB7474F1B532B8532794605C704D94513B240700BF04C9
195F9E4D3ABD729F6C7E7B7B6AF58DA89A10147DB6ADF0F4F3FA988E4C2441C2130C449852A68E19E32768FB3B41775DD4EF97F92674F3D21547249CD6D70C5
512bit公开密钥（两行分别为e、n）
C359
195F9E4D3ABD729F6C7E7B7B6AF58DA89A10147DB6ADF0F4F3FA988E4C2441C2130C449852A68E19E32768FB3B41775DD4EF97F92674F3D21547249CD6D70C5
1024bit私有密钥（两行分别为d、n）
79113601A430BCE489C6CBD825161014211DCC3D090D86C8F56E0F6324C0994A4E22596588C08B38354BA08C31DB6857BF919B8A67FDC0054A2C5BC783EEDEC3C1900A3AE66FAE1498562C6953FD9B7E0DD6EA515FE190D8123C31933328F79A5F1C63320499D09A4AC8F242E06F6BE903349570CE902197E6B24F3B8AB7D59
90640C3AA06DEC9ED00B8C232812B96F51979338282E782E8A10C5650D162781AC030747B0DEF22C42078036DDC6D42BC5728F5300CD6EDA1FFEC01D1F0B4FC06117BEC185E6429CA536D7BFB9B7235C6CC42A5C50C0C4798A04705212FC345170DEAB00A03E27D26292B7DE39F63874DC4FEB13DBE9C40B6DB9B593869EFD3
1024bit公开密钥（两行分别为e、n）
C359
90640C3AA06DEC9ED00B8C232812B96F51979338282E782E8A10C5650D162781AC030747B0DEF22C42078036DDC6D42BC5728F5300CD6EDA1FFEC01D1F0B4FC06117BEC185E6429CA536D7BFB9B7235C6CC42A5C50C0C4798A04705212FC345170DEAB00A03E27D26292B7DE39F63874DC4FEB13DBE9C40B6DB9B593869EFD3

RSA算法可行性的证明
求证：
<命题1-1> 若 p, q 是相异素数, e×d ＝ 1 mod (p-1)×(q-1),
a 是任意一个正整数,
则有 c ＝ a mod (p×q)
证明：
∵ d×e ＝ 1 mod (p-1)×(q-1)
∴ d×e ＝ k×(p-1)×(q-1) + 1, 其中 k 是整数
∵ 在 mod 中是 preserve 乘法的 (x ＝ y mod z and u ＝ v mod z  x×u ＝ y×v mod z),
∴
首先，素数p、q要么能整除a，要么与a互素。

1. 如果 a 不是 p 的倍数, 也不是 q 的倍数时,
   则 (费马小定理)  (根据质数算术基本定理，a与素数p互素，则am也与p互素，m是整数)
   (费马小定理) 
   ∴ p, q 均能整除 - 1  p×q | - 1
   即 ＝ 1 mod p×q
    c ＝ ＝ a mod p×q
2. 如果 a 是 p 的倍数, 但不是 q 的倍数时,
   则 (费马小定理)
    ＝ 1 mod q
    c ＝ ＝ a mod q
    q | c - a
   ∵ p | a
    c ＝ ＝ 0 mod p
    p | c - a
   ∴ p×q | c - a  c ＝ a mod p×q
3. 如果 a 是 q 的倍数，但不是 p 的倍数时，证明同2理显然
4. 如果 a 同时是 p 和 q 的倍数时,
   则 p×q | a
    c ＝ ＝ 0 mod p×q
    p×q | c - a
    c ＝ a mod p×q
   证毕□
   费马小定理叙述：e 是任一素数, n 是任一整数, 则 ＝ n mod e (即如果 n 和 e 互质, 则 ＝ 1 mod e) 运用群论知识可以证出费马小定理。
   命题1-1说明 a 经过编码为 b 再经过解码为 c 时, a ＝ c mod n (n = p×q)，但在做编码解码时, 由于限制 0 <= a < n, 0 <= c < n, 此时显然 a ＝ c, 所以这个过程能做到编码解码的功能。

中国余数定理的简单介绍
令n=n1n2…nk，其中ni是两两互质的数，则对0<=a 首先定义mi=n/ni(i=1,2…k)，则mi是除了ni以外的所有nj的乘积，接下来令ci=mi与模n意义下mi的逆元的积，则a为(a1c1+a2c2+…+akck) (mod n)。
例如，已知a模5余2 且 模13余3，那么a1=2,n1=m2=5,a2=3,n2=m1=13，则有c1=13*(2 mod 5)=26，c2=5*(8 mod 13)=40，所以a=(226+340)（mod 65)=42。

---

5、资源下载

本项目源码及完整论文如下，有需要的朋友可以点击进行下载。如果链接失效可点击下方卡片扫码自助下载。

序号	毕业设计全套资源（点击下载）
本项目源码	基于C++的RSA文件加密软件的设计与实现（源码+文档）_java_RSA_文件加密.zip