ahut 周赛3
A.gzm判试卷
AhutOj
线段树(注意,一定要开到4*N,不然会RE)
单点更新(求区间最值)
单点更新不需要懒标记,区间修改是大量的点,需要懒标记
AC代码:
#include
#include
#include
#include
using namespace std;
#define int long long
#define endl '\n'
const int N=8e5+10,INF=2e9;
int a[N];
int tr[N];
int n,m;
void build(int id,int l,int r){
if(l==r) {
tr[id]=a[l];
return;
}
int mid=(l+r)/2;
build(id*2,l,mid);
build(id*2+1,mid+1,r);
tr[id]=max(tr[id*2],tr[id*2+1]);
}
void point_update(int id,int l,int r,int x,int v){
if(l==r){
tr[id]=v;
return;
}
int mid=(l+r)/2;
if(x<=mid) point_update(id*2,l,mid,x,v);
else point_update(id*2+1,mid+1,r,x,v);
tr[id]=max(tr[id*2],tr[id*2+1]);
}
int find(int id,int l,int r,int x,int y){
if(x<=l&&r<=y) return tr[id];
int mid=(l+r)/2,ans=-INF;
if(x<=mid) ans=max(ans,find(id*2,l,mid,x,y));
if(y>mid) ans=max(ans,find(id*2+1,mid+1,r,x,y));
return ans;
}
void solve()
{
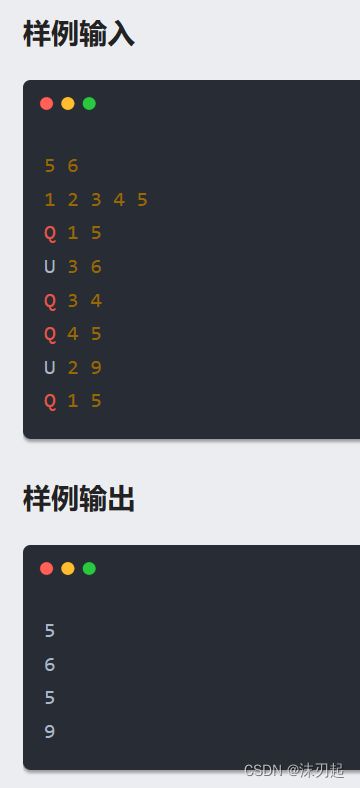
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--){
char op;
int x,y;
cin>>op>>x>>y;
if(op=='U') point_update(1,1,n,x,y);
else if(op=='Q') cout< B.gzm的新栈
AhutOj
Push和Pop就正常操作
然后对于Onethird操作,使用树状数组+二分
用树状数组,sum(x)表示从1到x一共有多少个数,然后使用二分答案,精确找到x,使得sum(x)==(n+2)/3
如果第(n+2)/3个数,和它相同的数只有一个的话,那么可以找到x使得sum(x)刚好等于(n+2)/3
但是如果和它相同的数不止一个,那么找到的x,sum(x)会大于(n+2)/3,则r=mid.并且sum(x-1)
用了ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);就不能用scanf,printf以及puts了
AC代码(stl版的栈):
#include
#include
#include
#include
//#define int long long
#define endl '\n'
using namespace std;
const int N=1e5+10;
int tr[N];
int stk[N];
int tt;
int lowbit(int x){
return x & -x;
}
void add(int x,int c){
for(int i=x;i<=N;i+=lowbit(i)) tr[i]+=c;
}
int sum(int x){
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=tr[i];
return res;
}
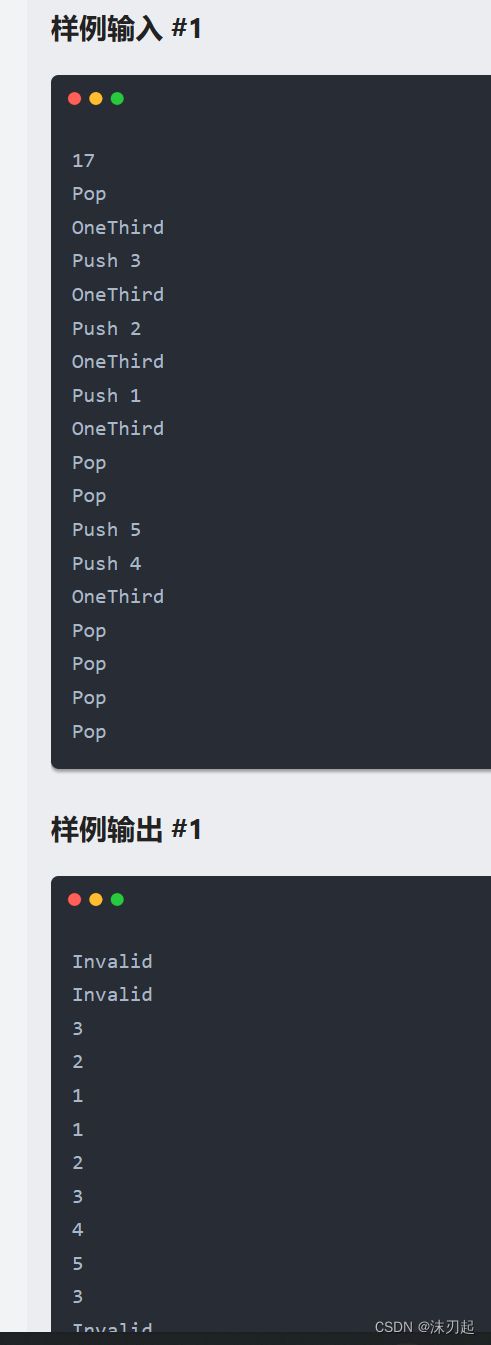
void solve()
{
int m;
cin>>m;
stacks;
int n=0;
while(m--){
string op;
cin>>op;
if(op=="Pop"){
if(s.empty()){
puts("Invalid");
continue;
}
cout<>x;
add(x,1);
s.push(x);
n++;
}
else{
if(s.empty()){
puts("Invalid");
continue;
}
int l=1,r=N;
while(l=(n+2)/3) r=mid;
else l=mid+1;
}
cout< AC代码(数组模拟栈):
#include
#include
#include
#include
//#define int long long
#define endl '\n'
using namespace std;
const int N=1e5+10;
int tr[N];
int stk[N];
int tt;
int lowbit(int x){
return x & -x;
}
void add(int x,int c){
for(int i=x;i<=N;i+=lowbit(i)) tr[i]+=c;
}
int sum(int x){
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=tr[i];
return res;
}
void solve()
{
int m;
cin>>m;
while(m--){
string op;
cin>>op;
if(op=="Pop"){
if(!tt){
puts("Invalid");
continue;
}
cout<>stk[tt];
add(stk[tt],1);
}
else{
if(!tt){
puts("Invalid");
continue;
}
int n=tt;
int l=1,r=N;
while(l=(n+2)/3) r=mid;
else l=mid+1;
}
cout< C.gzm的新栈
AhutOj
数最大为1000000000,第二大为999999999,所有位数加起来为81,再加起来为9,已经变成个位数了,再怎么加都不变了,所以[1,1e9]中的任何一个数只需要最多两次就可以变成个位数,再怎么操作都不会变了,该下标就不用再操作了
利用并查集,当a[x]变为个位数时,p[x]就指向x+1,当下次再到该x时,就利用find(x)找到x的祖宗,跳过之间已经不需要操作的下标
注意,p[n+1]要初始化为n+1,否则p[n+1]一开始为0的话,当调用find(n)时,p[n]=n+1,再调用find(n+1),然后n+1不等于0,这样的话,就一直递归不出来,导致死循环
AC代码:
#include
#include
#include
#define endl '\n'
using namespace std;
const int N=2e5+10;
int a[N];
int p[N];
int n,q;
void init(){
for(int i=1;i<=n+1;i++) p[i]=i;
}
//并查集
int find(int x) {
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
//求a[x]所有位数之和,并返回给a[x]
void sum(int x){
int ans=0;
while(a[x]){
ans+=a[x]%10;
a[x]/=10;
}
a[x]=ans;
}
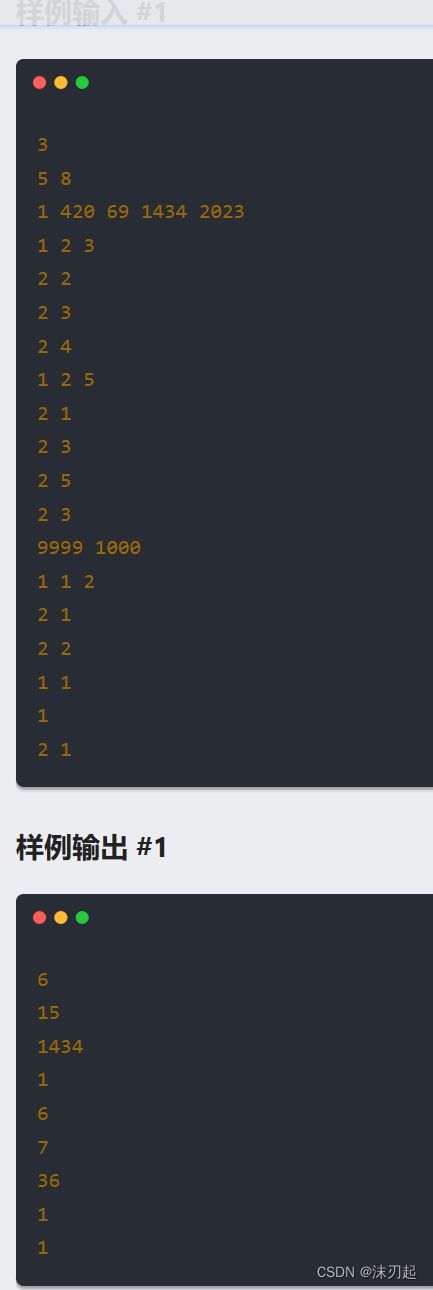
void solve()
{
cin>>n>>q;
init();
for(int i=1;i<=n;i++) cin>>a[i];
while(q--){
int op;
cin>>op;
if(op==1){
int l,r;
cin>>l>>r;
while(l<=r){
sum(l);
if(a[l]<10) p[l]=l+1;
l++;
l=find(l);
}
}
else{
int x;
cin>>x;
cout<>t;
while(t--)
solve();
return 0;
} D.gzm的旋转图腾
AhutOj
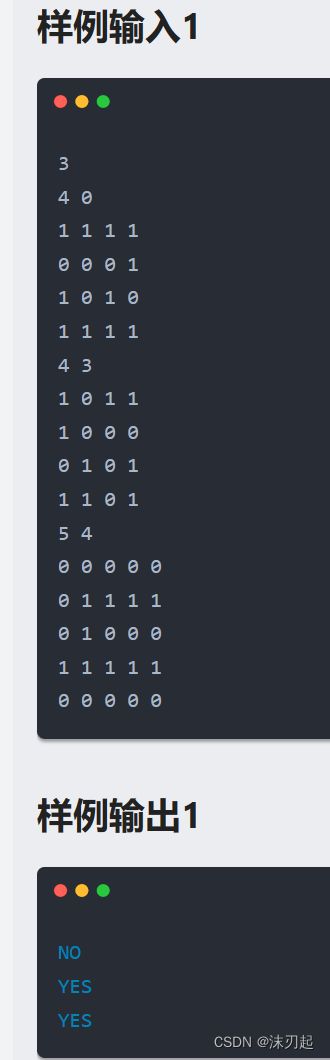
题目表达的意思不是很明确,有一些歧义,题目的意思是能否通过恰好k次操作(0变1或1变0),使得该图形旋转180度之后和原本一样(也就是中心对称)
首先要考虑特殊情况,这是做题目最应优先考虑的:当n等于1时,直接输出YES
遍历一遍矩阵,数一下有多少对点不是中心对称,记为cnt,如果cnt超过了题目的限制k,那么就直接输出NO
如果cnt小于k,还不一定是NO.
当n为奇数时,最中心的那个点始终中心对称,我们可以变换最中心的点,01交替变换,直至次数刚好为k
当n为偶数时,我们可以将一对中心对称的相同的点同时从1变为0或从0变为1,故如果k-cnt是2的倍数,就输出YES,否则输出NO
AC代码:
#include
#include
#include
#include
#include
#include
using namespace std;
const int N=1010;
int a[N][N];
//int tmp[N][N];
int n,k;
旋转180度
//void rotate(int a[N][N])
//{
// memset(tmp,0,sizeof tmp);
// for(int i=0;i>n>>k;
for(int i=0;i>a[i][j];
}
}
if(n==1){
puts("YES");
return;
}
int cnt=0;
for(int i=0;ik){
puts("NO");
return;
}
}
}
}
if(n%2==1) puts("YES");
else{
if((cnt-k)%2==0) puts("YES");
else puts("NO");
}
}
int main()
{
int t;
cin>>t;
while(t--)
solve();
return 0;
} E.gzm学线段树
AhutOj
线段树(注意,一定要开到4*N,不然会RE)
区间修改(求区间最值)
需要懒标记
AC代码:
#include
#include
#include
#include
using namespace std;
#define int long long
#define endl '\n'
const int N=8e5+10,INF=2e9;
int a[N];
int lazy[N];
int sum[N];
int n,m;
void build(int id,int l,int r){
if(l==r){
sum[id]=a[l];
return;
}
int mid=(l+r)/2;
build(id*2,l,mid);
build(id*2+1,mid+1,r);
sum[id]=sum[id*2]+sum[id*2+1];
}
void push_up(int id){
sum[id]=sum[id*2]+sum[id*2+1];
}
void push_down(int id,int l,int r){
if(lazy[id]){
int mid=(l+r)/2;
lazy[id*2]+=lazy[id];
lazy[id*2+1]+=lazy[id];
sum[id*2]+=lazy[id]*(mid-l+1);
sum[id*2+1]+=lazy[id]*(r-mid);
lazy[id]=0;
}
}
void range_update(int id,int l,int r,int x,int y,int v){
if(x<=l&&r<=y){
lazy[id]+=v;
sum[id]+=v*(r-l+1);
return;
}
push_down(id,l,r);
int mid=(l+r)/2;
if(x<=mid) range_update(id*2,l,mid,x,y,v);
if(y>mid) range_update(id*2+1,mid+1,r,x,y,v);
push_up(id);
}
int find(int id,int l,int r,int x,int y){
if(x<=l&&r<=y) return sum[id];
push_down(id,l,r);
int mid=(l+r)/2,ans=0;
if(x<=mid) ans+=find(id*2,l,mid,x,y);
if(y>mid) ans+=find(id*2+1,mid+1,r,x,y);
return ans;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--){
char op;
cin>>op;
if(op=='C'){
int x,y,v;
cin>>x>>y>>v;
range_update(1,1,n,x,y,v);
}
else if(op=='Q'){
int x,y;
cin>>x>>y;
cout< F.gzm的新启发式可持久化线段树维护多重背包
AhutOj
思维题
对于正数来说,肯定乘的i越小越好,而我们完全可以做到让所有的正数都乘1,只需要从前往后一个一个删即可
但是对于负数,我们肯定要乘的i尽可能大,所以从后往前删,负数都是乘以它们本身的下标
故只需要将正数全部相加,负数则乘以它本身的下标再相加
AC代码:
#include
#include
#include
#include
#define int long long
using namespace std;
const int N=1e6+10;
int a[N];
void solve()
{
int n;
cin>>n;
int res=0;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
if(a[i]>0) res+=a[i];
else if(a[i]<0) res+=a[i]*i;
}
cout<