滤波算法——均值滤波，中值滤波，一阶(αβ)滤波，卡尔曼滤波

滤波算法——均值滤波，中值滤波，一阶(αβ)滤波，卡尔曼滤波

因工作涉及到数据滤波(滤噪)处理，汇总了一些网上简单的滤波算法，方便日后查看。

滤波算法包括：均值滤波，中值滤波，一阶(αβ)滤波，卡尔曼滤波。

本文主要是处理线性数据y=ax+b，对于非线性数据，简单的滤波算法效果有限。滤波算法都有自己的局限，针对不同问题需要选择合适的方法。

以下使用python实现简单demo，主要是方便画图。

为了方便，本文使用jupyter notebook直接导出markdown生成。

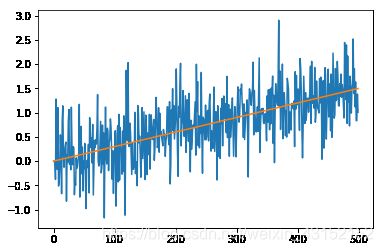
建立测试数据

真值y = 0.003*x
观测值加上随机白噪声

import random
import math
import numpy as np
import matplotlib.pyplot as plt

n = 500
real = [] # 真值
mear = [] # 观测值
pred = [] # 滤波值

# 建立真值和观测值
for i in range(n):
  num = 0.003 * i 
  real.append(num)
  num += 0.1 * np.random.standard_normal()  # 本身的不确定性
  num += 0.5 * np.random.standard_normal()  # 观测的不确定性
  mear.append(num)
  
plt.plot(range(n), mear)
plt.plot(range(n), real)
plt.show()

均值滤波

均值滤波是典型的线性滤波算法，在图像中应用比较多，原理是以该像素点周围的八个像素点取平均操作，然后替代该像素点，也就是卷积操作。对于处理简单的线性数据y=ax+b，原理也是类似的，取该点周围的n个点取平均即可，n可以看为是一个滑窗。因此，可以取该点的前后n个数据的平均值，也可以取前n个数据的平均值，根据不同场景数据设计即可。
如下代码比较适合离线数据处理，是对原始观测的数据中取某点的前后滑窗大小的均值，好比图像中应用中就是对原始图片滤波。如果对于在线数据，一个不断增加数据的数组，建议使用一阶滤波器或者kalman滤波器。

# window滑窗越大，滤波效果越明显，结果越滞后
# 设置了该点的左右滑窗大小，可根据实际情况选取参数
def average_filter(window_left, window_right, arr):
  size = len(arr)
  result = []
  for i in range(window_left, size-window_right):
    sum = 0
    # 滑窗
    for j in range(-window_left, window_right+1):
      sum += arr[i+j]
    sum /= (window_left + window_right + 1)
    result.append(sum)
  return result

pred = [] # 滤波值

# 前后5个，总共11个点求平均值
pred = average_filter(5, 5, mear)

# 前5个数，总共6个点求平均值
# pred = average_filter(5, 0, mear)


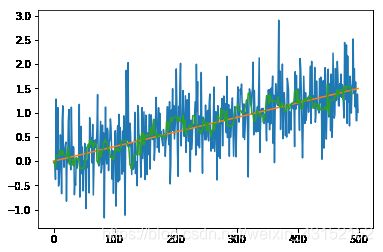
plt.plot(range(n), mear)
plt.plot(range(n), real)
# 会牺牲掉前后window大小的数据，可以作相应改进
plt.plot(range(len(pred)), pred)
print(len(pred))

490

中值滤波

和均值滤波相似，同样是选取固定大小滑窗，然后选取滑窗内的中位数作为滤波结果。或者选取中位数平均数，类似比赛中去掉最高最低分，对其余比分求平均，这种可以叫做中位值平均滤波法。思路都是差不多的，都是需要做一遍排序。
中值滤波能有效克服偶然因素引起的波动噪声。

# window滑窗越大，滤波效果越明显，结果越滞后
# 设置了该点的左右滑窗大小，可根据实际情况选取参数
def Median_Filter(window_left, window_right, arr):
  size = len(arr)
  result = []
  for i in range(window_left, size-window_right):
    # 滑窗
    temp = []
    for j in range(-window_left, window_right+1):
      temp.append(arr[i+j])
    temp.sort()
    point = temp[(int)(len(temp)/2)]
    result.append(point)
  return result

# 中值平均值滤波
def MedianAvg_Filter(window_left, window_right, arr):
  size = len(arr)
  result = []
  for i in range(window_left, size-window_right):
    # 滑窗
    temp = []
    for j in range(-window_left, window_right+1):
      temp.append(arr[i+j])
    temp.sort()
    # 可以去掉最大值后，取中位数的平均值
    median_mean = []
    for m in range(1, len(temp)-1):
      median_mean.append(temp[m])

    result.append(np.mean(median_mean))
  return result

pred = [] # 滤波值
# 前后5个，总共11个点求中值
pred = Median_Filter(5, 5, mear)
# pred = MedianAvg_Filter(5, 5, mear)

# 前5个数，总共6个点求中值
# pred = Median_filter(5, 0, mear)


plt.plot(range(n), mear)
plt.plot(range(n), real)
# 会牺牲掉前后window大小的数据，可以作相应改进
plt.plot(range(len(pred)), pred)

[]

一阶(αβ)滤波

一阶滤波是比较常用简单的滤波方法，就是当前采样结果和上一个滤波结果加权求和，权重和为1。对周期干扰噪声有良好的抑制作用，但同样会产生相位滞后，权重是固定值也是其缺点之一。

# a值越小，越不相信观测，滤波效果越明显，结果越滞后
def ab_filter(a, now):
  global last
  return a * now + (1 - a) * last

pred = []
last = mear[0]
pred.append(last)

for i in range(1, n):
  last = ab_filter(0.4, mear[i])
  pred.append(last)

plt.plot(range(n), mear)
plt.plot(range(n), real)
plt.plot(range(n), pred)

[]

卡尔曼滤波

关于卡尔曼滤波器的原理这里就不多做介绍了，可以查看我之前的文章卡尔曼滤波算法原理(KF,EKF,AKF,UKF)。
因为之前都是用kf处理带有运动模型的运动目标数据，一时还没有反应过来可以用它来处理简单的二维线性数据，惭愧。

# 滤波效果主要调整参数：
# 过程噪声方差q(越小越相信预测，反之亦然)， 观测噪声方差r(越小越相信观测，反之亦然)
q, r = 0.1, 2
# 状态均值x， 过程噪声均值w，方差p
x, w, p = 0, 0, 0
def kalman_filter(z):
  global x, p
  # 预测
  x_ = x + w
  p_ = p + q
  k = p_ / (p_ + r)
  # 更新
  x = x_ + k * (z - x_)
  p = (1-k) * p_
  return x

pred = [] # 滤波值
for i in range(n):
  pred.append(kalman_filter(mear[i]))
  
plt.plot(range(n), mear)
plt.plot(range(n), real)
plt.plot(range(n), pred)

[]

总结

以上对简单的线性数据处理完之后，就可以使用最小二乘法来拟合出一个比较好的结果，关于最小二乘法可以查看我之前的文章最小二乘法拟合线条的C++实现
因各个滤波器取的参数不一，结果对比起来没有意义，而且因为采样点比较多，没有具体分析细节，建议应用时测试充分选取合适的方法。
水平有限，有错误的地方希望大佬多加指正!

参考文章

1. 无人驾驶基本功专栏
2. 卡尔曼滤波器的深入理解与可视化
3. 中位值滤波
4. C#/.NET 波形滤波——中位值平均滤波法(防脉冲干扰平均滤波法)