java习题3
292. Nim 游戏
难度简单
你和你的朋友,两个人一起玩 Nim 游戏:
- 桌子上有一堆石头。
- 你们轮流进行自己的回合, 你作为先手 。
- 每一回合,轮到的人拿掉 1 - 3 块石头。
- 拿掉最后一块石头的人就是获胜者。
假设你们每一步都是最优解。请编写一个函数,来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢,返回 true;否则,返回 false 。
示例 1:
输入:n = 4
输出:false
解释:以下是可能的结果:
1. 移除1颗石头。你的朋友移走了3块石头,包括最后一块。你的朋友赢了。
2. 移除2个石子。你的朋友移走2块石头,包括最后一块。你的朋友赢了。
3.你移走3颗石子。你的朋友移走了最后一块石头。你的朋友赢了。
在所有结果中,你的朋友是赢家。
示例 2:
输入:n = 1 输出:true
示例 3:
输入:n = 2 输出:true
class Solution {
public boolean canWinNim(int n) {
return n%4==0?false:true;
}
}70. 爬楼梯
难度简单
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
class Solution {
public int climbStairs(int n) {
int arr[]=new int [n+1];
arr[0]=1;
arr[1]=1;
for(int i=2;i<=n;i++){
arr[i]=arr[i-1]+arr[i-2];
}
return arr[n];
}
}605. 种花问题
难度简单
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false 。
示例 1:
输入:flowerbed = [1,0,0,0,1], n = 1 输出:true
示例 2:
输入:flowerbed = [1,0,0,0,1], n = 2 输出:false
提示:
1 <= flowerbed.length <= 2 * 104flowerbed[i]为0或1flowerbed中不存在相邻的两朵花0 <= n <= flowerbed.length
class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
for (int i = 0; i < flowerbed.length; i++) {
if(flowerbed[i]==0&&(i+1==flowerbed.length||flowerbed[i+1]==0)){
n--;
i++;
}
else if(flowerbed[i]==1){
i++;
}
}
return n<=0;
}
}
217. 存在重复元素
难度简单
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1] 输出:true
示例 2:
输入:nums = [1,2,3,4] 输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2] 输出:true
提示:
1 <= nums.length <= 105-109 <= nums[i] <= 109
因为Set集合是不重复的,我们就可以使用set集合来实现去重,如果add()方法返回的是false,则说明这个元素重复出现过
class Solution {
public boolean containsDuplicate(int[] nums) {
HashSet count = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if(!count.add(nums[i]))
return true;
}
return false;
}
} 1217. 玩筹码
难度简单
有 n 个筹码。第 i 个筹码的位置是 position[i] 。
我们需要把所有筹码移到同一个位置。在一步中,我们可以将第 i 个筹码的位置从 position[i] 改变为:
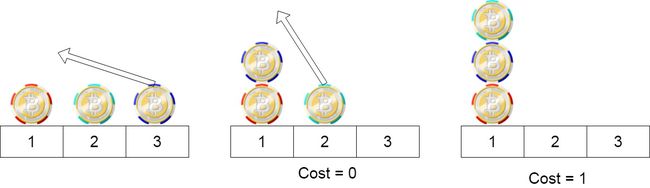
position[i] + 2或position[i] - 2,此时cost = 0position[i] + 1或position[i] - 1,此时cost = 1
返回将所有筹码移动到同一位置上所需要的 最小代价 。
示例 1:
输入:position = [1,2,3] 输出:1 解释:第一步:将位置3的筹码移动到位置1,成本为0。 第二步:将位置2的筹码移动到位置1,成本= 1。 总成本是1。
示例 2:
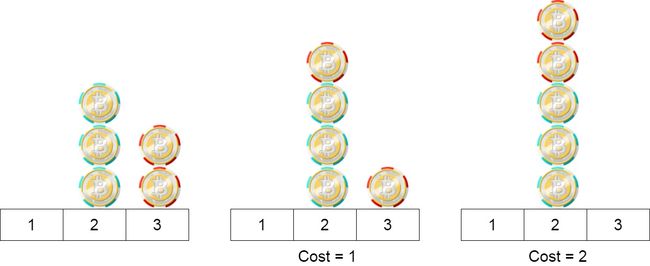
输入:position = [2,2,2,3,3] 输出:2 解释:我们可以把位置3的两个筹码移到位置2。每一步的成本为1。总成本= 2。
示例 3:
输入:position = [1,1000000000] 输出:1
提示:
1 <= position.length <= 1001 <= position[i] <= 10^9
这个题其实不用去模拟,其实题目意思就是要将全部的筹码移动到一个位置上,题目上说明
position[i] + 2或position[i] - 2,此时cost = 0
意思就是像个两个的不用步数,也就是说奇数看作是一起的,偶数看作是一起的
class Solution {
public int minCostToMoveChips(int[] position) {
int a=0,b=0;
for(int i=0;i268. 丢失的数字
难度简单
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1] 输出:2 解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1] 输出:2 解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1] 输出:8 解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0] 输出:1 解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
提示:
n == nums.length1 <= n <= 1040 <= nums[i] <= nnums中的所有数字都 独一无二
因为题目说了数据是独一无二的,我们就可以考虑使用HashSet集合来去重,先将元素添加到集合中,再去看集合中少了哪一个元素
class Solution {
public int missingNumber(int[] nums) {
HashSet arr = new HashSet<>();
for(int i=0;i 55. 跳跃游戏
难度中等
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 3 * 1040 <= nums[i] <= 105
这个题说的是是否可以跳到最后一个下标,我们只需要遍历一遍数组,不断更新可以跳到的位置,
如果此时i>maxJump就是不可以跳到,返回false
class Solution {
public boolean canJump(int[] nums) {
int maxJump=0;
for (int i=0;imaxJump){
return false;
}
maxJump=Math.max(maxJump,i+nums[i]);
}
return true;
}
} 121. 买卖股票的最佳时机
难度简单
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
这个题使用DP来做的话会快很多,
第一天就是prices[1],
第二就是dp[1]=Math.max(nums[0],nums[1]);
从第三天开始,就产生了两种选择要么是选第二天的,要么就选择第一天的和当前天数的
dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]);
class Solution {
public int maxProfit(int[] prices) {
int []dp=new int[prices.length];
dp[0]=prices[0];
int ans=0;
for(int i=1;ians?(prices[i]-dp[i]):ans;
}
return ans;
}
} 198. 打家劫舍
难度中等
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
class Solution {
public int rob(int[] nums) {
if(nums.length==1)
return nums[0];
int []dp=new int[nums.length];
dp[0]=nums[0];
dp[1]=Math.max(nums[0],nums[1]);
for(int i=2;i120. 三角形最小路径和
难度中等
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] 输出:11 解释:如下面简图所示: 2 3 4 6 5 7 4 1 8 3 自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]] 输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
这个题采用的是从下玩上来的得到答案,这样的话,当前的dp[i][j]就是,dp[i][j]=Math.min(dp[i+1][j],dp[i+1][j+1])+triangle.get(i).get(j);
class Solution {
public int minimumTotal(List> triangle) {
int n=triangle.size();
int [][]dp=new int[n+1][n+1];
for(int i=n-1;i>=0;i--){
for(int j=triangle.get(i).size()-1;j>=0;j--){
dp[i][j]=Math.min(dp[i+1][j],dp[i+1][j+1])+triangle.get(i).get(j);
}
}
return dp[0][0];
}
}