数据结构真题
数据结构真题
1. A. Bills of Paradise
- 线段树+并查集
- 四个操作:
- D x。标记大于等于 x 的第一个未标记的 a i a_i ai;若没有,则不操作.
- F x。查询大于等于 x 的第一个未标记的 a i a_i ai;若没有,则输出 1 0 12 10^{12} 1012.
- R x。清除小于等于 x 的所有标记;若没有,则不操作。本操作次数不超过10次.
- C x。查询小于等于 x 的所有未标记数之和;若没有,则输出0.
- 我们先排序,这样子可以很快定位到x。
- 因为单点查询修改,都是大于等于x的第一个 a i a_i ai,因此我们可以用并查集往后连。p[i] 表示从 i 开始往后第一个未标记的结点的下标。一开始都是未标记的,所以是 p[i] = i。标记了 i 之后,unite(i, i + 1),把 i 开始的未标记下一个结点连到 p[i + 1] 上面。
- 至于 R, C 操作,区间操作用线段树。线段树一开始都是零,只保存标记的节点。每标记一个结点,就把对应的地方 += a[i]。线段树结点保留三个属性:l, r, sum.
- 易错点:
- 找下一个未标记节点的时候:pos = find(id),而不是 pos = find(id)
- query 函数一定要小心
if (r <= mid) return query(2 * u, l, r);,递归的时候不是query(2 * u, l, mid)! - 每个结尾千万不要忘记输出空格!
#include2. C. Caesar Cipher
-
给出一个长度为 n 的序列,接下来有 m 次操作,每次操作分为下列两种类型:
- 1 l r:区间 [ l , r ] 内的所有数都加 1 并对 65536 取模,也就是 i ∈ [ l , r ] ,有 a[ i ] =( a[ i ] + 1 ) % 65536
- 2 x y len:查询两段区间 [ x , x + len - 1 ] 和 [ y , y + len - 1 ] 内的序列是否相同
-
这个题确实有几个可圈可点的地方
- 首先,他让每个数增加到到 2 16 2^{16} 216 变为0,相当于又引入了一个模数。而之前的字符串哈希是自然溢出取模,然而 2 16 2^{16} 216 与 2 64 2^{64} 264 并不互质,因此这样子会错。字符串哈希不仅要保证 base 和 mod 互质,还要保证取模的数也要互质。
- 这道题用字符串哈希第二种方法最简单,即 c 1 p + c 2 p 2 + . . . + c m p m c_1p+c_2p^{2}+...+c_mp^m c1p+c2p2+...+cmpm 表示字符串的哈希值。
- 小心三个地方,第一个是modify的时候小心,在要修改完整;第二个是取模的时候,出现减法,一定要 + mod 再 % mod,防止出现负数;第三个是,字符串哈希,对一段区间加上某一个数时,是加 base 幂的区间和 s u m p [ r ] − s u m p [ l − 1 ] sump[r] - sump[l-1] sump[r]−sump[l−1],而不是 p [ r ] − p [ l − 1 ] p[r] - p[l - 1] p[r]−p[l−1].
#include3. B. Bin Packing Problem
- 题意:n个物品,第i个物品的容量是 a[i] ,有无限个箱子,每个箱子的容量是 c ,问按照一下两种放法,最少需要几个箱子。
第一种:每次都选择最前面的可以放在物品的箱子,若不存在就增加一个箱子。
第二种:每次都选择剩余容量最小的且可以容纳物品的箱子,若不存在就增加一个箱子。
问两种方法各需要多少个箱子 - 第一个:是在数组中找到第一个大于等于x的数,这个用线段树,维护区间最大值,先一直往左找,找不到的话往右找。
- 第二种:找到一个动态有序序列中第一个大于等于x的数,平衡树嘛。不过,这个题用map就挺好的,需要记录重复的数据(虽然说map是红黑树但是这不重要)。
#include4. E. Easy DP Problem
- 题意:给你这么一个dp的方程,然后给出 l, r, k。即选择 a[l ~ r] 作为 b 数组,问 d p ( r − l + 1 , k ) dp(r - l + 1, k) dp(r−l+1,k) 这个数是多少。

- 多输入几个无序的序列,然后分析分析,可以看出来,题目问的是, ∑ i = 1 m i 2 \sum\limits_{i=1}^mi^2 i=1∑mi2 加上 a[l ~ r + 1] 这些数中的前 k 个大的数。这就需要主席树了。感觉省赛题确实比CCPC区域赛在思维上要简单一点。
#include4. I. Incredible photography
- 题意:给你一段序列,以某点为起点,你的移动规则是找到一个你能看到的高度严格大于你的点,然后你可以移动到那个点,之后又可以以相同的规则进行移动。求出以每个点为起点时能移动的最长距离。
- 很显然是单调栈+拓扑图最长路径。但是有一个关键的问题,就是这个找的是每个数向左看,和比他大的数第一个数相等的,且距离离他最远数。那么这个其实很简单,就是在维护单调栈的时候,如果出现
a[stk[tt]] == a[i]的情况,就把这个 stk[tt] 记录下来。后面往单调栈里面推入数字的时候,不推入 i 而推入 stk[tt]。这样子,就算出现 5 3 5 5 3 5 这样子的东西,就算中间数字不是连续的,也是可以正确的找到离他最远的符合要求的那个数字。
#include5. J. Just Another Game of Stones
- 吉老师线段树,复杂度是 O ( n log 2 n ) . O(n\log^2 n). O(nlog2n).
- 吉司机线段树主要是用来解决序列区间上满足部分满足一定性质的修改操作的,比方说把区间中小于x的数改成x,大于x的数改成x,甚至是区间取并和区间取或(实际上也就是区间中的每个数的每一位进行类似小于x改成x那种操作)下面主要说一下怎么处理区间中把小于x 的数改成x,其他的可以类比来做;
- 首先要记一个中间量,也就是次小值;然后再把线段树上每一个区间的最小值及其个数记录下来;
- 对于每次修改,设要和x进行对比;
- 如果当前找到的区间的最小值>=x,那么肯定没必要再往下处理了;
- 如果x>最小值但x<次小值(注意x严格小于次小值)那么只需要把最小值改成x,记录的最小值的数目都不需要改,这样线段树上维护的其他信息也可以很方便的修改(例如区间和一类的信息)
- 如果x>=次小值,那递归处理左右子区间再合并信息回来;
- 题意。有一个线段树,维护两个操作
- 1 l r:对于所有 i ∈ [ l , r ] i \in [l, r] i∈[l,r] 执行 a i = m a x ( a i , x ) a_i = max(a_i, x) ai=max(ai,x)
- 2 l r x:对于区间 [ l , r ] [l, r] [l,r] 内的 a i a_i ai 加上 x 这一共 r − l + 2 r - l + 2 r−l+2 个数进行尼姆游戏,问先手必胜的情况下第一次能有多少种不同的取石子方案。
- 根据尼姆游戏,我们知道,我们先把所有值取异或得到 res,然后记 res 最高位1是第 k 位,查一下有多少个 a i a_i ai 的第 k 位是1.
- 对于第一个操作。我们记录这个区间最小值、次小值、最小值的个数。那么,如果传进来的x >= 最小值,那么什么都不变;如果最小值 < x < 次小值,那么就把次小值变成 x,其他的不用变;如果 x >= 次小值,那么就递归处理两个儿子。
- 对于第二个操作,因为是取异或,且需要知道位的信息,所以我们对每一位维护一个信息。而该位异或的结果取决于该位的个数。
- 数组一定要开大一点,千万别吝惜。因为有时候会出现莫名其妙的错误。就比如这道题,把sum数组从30变成35后就不出现段错误了。
#includeJ题实际上是本场唯一的一个套路题,前半考察对nim游戏的基础理解,后半考察Segment Beats。我组题会偏向于在比赛中设置这么一个题目,可以说是给那些有准备的队伍一个糖果。而实际上我之所以选用Segment Beats就是因为在不久前ccpc网络赛中就出现过一个,可以理解为我在考察大家平时的补题情况。
6. I. Stock Analysis
- 给一个序列 ( n ≤ 2000 ) (n\le 2000) (n≤2000),给 Q ( Q ≤ 20000 ) Q(Q\le20000) Q(Q≤20000) 组询问 ( l , r , u ) (l, r, u) (l,r,u),问在 ( l , r ) (l, r) (l,r) 内,不大于 u u u 的最大连续子段和是多少?
- 一开始用线段树套平衡树,后来发现不对。因为树套树只能维护一段一段的区间。如果某个区间横跨线段树的维护的两个区间,答案也是横跨了结点的两个区间,这样的答案是查询不到的。
- 有一个思路是,所有区间和总共也只有 2e6 个。因此预处理出所有区间和,再读入所有询问。然后按照值排序。这样子的话,大于 U 的区间和只会在 U 之后出现,这样子的话,就可以转化为求小矩形最大值的问题。
- 但是,不会求小矩形最大值。
- 看不懂的二维树状数组写法
#include7. K. Kth Query
#include8. H. Sequence
- 动态维护一个序列(带修改),找到最小值为 a x a_x ax 的连续子序列的数量。
- 核心内容就是如何找到左边第一个比它小的数和右边第一个比它小的数。
- 以找到右边第一个比它小的数举例:
法一:
- 可以二分搜索,在 [x, N] 找到最小值是否小于x(线段树维护)。我们对查询的区间长度二分 (lb = 0, ub = N - x + 1). 如果当前长度找到比它小的数,就缩短查询区间长度;如果当前长度找到比它小的数,就扩大区间长度。
#include法二:
具体做法:只考虑求 a x a_x ax左边的值,右边类似
1.因为要尽量离 a x a_x ax近,那么贪心的检查右子树中是否含 x x x。有 并且 区间最小值 a x a_x ax 的话. 那么右边可能存在答案(1.2为什么说可能,因为可能存在 唯一 一个 v a l < a x val < a_x val<ax,其位置 > x > x >x. 这样答案就不存在,但是我们还是会往右子树走.)
2.如果右子树不符合要求,自然就往左子树看。若左子树最小值 < a x < a_x <ax. 那就往左子树搜索(这个时候答案是一定存在的).
根据:只要往左走,那么答案就一定存在。考虑其生成树的样子。要么是一直往右走。要么只能往左拐一下就直接找到答案。那么单次查询最差也就两条链。即 O ( 2 log n ) O(2\log n) O(2logn) 的复杂度.
————————————————
版权声明:本文为CSDN博主「Implicit_」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_35577488/article/details/109923150
#include9. E. Phone Network
- 题意:一个长度n的数组,每个数在[ 1,m ]区间内,保证了每个数(在[ 1 , m ])至少出现过一次。对于每个 i ∈ [ 1 , m ],分别输出在原数列中,包含了 [ 1 , i ] 的所有种类数字的最短区间长度。
- 别人的题解
#include
//因为last - mi[k] + 1 作为以 i 为左端点len,只能作为在 [pre, cnt] 的答案。
int find(int u, int l, int r, int last)
{
if(tr[u].mi >= last) return -1;
if(tr[u].l == tr[u].r) return tr[u].l;
pushdown(u);
int mid = (tr[u].l + tr[u].r) / 2;
int tmp = -1;
tmp = find(2 * u + 1, l, r, last);
if(tmp == -1 && l <= mid) tmp = find(2 * u, l, r, last);
return tmp;
}
int main()
{
scanf("%d%d", &N, &M);
for(int i = 1, x; i <= N; i++){
scanf("%d", &x);
w[x].push_back(i);
}
build(1, 1, N);
for(int i = 1; i <= M; i++){
int pre = 1, sz = w[i].size();
for(int j = 0; j < sz; j++){
int last = w[i][j];
int cnt = find(1, pre, last, last);
if(cnt != -1) modify(1, pre, cnt, last);
pre = last + 1;
}
if(w[i].back() + 1 <= N) modify(1, w[i].back() + 1, N, INF);
printf("%d ", tr[1].len);
}
return 0;
}
10. C. Data Structure Problem
- 题意:
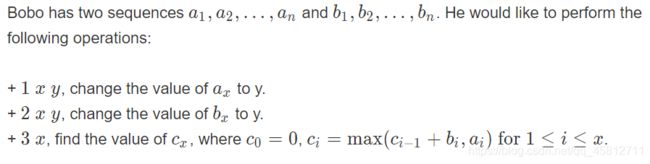
- 题解:

- 线段树维护b数组的区间和, a i − s i a_i - s_i ai−si 的最大值,以及懒标记(下面会解释)。
- 如果是第一个操作,那么就单点修改 a i − s i a_i - s_i ai−si 的值。
- 如果是第二个操作,先单点修改 b 数组的值(同时维护区间和的信息),然后从 x x x 到 N N N 区间每个 a i − s i a_i - s_i ai−si 都减去 b x b_x bx 增大的值。
- 第三个操作查询即可。即 s x + m a x ( 0 , m a x { a i − s i ∣ x ≤ i ≤ n } ) s_x + max(0, max\{a_i - s_i | x \le i \le n\}) sx+max(0,max{ai−si∣x≤i≤n}).
#include11. Problem - D - Codeforces
- 题意:

- 几个数的乘积等于他们的LCM,等价于这几个数字两两互质。
- 那么,我们可以看他们的每一个质因数,用 r [ i ] r[i] r[i] 表示 [ i , r [ i ] ) [i, r[i]) [i,r[i]) 之间所有数字两两互质。那么 i 开始的 r [ i ] r[i] r[i] 表示下一个区间的位置。
- 找 r [ i ] r[i] r[i] 可以这样子:找到所有 a [ i ] a[i] a[i] 的质因数,看看下一个质因数的位置在哪里,然后和 r [ i + 1 ] r[i + 1] r[i+1] 这些数中取一个最小值。
- 这样子,我们可以一直
u = r[r[r[i]]];。可以联想最近公共祖先。用树上倍增的方法快速寻找。 - 把这个 r [ i ] r[i] r[i] 想象成一个树,根节点在 n + 1 n+1 n+1,子节点向父节点连边。
#include