西瓜书课后题——第八章(集成学习)
8.1 证明式(8.3)
公式编辑起来比较麻烦,直接手写拍一个图片给出详细的证明过程。
8.2 证明:
首先,要知道0/1损失函数的一致替代函数的含义。因为0/1损失非凸、非连续,数学性质不好,为了便于计算求解,人们用一些数学性质比较好的函数来替代0/1损失函数。常用的替代函数有指数函数、对数函数、hinge函数。 可参见西瓜书130页的内容。
0/1损失函数原型如下:
所以,对于任意损失函数 ![]() , 则整体损失 Loss =
, 则整体损失 Loss = ![]()
当![]() 时,也就是 x 分类为1的概率更大时,为了保证损失函数较小,则希望
时,也就是 x 分类为1的概率更大时,为了保证损失函数较小,则希望![]() , 又因为题中说明 损失函数
, 又因为题中说明 损失函数 ![]() 对 H(x) 是单调递减的,则 由
对 H(x) 是单调递减的,则 由 ![]() 可知,
可知,![]() ,因为H(x)取值为 +1 和 -1, 所以此时 H(x) 只能为 1 ;
,因为H(x)取值为 +1 和 -1, 所以此时 H(x) 只能为 1 ;
同理,当 x 分类为 -1 的概率更大时,H(x) 取值即为 -1。
因此可得,在最小化由 l 损失函数计算得到的整体损失的过程中,已经达到了贝叶斯最优错误率。 可参见西瓜书174页 。 因此即可为0/1损失函数的替代函数。(个人的理解也就是说,最小化这个函数的过程,也就是在使预测的标签和实际真实标签尽最大可能一致的过程。)
8.3 AdaBoost集成编程实现。
该算法是序列化的串行的集成学习算法,算法的具体步骤见西瓜书 第174页,相关推导过程见 173~177页。此处不再详述。
基于西瓜数据集3.0alpha,采用决策树为基学习器,训练11轮得到最终结果。由于数据量比较小,所以采用的是决策数桩为基学习器。
采用最大信息增益作为划分属性选择的依据,在计算交叉熵时,相较于之前第四章中的做法,这里要计算加权的交叉熵。
另外需要注意一点就是错误率的计算也是要加权进行。 权重更新一定切记进行规范化操作!!
完整的代码如下:
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
class Adaboost:
# 导入数据
def loadData(self):
dataset = pd.read_excel('./WaterMelon_3.0.xlsx',encoding = 'gbk') # 读取数据
Attributes = dataset.columns # 所有属性的名称
m,n = np.shape(dataset) # 得到数据集大小
dataset = np.matrix(dataset)
for i in range(m): # 将标签替换成 好瓜 1 和 坏瓜 -1
if dataset[i,n-1]=='是': dataset[i,n-1] = 1
else : dataset[i,n-1] = -1
self.future = Attributes[1:n-1] # 特征名称(属性名称)
self.x = dataset[:,1:n-1] # 样本
self.y = dataset[:,n-1].flat # 实际标签
self.m = m # 样本个数
def __init__(self,T):
self.loadData()
self.T = T # 迭代次数
self.seg_future = list() # 存贮每一个基学习器用来划分的属性
self.seg_value = list() # 存贮每一个基学习器的分割点
self.flag = list() # 标志每一个基学习器的判断方向。
# 取0时 <= value 的样本标签为1,取1时 >value 的样本标签为1
self.w = 1.0/self.m * np.ones((self.m,)) # 初始的权重
# 计算交叉熵
def entropyD(self,D): # D 表示样本的编号,从0到16
pos = 0.0000000001
neg = 0.0000000001
for i in D:
if self.y[i]==1: pos = pos + self.w[i] # 标签为1的权重
else: neg = neg + self.w[i] # 标签为-1的权重
P_pos = pos/(pos+neg) # 标签为1占的比例
P_neg = neg/(pos+neg) # 标签为-1占的比例
ans = - P_pos * math.log2(P_pos) - P_neg * math.log2(P_neg) # 交叉熵
return ans
# 获得在连续属性上的最大信息增益及对应的划分点
def gainFloat(self,p): # p为对应属性编号(0表示密度,1表示含糖率)
a = []
for i in range(self.m): # 得到所有属性值
a.append(self.x[i,p])
a.sort() # 排序
T = []
for i in range(len(a)-1): # 计算每一个划分点
T.append(round((a[i]+a[i+1])/2,4))
res = self.entropyD([i for i in range(self.m)]) # 整体交叉熵
ans = 0
divideV = T[0]
for i in range(len(T)): # 循环根据每一个分割点进行划分
left = []
right = []
for j in range(self.m): # 根据特定分割点将样本分成两部分
if(self.x[j,p] <= T[i]):
left.append(j)
else:
right.append(j)
temp = res-self.entropyD(left)-self.entropyD(right) # 计算特定分割点下的信息增益
if temp>ans:
divideV = T[i] # 始终存贮产生最大信息增益的分割点
ans = temp # 存贮最大的信息增益
return ans,divideV
# 进行决策,选择合适的属性进行划分
def decision_tree(self):
gain_1,devide_1 = self.gainFloat(0) # 得到对应属性上的信息增益及划分点
gain_2,devide_2 = self.gainFloat(1)
if gain_1 >= gain_2: # 选择信息增益大的属性作为划分属性
self.seg_future.append(self.future[0])
self.seg_value.append(devide_1)
V = devide_1
p = 0
else:
self.seg_future.append(self.future[1])
self.seg_value.append(devide_2)
V = devide_2
p = 1
left_total = 0
right_total = 0
for i in range(self.m): # 计算划分之后每一部分的分类结果
if self.x[i,p] <= V:
left_total = left_total + self.y[i]*self.w[i] # 加权分类得分
else:
right_total = right_total + self.y[i]*self.w[i]
if left_total > right_total:
flagg = 0
else:
flagg = 1
self.flag.append(flagg) # flag表示着分类的情况
# 得到样本在当前基学习器上的预测
def pridect(self):
hlist = np.ones((self.m,))
if self.seg_future[-1]=='密度': p = 0
else: p = 1
if self.flag[-1]==0: # 此时小于等于V的样本预测为1
for i in range(self.m):
if self.x[i,p] <= self.seg_value[-1]:
hlist[i] = 1
else: hlist[i] = -1
else: # 此时大于V的样本预测是1
for i in range(self.m):
if self.x[i,p] <= self.seg_value[-1]:
hlist[i] = -1
else:
hlist[i] = 1
return hlist
# 计算当前基学习器分类的错误率
def getError(self,h):
error = 0
for i in range(self.m):
if self.y[i]!=h[i]:
error = error + self.w[i]
return error # 返回错误率
# 训练过程,进行集成
def train(self):
H = np.zeros(self.m)
self.H_predict = [] # 存贮每一个集成之后的分类结果
self.alpha = list() # 存贮基学习器的权重
for t in range(self.T):
self.decision_tree() # 得到基学习器分类结果
hlist = self.pridect() # 计算该基学习器的预测值
error = self.getError(hlist) # 计算该基学习器的错误率
if error > 0.5: break
alp = 0.5*np.log((1-error)/error) # 计算基学习器权重
H = np.add(H,alp*hlist) # 得到 t 个分类器集成后的分类结果(加权集成)
self.H_predict.append(np.sign(H))
self.alpha.append(alp)
for i in range(self.m):
self.w[i] = self.w[i]*np.exp(-self.y[i]*hlist[i]*alp) # 更新权重
self.w[i] = self.w[i]/self.w.sum() # 归泛化处理,保证权重之和为1
# 打印相关结果
def myPrint(self):
tplt_1 = "{0:<10}\t{1:<10}\t{2:<10}\t{3:<10}\t{4:<10}"
print(tplt_1.format('轮数','划分属性','划分点','何时取1?','学习器权重'))
for i in range(len(self.alpha)):
if self.flag[i]==0:
print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
'x <= V',str(self.alpha[i])))
else:
print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
'x > V',str(self.alpha[i])))
print()
print('------'*10)
print()
print('%-6s'%('集成个数'),end='')
self.print_2('样本',[i+1 for i in range(17)])
print()
print('%-6s'%('真实标签'),end='')
self.print_1(self.y)
print()
for num in range(self.T):
print('%-10s'%(str(num+1)),end='')
self.print_1(self.H_predict[num])
print()
def print_1(self,h):
for i in h:
print('%-10s'%(str(np.int(i))),end='')
def print_2(self,str1,h):
for i in h:
print('%-8s'%(str1+str(i)),end='')
# 绘图
def myPlot(self):
Rx = []
Ry = []
Bx = []
By = []
for i in range(self.m):
if self.y[i]==1:
Rx.append(self.x[i,0])
Ry.append(self.x[i,1])
else:
Bx.append(self.x[i,0])
By.append(self.x[i,1])
plt.figure(1)
l1, = plt.plot(Rx,Ry,'r+')
l2, = plt.plot(Bx,By,'b_')
plt.xlabel('密度')
plt.ylabel('含糖率')
plt.legend(handles=[l1,l2],labels=['好瓜','坏瓜'],loc='best')
for i in range(len(self.seg_value)):
if self.seg_future[i]=='密度':
plt.plot([self.seg_value[i],self.seg_value[i]],[0.01,0.5])
else:
plt.plot([0.2,0.8],[self.seg_value[i],self.seg_value[i]])
plt.show()
def main():
ada = Adaboost(11)
ada.train()
ada.myPrint()
ada.myPlot()
if __name__== '__main__':
main()
最终输出打印的结果如下所示:
轮数 划分属性 划分点 何时取1? 学习器权重
0 含糖率 0.126 x > V 0.589327498171
1 含糖率 0.373 x > V 0.706451630048
2 密度 0.3815 x > V 0.817530731077
3 含糖率 0.373 x > V 0.774626608326
4 密度 0.6365 x <= V 1.4597062855
5 含糖率 0.373 x > V 1.16724429733
6 含糖率 0.126 x > V 1.6377001605
7 含糖率 0.373 x > V 1.42032462978
8 密度 0.3815 x > V 1.6358239935
9 含糖率 0.373 x > V 1.53370208033
10 密度 0.6365 x <= V 2.95664223935
------------------------------------------------------------
集成个数 样本1 样本2 样本3 样本4 样本5 样本6 样本7 样本8 样本9 样本10 样本11 样本12 样本13 样本14 样本15 样本16 样本17
真实标签 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
1 1 1 1 1 1 1 1 1 -1 1 -1 -1 1 1 1 -1 -1
2 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
3 1 1 1 1 1 1 1 1 -1 -1 -1 -1 1 1 -1 -1 -1
4 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
5 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 1 -1
6 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
7 1 1 1 1 1 1 1 1 -1 1 -1 -1 -1 -1 1 -1 -1
8 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
9 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
10 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
11 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
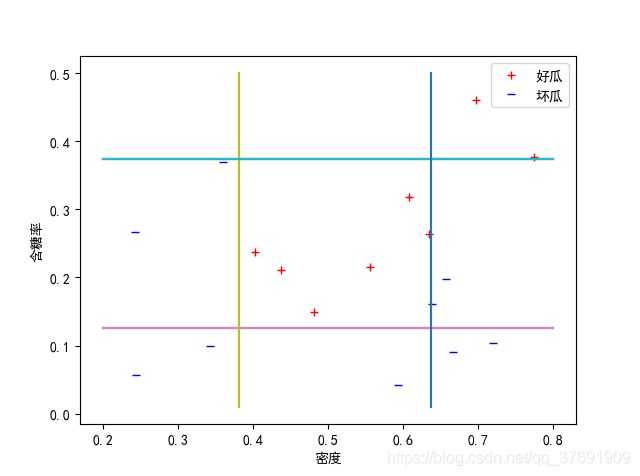
可以看出,在集成的基学习器个数达到8之后,已经可以将样本全部正确分类。
得到的分类图如下:
可见,已经可以将好瓜和坏瓜分开。
但是,疑惑的一点是得到的结果和书上的结果不太一样,检查程序也没有发现哪里出现了偏差,而且这个程序最后集成的结果也实现了完全正确的划分。所以如果各位知道哪里出现了问题,还请不吝赐教!!
8.4 GradientBoosting 和 AdaBoost 的异同
首先,这两种算法都属于 Boosting 算法,思想就是以某种方式在每一个基学习器的训练过程中更加关注在上一轮中训练错误的样本;都是个体学习器之间存在强依赖关系、必须串行生成的序列化方法;均可以将弱学习器提升为强学习器;主要关注于降低偏差,因此可以基于泛化能力非常弱的学习器得出很强的集成。
不同之处在于:AdaBoost 主要是通过增加在上一轮中训练错误样本的权重来达到关注预测错误样本的目的。 而 GradientBoosting 是用负梯度来作为上一轮中基学习器犯错的衡量指标,从而在下一轮中通过拟合上一轮中的负梯度来达到纠正上一轮中所犯错误的目的。 这个思想的理论依据就是 函数空间的梯度下降 。
关于 AdaBoost 和 GradientBoosting 更进一步的原理和算法实现可以参考这些博文:https://www.cnblogs.com/massquantity/p/9174746.html
8.5 编程实现Bagging。
该算法是一个并行的集成学习算法,根据书上算法的描述,首先要进行自助采样,从原始样本集中有放回地选取和初始样本集大小相同的一批样本,然后在抽取的样本上学习得到一个分类器。重复这个过程,得到多个分类器,最终通过简单投票法进行决策。
在自助采样的时候,本人认为既然是有放回地随机抽取,则应该使用均匀分布来产生随机数更准确,而不宜使用正态分布。因此,在最初进行编程时,我的思路是完全按照书上算法的描述使用自助采样抽取样本,抽取的每一个样本权重都一样(也就是样本不带权值),得到的采样样本集里面可能包含多个相同样本,也必然缺少某些样本值。 之后,单纯地使用这个抽取的样本集进行交叉熵、信息增益等的计算,实现决策树分类,得到一个学习器。 然后使用这个学习器在最初始的样本上进行测试。最终用简单投票法实现集成。
具体代码如下:
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
class Bagging:
# 导入数据
def loadData(self):
dataset = pd.read_excel('./WaterMelon_3.0.xlsx',encoding = 'gbk') # 读取数据
Attributes = dataset.columns # 所有属性的名称
m,n = np.shape(dataset) # 得到数据集大小
dataset = np.matrix(dataset)
for i in range(m): # 将标签替换成 好瓜 1 和 坏瓜 -1
if dataset[i,n-1]=='是': dataset[i,n-1] = 1
else : dataset[i,n-1] = -1
self.future = Attributes[1:n-1] # 特征名称(属性名称)
self.x = dataset[:,1:n-1] # 样本
self.y = dataset[:,n-1].flat # 实际标签
self.m = m # 样本个数
def __init__(self,T):
self.loadData()
self.T = T # 迭代次数
self.seg_future = list() # 存贮每一个基学习器用来划分的属性
self.seg_value = list() # 存贮每一个基学习器的分割点
self.flag = list() # 标志每一个基学习器的判断方向。
# 取0时 <= value 的样本标签为1,取1时 >value 的样本标签为1
# 自助采样
def boostStrap(self):
b = []
for i in range(self.m):
b.append(int(np.floor(np.random.uniform(0,17))))
X = [0,0]
Y = []
for i in range(self.m):
X = np.vstack((X,self.x[b[i],:]))
Y.append(self.y[b[i]])
print(X[1:,:])
print(np.shape(X))
return X[1:,:],Y,b
# 计算交叉熵
def entropyD(self,D): # D 表示样本的编号,从0到16
pos = 0.0000000001
neg = 0.0000000001
for i in D:
if self.y[i]==1: pos = pos + 1 # 标签为1的权重
else: neg = neg + 1 # 标签为-1的权重
P_pos = pos/(pos+neg) # 标签为1占的比例
P_neg = neg/(pos+neg) # 标签为-1占的比例
ans = - P_pos * math.log2(P_pos) - P_neg * math.log2(P_neg) # 交叉熵
return ans
# 获得在连续属性上的最大信息增益及对应的划分点
def gainFloat(self,p,X,b): # p为对应属性编号(0表示密度,1表示含糖率)
# b 是对应样本的真实编号
a = [] # X为经过自助采样后得到的样本集
for i in range(self.m): # 得到所有属性值
a.append(X[i,p])
a.sort() # 排序
T = []
for i in range(len(a)-1): # 计算每一个划分点
T.append(round((a[i]+a[i+1])/2,4)) # 保留四位小数
res = self.entropyD(b) # 样本整体交叉熵
ans = 0
divideV = T[0]
for i in range(len(T)): # 循环根据每一个分割点进行划分
left = []
right = []
for j in range(self.m): # 根据特定分割点将样本分成两部分
if(self.x[j,p] <= T[i]):
left.append(b[j])
else:
right.append(b[j])
temp = res-self.entropyD(left)-self.entropyD(right) # 计算特定分割点下的信息增益
if temp>ans:
divideV = T[i] # 始终存贮产生最大信息增益的分割点
ans = temp # 存贮最大的信息增益
return ans,divideV
# 进行决策,选择合适的属性进行划分
def decision_tree(self,X,Y,b):
gain_1,devide_1 = self.gainFloat(0,X,b) # 得到对应属性上的信息增益及划分点
gain_2,devide_2 = self.gainFloat(1,X,b)
if gain_1 >= gain_2: # 选择信息增益大的属性作为划分属性
self.seg_future.append(self.future[0])
self.seg_value.append(devide_1)
V = devide_1
p = 0
else:
self.seg_future.append(self.future[1])
self.seg_value.append(devide_2)
V = devide_2
p = 1
left_total = 0
right_total = 0
for i in range(self.m): # 计算划分之后每一部分的分类结果,在采样后的样本上计算
if X[i,p] <= V:
left_total = left_total + Y[i] # 分类得分
else:
right_total = right_total + Y[i]
if left_total > right_total:
flagg = 0
else:
flagg = 1
self.flag.append(flagg) # flag表示着分类的情况
# 得到样本在当前基学习器上的预测,在原始样本上预测
def pridect(self):
hlist = np.ones((self.m,))
if self.seg_future[-1]=='密度': p = 0
else: p = 1
if self.flag[-1]==0: # 此时小于等于V的样本预测为1
for i in range(self.m):
if self.x[i,p] <= self.seg_value[-1]:
hlist[i] = 1
else: hlist[i] = -1
else: # 此时大于V的样本预测是1
for i in range(self.m):
if self.x[i,p] <= self.seg_value[-1]:
hlist[i] = -1
else:
hlist[i] = 1
return hlist
def mysign(self,H): # 改进的sign函数
h = H
for i in range(len(H)):
if H[i] < 0: h[i] = -1
elif H[i]>0: h[i] = 1
else: h[i] = int(1-2*np.round(np.random.rand()))
return h
# 训练过程,进行集成
def train(self):
H = np.zeros(self.m)
self.H_predict = [] # 存贮每一个集成之后的分类结果
for t in range(self.T):
X,Y,b = self.boostStrap()
self.decision_tree(X,Y,b) # 得到基学习器分类结果
hlist = self.pridect() # 计算该基学习器的预测值
H = np.add(H,hlist) # 得到 t 个分类器集成后的分类结果(加权集成)
self.H_predict.append(self.mysign(H))
# 打印相关结果
def myPrint(self):
tplt_1 = "{0:<10}\t{1:<10}\t{2:<10}\t{3:<10}"
print(tplt_1.format('轮数','划分属性','划分点','何时取1?'))
for i in range(self.T):
if self.flag[i]==0:
print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
'x <= V'))
else:
print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
'x > V'))
print()
print('------'*10)
print()
print('%-6s'%('集成个数'),end='')
self.print_2('样本',[i+1 for i in range(17)])
print()
print('%-6s'%('真实标签'),end='')
self.print_1(self.y)
print()
for num in range(self.T):
print('%-10s'%(str(num+1)),end='')
self.print_1(self.H_predict[num])
print()
def print_1(self,h):
for i in h:
print('%-10s'%(str(np.int(i))),end='')
def print_2(self,str1,h):
for i in h:
print('%-8s'%(str1+str(i)),end='')
# 绘图
def myPlot(self):
Rx = []
Ry = []
Bx = []
By = []
for i in range(self.m):
if self.y[i]==1:
Rx.append(self.x[i,0])
Ry.append(self.x[i,1])
else:
Bx.append(self.x[i,0])
By.append(self.x[i,1])
plt.figure(1)
l1, = plt.plot(Rx,Ry,'r+')
l2, = plt.plot(Bx,By,'b_')
plt.xlabel('密度')
plt.ylabel('含糖率')
plt.legend(handles=[l1,l2],labels=['好瓜','坏瓜'],loc='best')
for i in range(len(self.seg_value)):
if self.seg_future[i]=='密度':
plt.plot([self.seg_value[i],self.seg_value[i]],[0.01,0.5])
else:
plt.plot([0.2,0.8],[self.seg_value[i],self.seg_value[i]])
plt.show()
def main():
bag = Bagging(11)
bag.train()
bag.myPrint()
bag.myPlot()
if __name__== '__main__':
main()
最终得到的结果如下:
轮数 划分属性 划分点 何时取1?
0 密度 0.3515 x > V
1 密度 0.244 x > V
2 含糖率 0.291 x > V
3 含糖率 0.0705 x <= V
4 密度 0.245 x > V
5 含糖率 0.373 x > V
6 密度 0.697 x > V
7 含糖率 0.415 x > V
8 密度 0.245 x > V
9 含糖率 0.08 x > V
10 含糖率 0.057 x > V
------------------------------------------------------------
集成个数 样本1 样本2 样本3 样本4 样本5 样本6 样本7 样本8 样本9 样本10 样本11 样本12 样本13 样本14 样本15 样本16 样本17
真实标签 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
1 1 1 1 1 1 1 1 1 1 -1 -1 -1 1 1 1 1 1
2 1 1 1 1 1 1 1 1 1 -1 -1 -1 1 1 1 1 1
3 1 1 1 1 -1 -1 1 -1 -1 -1 -1 -1 1 1 1 -1 1
4 1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 1 1 -1 -1 1
5 1 -1 1 -1 1 -1 1 -1 -1 -1 -1 -1 1 1 -1 -1 1
6 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1
7 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 1
8 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 1
9 1 -1 -1 -1 1 1 1 1 1 -1 -1 -1 1 1 -1 -1 1
10 1 1 1 1 1 1 1 1 1 -1 -1 1 1 1 -1 -1 1
11 1 1 1 1 1 1 1 1 1 -1 -1 1 1 1 -1 -1 1
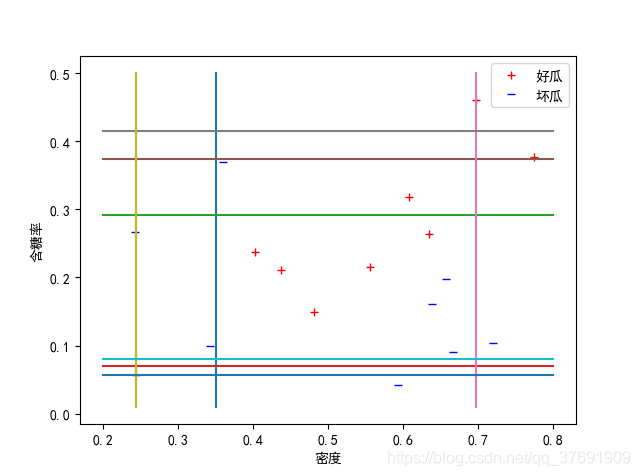
可以发现,结果集成的分类器在原始数据集上表现的并不好, 有很多样本被错分。
在仔细分析之后,个人感觉如果只单纯地使用一部分样本去计算信息增益等,可能并不好。 因为这是一个连续属性,首先要进行划分点的确定,如果只使用其中一部分样本进行选择,则可能划分点就过于随机,完全不适合原始数据集的划分。比如原始数据是[1,2,3,4,5],随机抽样后得到的数据集是[1,2,1,1,3],则在该数据集上的划分点就过于集中在值比较小的部分,当在原始数据集上进行分类时,就会产生较大偏差。
因此,为了保证划分点的分布均匀性,同时体现出自助采样的效果,最后选择使用带有权重的样本进行训练。 首先,通过自助采样得到一个新的样本集,但是此时不是直接用该样本集进行学习,而是通过该样本集来确定原始数据集中每一个样本的权重(此时多次出现的样本权重较大,没有出现的样本权重为0)。 之后,类似于AdaBoost,使用带权重的所有原数据集进行基学习器的构建,不同之处仅在于AdaBoost是根据上一轮的训练误差来更新样本权值,是串行的;而此处Bagging中每一轮之间没有任何关联,是并行的,它是根据自助采样得到的结果进行样本权重更新。
具体代码如下:
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
class Bagging:
# 导入数据
def loadData(self):
dataset = pd.read_excel('./WaterMelon_3.0.xlsx',encoding = 'gbk') # 读取数据
Attributes = dataset.columns # 所有属性的名称
m,n = np.shape(dataset) # 得到数据集大小
dataset = np.matrix(dataset)
for i in range(m): # 将标签替换成 好瓜 1 和 坏瓜 -1
if dataset[i,n-1]=='是': dataset[i,n-1] = 1
else : dataset[i,n-1] = -1
self.future = Attributes[1:n-1] # 特征名称(属性名称)
self.x = dataset[:,1:n-1] # 样本
self.y = dataset[:,n-1].flat # 实际标签
self.m = m # 样本个数
def __init__(self,T):
self.loadData()
self.T = T # 迭代次数
self.seg_future = list() # 存贮每一个基学习器用来划分的属性
self.seg_value = list() # 存贮每一个基学习器的分割点
self.flag = list() # 标志每一个基学习器的判断方向。
# 取0时 <= value 的样本标签为1,取1时 >value 的样本标签为1
self.w = 1.0/self.m * np.ones((self.m,)) # 初始的权重
def booststrap(self): # 自助采样
b = []
for i in range(self.m):
b.append(int(np.floor(np.random.uniform(0,17))))
for i in range(self.m):
count = b.count(i)
self.w[i] = count/self.m
# 计算交叉熵
def entropyD(self,D): # D 表示样本的编号,从0到16
pos = 0.0000000001
neg = 0.0000000001
for i in D:
if self.y[i]==1: pos = pos + self.w[i] # 标签为1的权重
else: neg = neg + self.w[i] # 标签为-1的权重
P_pos = pos/(pos+neg) # 标签为1占的比例
P_neg = neg/(pos+neg) # 标签为-1占的比例
ans = - P_pos * math.log2(P_pos) - P_neg * math.log2(P_neg) # 交叉熵
return ans
# 获得在连续属性上的最大信息增益及对应的划分点
def gainFloat(self,p): # p为对应属性编号(0表示密度,1表示含糖率)
a = []
for i in range(self.m): # 得到所有属性值
a.append(self.x[i,p])
a.sort() # 排序
T = []
for i in range(len(a)-1): # 计算每一个划分点
T.append(round((a[i]+a[i+1])/2,4))
res = self.entropyD([i for i in range(self.m)]) # 整体交叉熵
ans = 0
divideV = T[0]
for i in range(len(T)): # 循环根据每一个分割点进行划分
left = []
right = []
for j in range(self.m): # 根据特定分割点将样本分成两部分
if(self.x[j,p] <= T[i]):
left.append(j)
else:
right.append(j)
temp = res-self.entropyD(left)-self.entropyD(right) # 计算特定分割点下的信息增益
if temp>ans:
divideV = T[i] # 始终存贮产生最大信息增益的分割点
ans = temp # 存贮最大的信息增益
return ans,divideV
# 进行决策,选择合适的属性进行划分
def decision_tree(self):
gain_1,devide_1 = self.gainFloat(0) # 得到对应属性上的信息增益及划分点
gain_2,devide_2 = self.gainFloat(1)
if gain_1 >= gain_2: # 选择信息增益大的属性作为划分属性
self.seg_future.append(self.future[0])
self.seg_value.append(devide_1)
V = devide_1
p = 0
else:
self.seg_future.append(self.future[1])
self.seg_value.append(devide_2)
V = devide_2
p = 1
left_total = 0
right_total = 0
for i in range(self.m): # 计算划分之后每一部分的分类结果
if self.x[i,p] <= V:
left_total = left_total + self.y[i]*self.w[i] # 加权分类得分
else:
right_total = right_total + self.y[i]*self.w[i]
if left_total > right_total:
flagg = 0
else:
flagg = 1
self.flag.append(flagg) # flag表示着分类的情况
# 得到样本在当前基学习器上的预测
def pridect(self):
hlist = np.ones((self.m,))
if self.seg_future[-1]=='密度': p = 0
else: p = 1
if self.flag[-1]==0: # 此时小于等于V的样本预测为1
for i in range(self.m):
if self.x[i,p] <= self.seg_value[-1]:
hlist[i] = 1
else: hlist[i] = -1
else: # 此时大于V的样本预测是1
for i in range(self.m):
if self.x[i,p] <= self.seg_value[-1]:
hlist[i] = -1
else:
hlist[i] = 1
return hlist
def mysign(self,H): # 改进sign函数
h = H
for i in range(len(H)):
if H[i] < 0: h[i] = -1
elif H[i]>0: h[i] = 1
else: h[i] = int(1-2*np.round(np.random.rand())) # 0的时候随机取值
return h
# 训练过程,进行集成
def train(self):
H = np.zeros(self.m)
self.H_predict = [] # 存贮每一个集成之后的分类结果
for t in range(self.T):
self.booststrap() # 自助采样
self.decision_tree() # 得到基学习器分类结果
hlist = self.pridect() # 计算该基学习器的预测值
H = np.add(H,hlist) # 得到 t 个分类器集成后的分类结果(加权集成)
self.H_predict.append(self.mysign(H))
# 打印相关结果
def myPrint(self):
tplt_1 = "{0:<10}\t{1:<10}\t{2:<10}\t{3:<10}"
print(tplt_1.format('轮数','划分属性','划分点','何时取1?'))
for i in range(self.T):
if self.flag[i]==0:
print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
'x <= V'))
else:
print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
'x > V'))
print()
print('------'*10)
print()
print('%-6s'%('集成个数'),end='')
self.print_2('样本',[i+1 for i in range(17)])
print()
print('%-6s'%('真实标签'),end='')
self.print_1(self.y)
print()
for num in range(self.T):
print('%-10s'%(str(num+1)),end='')
self.print_1(self.H_predict[num])
print()
def print_1(self,h):
for i in h:
print('%-10s'%(str(np.int(i))),end='')
def print_2(self,str1,h):
for i in h:
print('%-8s'%(str1+str(i)),end='')
# 绘图
def myPlot(self):
Rx = []
Ry = []
Bx = []
By = []
for i in range(self.m):
if self.y[i]==1:
Rx.append(self.x[i,0])
Ry.append(self.x[i,1])
else:
Bx.append(self.x[i,0])
By.append(self.x[i,1])
plt.figure(1)
l1, = plt.plot(Rx,Ry,'r+')
l2, = plt.plot(Bx,By,'b_')
plt.xlabel('密度')
plt.ylabel('含糖率')
plt.legend(handles=[l1,l2],labels=['好瓜','坏瓜'],loc='best')
for i in range(len(self.seg_value)):
if self.seg_future[i]=='密度':
plt.plot([self.seg_value[i],self.seg_value[i]],[0.01,0.5])
else:
plt.plot([0.2,0.8],[self.seg_value[i],self.seg_value[i]])
plt.show()
def main():
bag = Bagging(11)
bag.train()
bag.myPrint()
bag.myPlot()
if __name__== '__main__':
main()
最终结果如下:
轮数 划分属性 划分点 何时取1?
0 含糖率 0.2925 x > V
1 含糖率 0.2045 x > V
2 密度 0.6815 x > V
3 含糖率 0.2925 x > V
4 含糖率 0.2045 x > V
5 密度 0.3815 x > V
6 密度 0.6815 x > V
7 密度 0.3515 x > V
8 含糖率 0.126 x > V
9 含糖率 0.2925 x > V
10 含糖率 0.2045 x > V
------------------------------------------------------------
集成个数 样本1 样本2 样本3 样本4 样本5 样本6 样本7 样本8 样本9 样本10 样本11 样本12 样本13 样本14 样本15 样本16 样本17
真实标签 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1
1 1 1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1
2 1 1 -1 1 1 1 -1 1 -1 1 -1 -1 -1 -1 1 -1 -1
3 1 1 -1 1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 1 -1 -1
4 1 1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1
5 1 1 1 1 1 -1 -1 1 -1 -1 -1 -1 -1 -1 1 -1 -1
6 1 1 1 1 1 1 -1 1 -1 -1 -1 -1 -1 -1 1 1 1
7 1 1 1 1 1 1 -1 1 -1 -1 -1 -1 -1 -1 1 1 1
8 1 1 1 1 1 1 -1 1 1 -1 -1 -1 -1 1 1 1 1
9 1 1 1 1 1 1 -1 1 -1 -1 -1 -1 1 1 1 -1 -1
10 1 1 1 1 -1 1 -1 1 -1 -1 -1 -1 1 -1 1 -1 -1
11 1 1 1 1 -1 1 -1 1 -1 -1 -1 -1 -1 -1 1 -1 -1
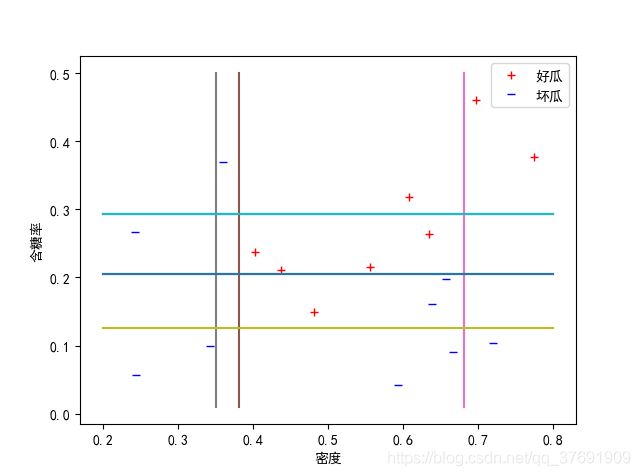
可以发现,此时的分类结果相对于之前的结果有一点改善,但是也不是特别精确,都没有AdaBoost方法得到的分类结果好。 这主要是因为AdaBoost主要侧重于降低偏差,所以会根据数据集无限拟合来使分类精度尽可能地高。 而Bagging则侧重于降低方差,所以该方法在特定的数据集上的分类精度往往不能达到很高很高,但是该方法对于数据的扰动不敏感,也就是说当数据产生了一些噪声扰动后,该方法也可以得到不错的分类效果。
当然,由于自助采样的存在,Bagging的结果随机性比较大,多次运行可能得到相差很大的分类结果。 而且,自助采样采用不同的随机数生成方式也会对结果造成影响。个人认为既然是随机取样,使用均匀分布恰当一些,但是也有人使用正态分布、泊松分布等不同方式。使用哪种方式更好或许和原始数据集的分布情况也有关系,在下能力有限,孰优孰劣也无法得知,还望各位不吝赐教!
8.6 为何Bagging很难提升朴素贝叶斯分类器的性能?
个人认为,朴素贝叶斯分类是通过使所有训练样本的后验概率达到最大而进行的,是在全样本集上进行的,从概率意义上说已经是在该特定训练集下的最优分类器。 而Bagging主要侧重于降低方差,但在使用全部训练集样本生成的朴素贝叶斯分类器中没有方差可以降低,不可能通过随机抽样的方法去提升其性能。
8.7 随机森林为何比决策树Bagging的训练速度更快?
因为随机森林除了在样本的选择上是随机抽取一部分外,在划分属性的选择上也是随机选择部分属性进行比较后得到最佳划分属性。但是Bagging是针对所有的属性进行最佳划分属性的选择,所以训练速度会慢。
8.8 MultiBoosting算法和 Iterative Bagging算法的优缺点。
MultiBoosting由于集合了Bagging,Wagging,AdaBoost,可以有效的降低误差和方差,特别是误差。但是训练成本和预测成本都会显著增加。
Iterative Bagging相比Bagging会降低误差,但是方差上升。由于Bagging本身就是一种降低方差的算法,所以Iterative Bagging相当于Bagging与单分类器的折中。
参考文章: https://blog.csdn.net/icefire_tyh/article/details/52194771
8.9 缺
8.10 提升k近邻分类器性能的集成学习算法。
可以使用Bagging来提升k近邻分类器的性能,每次随机抽样出一个子样本,并训练一个k近邻分类器,对测试样本进行分类。最终取最多的一种分类。
参考文章: https://blog.csdn.net/icefire_tyh/article/details/52194771