【Method】稀疏与压缩感知 | 图像稀疏性及压缩感知方法白话讲解

【Method】稀疏与压缩感知 | 图像稀疏性及压缩感知方法白话讲解

1. 为什么图像是可压缩的：图像空间的广阔

首先我们讨论一个重要的问题：为什么图像是可压缩的，亦或者说，图像是稀疏的。我们可以举一个例子：一个$20x20$的二值图像在空间中的可能性有$2^{400}$种，而人可以理解的图像也许只占$2^{400}$空间中的很小一部分，因此一幅图像只是这个巨大空间里的很小很小块分布。

2. 什么是Sparsity？

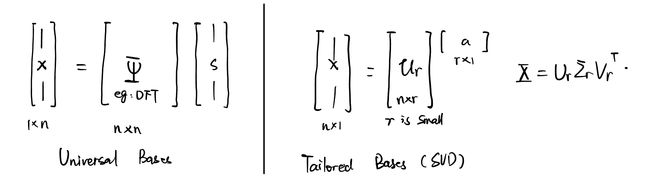
在自然数据中观察到的固有结构意味着数据在适当的坐标系中允许稀疏表示。大多数自然信号，如图像和音频，都是高度可压缩的。这种可压缩性意味着，当在适当的基础上写入信号时，只有少数模式处于活动状态，从而减少了为了准确表示而必须存储的值的数量。即可压缩信号$\mathbf{x}\in {\mathbb{R}}^{n\times n}$可以通过一个变换基$\Psi$和一个稀疏向量$\mathbf{s}\in {\mathbb{R}}^n$（即绝大多数元素为0元素的向量）相乘的形式表示：
$$\mathbf{x}=\Psi \mathbf{s}$$

注意区分：下图中左图为稀疏表示，其中$\mathbf{s}$为稀疏向量，右图为另一种表示数据压缩方式，即使用低维的a表示数据。

接着，我们想进一步实现一个大胆的想法，**如果只得到了$\mathbf{x}$的一部分元素（如10%），那么可以推断出$\mathbf{s}$中非零的傅里叶系数。**这便是压缩感知的目标。

但是，学过信号处理的同学都知道，对于一个信号（语音、图像等等），采样的频率要大于最大信号频率的两倍才可以很好的恢复信号，也就是鼎鼎大名的奈奎斯特采样定律。压缩感知突破了奈奎斯特采样定律，只通过高度欠采样的图像，实现较好的原始信号恢复。

3.压缩感知：简介

说了这么多，我们来看一个具体的例子把。假设图$\mathbf{x}$通过傅里叶变换$\Psi$到频域$\mathbf{s}$，对$\mathbf{s}$中信号进行阈值截断后，我们期望仍然可以重建出高质量的图像，这应该是不难的，因为我们知道，在傅里叶空间中，低频信号能量最高，也集中在中心区域，而去掉一些能量较低的高频信号对结果的影响实际上是不大的。

我们真正想解决的问题是下面这张图：如图所示，左上角的图是我们的采样结果，也就是低质量的观测值$\mathbf{y}$，是对真实图像$\mathbf{x}$的欠采样，我们希望通过$\mathbf{y}$变换得到$\mathbf{x}$的稀疏空间，从而重建出高质量的原始图像$\mathbf{x}$：

我们将上面过程数学化，也就是
$$\begin{gathered} \mathbf{y}=\mathbf{Cx} \\ =\mathbf{C}\Psi \mathbf{s} \end{gathered}$$
其中$\mathbf{C}$为欠采样矩阵。我们希望通过观测$\mathbf{y}$求解出稀疏向量$\mathbf{s}$，得到$\mathbf{s}$后我们就可已通过逆变换得到原始的$\mathbf{x}$。

4.压缩感知：数学公式

下图表示了$\mathbf{y}=\mathbf{Cx}=\mathbf{C}\Psi \mathbf{s}$的具体形式：

说明：$\Psi$是一种通用变换基，上图中可以认为是离散余弦基，也可以使用傅里叶基或者小波基。

根据上图我们不难发现：$\mathbf{y}$是一个0值较多的欠采样信号，因此该方程组是一个欠定方程组，$\mathbf{z}$有无数个解。因此我们需要用一些附加信息来找到这个非常特殊的$\mathbf{s}$，即最稀疏的 $\mathbf{s}$。

因此，我们的目标为：
$$\hat{s}=\arg \underset{x}{\min }\Vert \mathbf{C}\Psi \mathbf{s}-\mathbf{y}{\Vert }_2+\lambda L(\mathbf{s})$$

在上式中，$L(\mathbf{s})$为罚函数。可以有很多种设计方式用来约束$\mathbf{s}$，例如：

①$L(\mathbf{s})=\Vert \mathbf{s}\Vert$，一范数促进目标有更多0元素(一般来说为了的到更稀疏的$\mathbf{s}$，$L_1$范数使用较多)。

②当$L(\mathbf{s})=\Vert \mathbf{s}{\Vert }_2$，二范数更容易将误差分散在各个元素上，以便具有可能得最小半径。

下图为两种范数的结果，可以看到一范数的结果更加稀疏。

最直观的方法是0范数，但是0范数是非凸的，因此很难求解。在近年用高概率范数替换0范数，这将收敛到我们真正想要的稀疏方案

注意：前面的优化目标也可以写作：

特别的，当观测含有噪声时，优化目标如下

5.压缩感知实例

5.1 欠定系统的 $l_1$和稀疏解

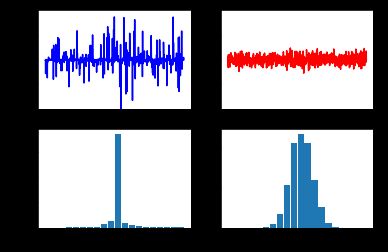
下面通过一个例子（python实现）观察两种范数作为罚函数的作用：

我们比较线性方程 y = Theta * s 的 L1 范数最小化解和 L2 范数最小化解，并绘制它们的曲线和直方图。

具体来说，代码中首先生成了一个随机的矩阵 Theta 和一个随机的向量 y，用于构造线性方程。然后，代码使用优化算法求解 L1 范数最小化问题，并得到最优解 s_L1，同时使用矩阵的伪逆计算了 L2 范数最小化问题的解 s_L2。

接下来，代码创建了一个包含四个子图的图形布局，分别绘制了 s_L1 和 s_L2 的曲线图以及它们的分布直方图。通过这些图形，可以比较 L1 范数最小化解和 L2 范数最小化解在数值上的差异以及它们的分布特征。

import numpy as np
import matplotlib.pyplot as plt
import os
from scipy.optimize import minimize
plt.rcParams['figure.figsize'] = [12, 18]
plt.rcParams.update({'font.size': 18})

# Solve y = Theta * s for "s"
n = 1000 # dimension of s
p = 200  # number of measurements, dim(y)
Theta = np.random.randn(p,n)
y = np.random.randn(p)

# L1 Minimum norm solution s_L1
def L1_norm(x):
    return np.linalg.norm(x,ord=1)

constr = ({'type': 'eq', 'fun': lambda x:  Theta @ x - y})
x0 = np.linalg.pinv(Theta) @ y # initialize with L2 solution
res = minimize(L1_norm, x0, method='SLSQP',constraints=constr)
s_L1 = res.x

# L2 Minimum norm solution s_L2
s_L2 = np.linalg.pinv(Theta) @ y 

fig,axs = plt.subplots(2,2)
axs = axs.reshape(-1)
axs[0].plot(s_L1,color='b',LineWidth=1.5)
axs[0].set_ylim(-0.2,0.2)
axs[1].plot(s_L2,color='r',LineWidth=1.5)
axs[1].set_ylim(-0.2,0.2)
axs[2].hist(s_L1,bins=np.arange(-0.105,0.105,0.01),rwidth=0.9)
axs[3].hist(s_L2,bins=np.arange(-0.105,0.105,0.01),rwidth=0.9)

plt.show()

左图为1范数得到的稀疏信号$\mathbf{s}$的时域和频域，右图为2范数时域和频域结果。不难发现，L1范数使得$\mathbf{s}$更稀疏。

5.2 从稀疏观测中恢复音频信号

对于稀疏信号$\mathbf{s}$而言，我们可以在不满足奈奎斯特采样定律的条件下对信号进行采样，也可以重建信号。

奈奎斯特采样定律：采样频率>2×信号最高频率，信号才不会丢失较多信息。采样频率过小，则容易发生Aliasing（混叠）。

下面我们以一个音频信号为例子：

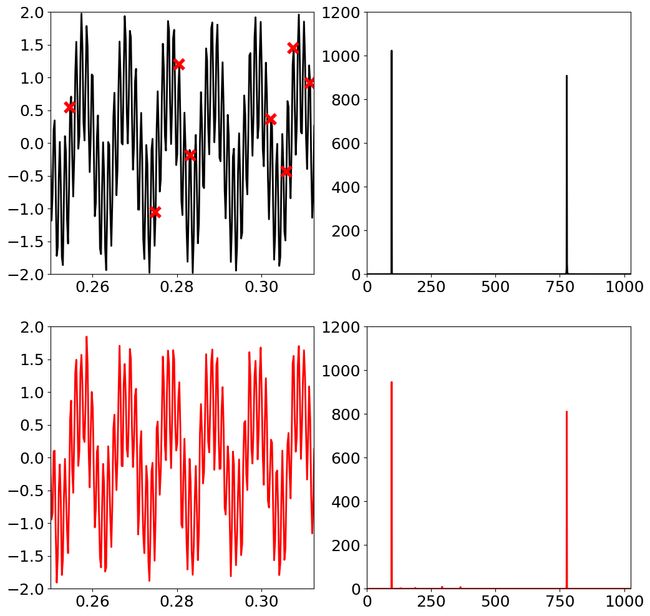
我们先对下面的模拟信号在1s内采样4096个点，采样的离散信号如左上角黑色的点所示，（只绘制了部分区域的图像）。

接着对离散信号进行随机采样，只采样128个点，如左上角红色点。接着我们可以使用matching pursuit方法（我也会在后续文章中进行讲解）计算出稀疏的s（右下角），从而进行逆变换为左下角的结果。

python代码如下：

import numpy as np
import matplotlib.pyplot as plt
import os
import sys
from scipy.fftpack import dct, idct
from scipy.optimize import minimize
sys.path.append(os.path.join('..','UTILS'))
from cosamp_fn import cosamp
# cosamp function is available at https://github.com/avirmaux/CoSaMP

plt.rcParams['figure.figsize'] = [12, 12]
plt.rcParams.update({'font.size': 18})


## Generate signal, DCT of signal

n = 4096 # points in high resolution signal
t = np.linspace(0,1,n)
x = np.cos(2 * 97 * np.pi * t) + np.cos(2 * 777 * np.pi * t)
xt = np.fft.fft(x) # Fourier transformed signal
PSD = xt * np.conj(xt) / n # Power spectral density 功率谱密度


## Randomly sample signal
p = 128 # num. random samples, p = n/32
perm = np.floor(np.random.rand(p) * n).astype(int)
y = x[perm]


## Solve compressed sensing problem
Psi = dct(np.identity(n)) # Build Psi
Theta = Psi[perm,:]       # Measure rows of Psi

s = cosamp(Theta,y,10,epsilon=1.e-10,max_iter=10) # CS via matching pursuit
xrecon = idct(s) # reconstruct full signal



## Plot
time_window = np.array([1024,1280])/4096
freq = np.arange(n)
L = int(np.floor(n/2))


fig,axs = plt.subplots(2,2)
axs = axs.reshape(-1)

axs[1].plot(freq[:L],PSD[:L],color='k',linewidth=2)
axs[1].set_xlim(0, 1024)
axs[1].set_ylim(0, 1200)

axs[0].plot(t,x,color='k',linewidth=2)
axs[0].plot(perm/n,y,color='r',marker='x',linewidth=0,ms=12,mew=4)
axs[0].set_xlim(time_window[0],time_window[1])
axs[0].set_ylim(-2, 2)

axs[2].plot(t,xrecon,color='r',linewidth=2)
axs[2].set_xlim(time_window[0],time_window[1])
axs[2].set_ylim(-2, 2)

xtrecon = np.fft.fft(xrecon,n) # computes the (fast) discrete fourier transform
PSDrecon = xtrecon * np.conj(xtrecon)/n # Power spectrum (how much power in each freq)

axs[3].plot(freq[:L],PSDrecon[:L],color='r',linewidth=2)
axs[3].set_xlim(0, 1024)
axs[3].set_ylim(0, 1200)

plt.show()

5.3 压缩感知的关键——信号采样的随机性

对于上图信号，如果我们均匀地以低于Nyquist采样定律进行采样，则很容易发生信号混叠。但是当我们使用随机的低于Nyquist采样定律较多的频率采样时候，可以通过完美重建出原始信号。

5.4 Sparsity and $L1$ Norm

为什么$L_1$ 范式可以约束求解结果的稀疏性呢？假设$\mathbf{s}=(s_1,s_2)$，直线上都为满足$y=\Theta \mathbf{s}$的点。我们的目标是找到norm最小的$\mathbf{s}$。

下图中两个坐标轴分别为$s_1,s_2$，我们需要找到的目标点使得norm最小，即同心的图形与直线相交时的最小距离。以$L_2$ norm为例，我们想像有一个从小放大的同心圆，那么同心圆和直线恰好相交时，交点坐标为$(s_1,s_2)$，不难看出交点向量是非稀疏的。并且我们有如下结论：

• $L_0$：能达到真正稀疏，但是是非凸优化问题，是NP hard；
• $L_1$：替代$L_0$，也能达到稀疏的结果；

6. 压缩感知：When it works？

前面我们简单介绍了压缩感知，那么有同学可能比较疑惑，为什么压缩感知有效，并且想要实现压缩感知，应该满足什么条件？

为什么压缩感知有效：

要想使得压缩感知可以成功实现，我们需要满足如下两点要求：

1. C 与$\Psi$不想关，即C的行 与$\Psi$的列正交；
2. 观测信号的稀疏度也要满足一定要求；

我们先来看看第一个要求：假设下图是几个比较好的欠采样矩阵$\mathbf{C}$：

下图是比较差的$\mathbf{C}$，也就是$\mathbf{C}$和$\Psi$相关性较大：

可以明显看出这样的$\mathbf{C}$是完全无法恢复稀疏的$\mathbf{s}$的。

第二个要求：观测信号的稀疏度$p$怎么选择？

稀疏度指的是向量中非0元素的个数，$\mathbf{y}$的稀疏度$p$和$\mathbf{s}$的稀疏度$k$一般满足如下关系($n$是$\mathbf{x}$的维度)：
$$p\propto O(klog(n/k))$$
注意：$O(\cdot )$取决于$C$相对于$\Psi$的不相干程度，越不想干则函数的放大比例越小，需要的观测越稀疏。

举个例子：我们可以根据$n$和$k$计算出我们的稀疏观测的稀疏度。假设$n=10^6$，$n=10^6$ ，$k=10^4(1\%)$，假设$O(l)=5\cdot l$，那么$p=5\cdot 10^{4}log(100)=10^5(10\%)$。即我们只需要观测图像只是原始图像的10%随机采样，即可重建出高质量的原图。

总结：稀疏变换后的结果越稀疏，我们需要的观测越稀疏。

参考资料

[1] https://www.youtube.com/watch?v=yDpz0PqULXQ&list=PLMrJAkhIeNNRHP5UA-gIimsXLQyHXxRty&index=18

[2] http://databookuw.com/databook.pdf