图像处理之梯度及边缘检测算子
文章目录
- 一、sobel 算子
- 二、Scharr算子
- 三、Roberts算子
- 四、拉普拉斯算子
梯度是一个量变化的速度,在数学中通常使用求导、求偏导获取梯度或者某一方向上的梯度。
在数字图像中梯度可以看为像素值分别在x,y方向上的变化速度,因为数字图像的离散型,以及像素是最小处理单元的特性,求数字图像的梯度时,不需要求导,只需要进行加减运算即可。(其实就是求导的差分近似形式).如下图所示:
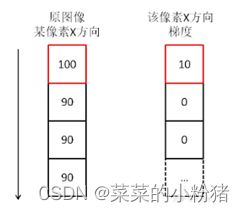
一、sobel 算子
Sobel算子包含两组 3 ∗ 3的矩阵,分别为横向及纵向模板,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。下面是 G x G_x Gx 和 G y G_y Gy的模板。
G x = [ + 1 0 − 1 + 2 0 − 2 + 1 0 − 1 ] ∗ A G_x= \left[ \begin{array} {cccc} +1&0&-1\\ +2 &0&-2\\ +1 &0&-1 \end{array} \right]*A Gx= +1+2+1000−1−2−1 ∗A
G y = [ + 1 + 2 + 1 0 0 0 − 1 − 2 − 1 ] ∗ A G_y= \left[ \begin{array} {cccc} +1&+2&+1\\ 0&0&0\\ -1&-2&-1 \end{array} \right]*A Gy= +10−1+20−2+10−1 ∗A
如上式, G x G_x Gx与 G y G_y Gy分别表示对图像A进行横向和纵向梯度检测得到的结果。
取二者平方和即可得到图像上每一点的梯度值,即在该点同时计算 x x x方向与 y y y方向的梯度。
G = G x 2 + G y 2 G=\sqrt{G_x^2+G_y^2} G=Gx2+Gy2
该点的梯度方向可以通过取这两个值的比的反正切 a r c t a n arctan arctan得到:
Θ = a r c t a n ( G y G x ) \Theta=arctan\left(\frac{G_y}{G_x}\right) Θ=arctan(GxGy)
实现代码如下:
def SobelX(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
result[i,j] =v
if(result[i,j]<threshold):
result[i,j]=0
return result
def SobelY(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] =h
if(result[i,j]<threshold):
result[i,j]=0
return result
def Sobel(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
G_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
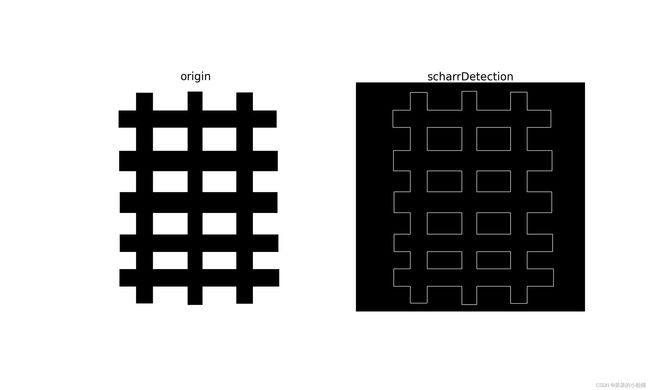
二、Scharr算子
Scharr算子是Sobel算子的一种特殊形式。其核的形式如下:
[ + 3 0 − 3 + 10 0 − 10 + 3 0 − 3 ] \left[ \begin{array} {cccc} +3&0&-3\\ +10 &0&-10\\ +3&0&-3 \end{array} \right] +3+10+3000−3−10−3
[ − 3 − 10 − 3 0 0 0 + 3 + 10 + 3 ] \left[ \begin{array} {cccc} -3&-10&-3\\ 0 &0&0\\ +3&+10&+3 \end{array} \right] −30+3−100+10−30+3
前面提到了,Sobel算子中核越大就能够更好的近似导数,准确度也更高。因此,在核比较小时如3×3时,Sobel核的准确度较差,使用Scharr算子代替3×3的Sobel核能够提高精度。因为加大了在x方向或y方向的权重,使得梯度角(梯度方向)不会距离x或y方向太远,因此误差也不会太大。例如,只求x方向的梯度时,核的中心点的x方向的两个权值远大于其它权值,这使得求得的梯度更靠近x方向,一定程度减小了误差。
def Scharr(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-3, 0, 3], [-10, 0, 10], [-3, 0, 3]])
G_y = np.array([[-3, -10, -3], [0, 0, 0], [3, 10, 3]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
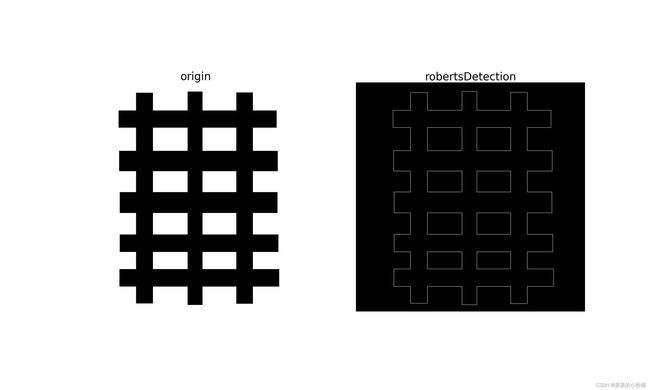
三、Roberts算子
[ − 1 0 0 1 ] \left[ \begin{array} {cccc} -1&0\\ 0&1\\ \end{array} \right] [−1001]
[ 0 − 1 1 0 ] \left[ \begin{array} {cccc} 0&-1\\ 1 &0\\ \end{array} \right] [01−10]
Roberts算子的核如上图所示,是一种简单的交叉差分算法,在求±45°的梯度时最有效。
相比于一般的水平竖直方向的差分算子,Roberts算子能够有效地保留边缘的角点,并且计算速度较快。缺点是对细节敏感导致对噪声也十分敏感。
实现代码:
def Roberts(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0], [0,1]])
G_y = np.array([[0, -1], [1,0]])
result = np.zeros(img.shape)
for i in range(0, width - 1):
for j in range(0, height - 1):
v = np.sum(G_x * img[i:i + 2, j:j + 2])
h = np.sum(G_y * img[i:i + 2, j:j + 2])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
四、拉普拉斯算子
拉普拉斯算子可由二阶导数定义:
Δ 2 ( x , y ) = ∂ 2 f ( x , y ) ∂ x 2 + ∂ 2 f ( x , y ) ∂ y 2 \Delta^2(x,y)=\frac{\partial^2f(x,y)}{\partial x^2}+\frac{\partial^2f(x,y)}{\partial y^2} Δ2(x,y)=∂x2∂2f(x,y)+∂y2∂2f(x,y)
而在数字图像中离散化,用二阶差分表示为:
∂ 2 f ( x , y ) ∂ x 2 ≈ Δ x f ( i + 1 , j ) − Δ x f ( i , j ) = [ f ( i + 1 , j ) − f ( i , j ) ] − [ f ( i , j ) − f ( i − 1 , j ) ] = f ( i + 1 , j ) + f ( i − 1 , j ) − 2 f ( i , j ) \begin{align*} \begin{split} \frac{\partial^2f(x,y)}{\partial x^2} &\approx \Delta_xf(i+1,j)-\Delta_xf(i,j) \\ &= \left[ f(i+1,j)-f(i,j) \right]- \left[f(i,j)-f(i-1,j) \right] \\ &=f(i+1,j)+f(i-1,j)-2f(i,j) \end{split} \end{align*} ∂x2∂2f(x,y)≈Δxf(i+1,j)−Δxf(i,j)=[f(i+1,j)−f(i,j)]−[f(i,j)−f(i−1,j)]=f(i+1,j)+f(i−1,j)−2f(i,j)
同理可得:
∂ 2 f ( x , y ) ∂ y 2 ≈ f ( i , j + 1 ) + f ( i , j − 1 ) − 2 f ( i , j ) \frac{\partial^2f(x,y)}{\partial y^2} \approx f(i,j+1)+f(i,j-1)-2f(i,j) ∂y2∂2f(x,y)≈f(i,j+1)+f(i,j−1)−2f(i,j)
所以拉普拉斯算子可以表示为:
Δ 2 ( x , y ) = f ( i + 1 , j ) + f ( i − 1 , j ) + f ( i , j + 1 ) + f ( i , j − 1 ) − 4 f ( i , j ) \Delta^2(x,y)=f(i+1,j)+f(i-1,j)+f(i,j+1)+f(i,j-1)-4f(i,j) Δ2(x,y)=f(i+1,j)+f(i−1,j)+f(i,j+1)+f(i,j−1)−4f(i,j)
其卷积核如下:
[ 0 1 0 1 − 4 1 0 1 0 ] \left[ \begin{array} {cccc} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{array} \right] 0101−41010
拉普拉斯算子法其实是一种图像边缘增强算子,常用于图像锐化,在增强边缘的同时也增强了噪声,因此使用前需要进行平滑或滤波处理。如下图,可以看出,在函数值发生突变的情况时,二阶导数能够增强突变点与其两侧的对比度。在数字图像中就是图像边缘处得到了增强,因此实现了图像的锐化。

代码实现如下:
def Laplacian(img):
temLaplacian = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])
height, width = img.shape[::-1]
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
result[i][j] = np.abs(np.sum(temLaplacian * img[i:i + 3, j:j + 3]))
return result
import numpy as np
import cv2
import imgShow as iS
def SobelX(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
result[i,j] =v
if(result[i,j]<threshold):
result[i,j]=0
return result
def SobelY(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] =h
if(result[i,j]<threshold):
result[i,j]=0
return result
def Sobel(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
G_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
def Sobel(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
G_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
def Scharr(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-3, 0, 3], [-10, 0, 10], [-3, 0, 3]])
G_y = np.array([[-3, -10, -3], [0, 0, 0], [3, 10, 3]])
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
v = np.sum(G_x * img[i:i + 3, j:j + 3])
h = np.sum(G_y * img[i:i + 3, j:j + 3])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
def Roberts(img,threshold):
height = img.shape[0]
width = img.shape[1]
G_x = np.array([[-1, 0], [0,1]])
G_y = np.array([[0, -1], [1,0]])
result = np.zeros(img.shape)
for i in range(0, width - 1):
for j in range(0, height - 1):
v = np.sum(G_x * img[i:i + 2, j:j + 2])
h = np.sum(G_y * img[i:i + 2, j:j + 2])
result[i,j] = np.sqrt((v ** 2) + (h ** 2))
if(result[i,j]<threshold):
result[i,j]=0
return result
def Laplacian(img):
temLaplacian = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])
height, width = img.shape[::-1]
result = np.zeros(img.shape)
for i in range(0, width - 2):
for j in range(0, height - 2):
result[i][j] = np.abs(np.sum(temLaplacian * img[i:i + 3, j:j + 3]))
return result
img=cv2.imread("./originImg/HorizontalAndVertical.jpg")
img=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
sobelImg=Sobel(img,56)
iS.showImagegray(sobelImg, img, 25, 15, 'sobelDetection', 'origin', './ProcessedImg/sobelDetection.jpg')
imageList=[]
origin_img=[img,'origin_img']
imageList.append(origin_img)
sobelx=SobelX(img,0)
sobel2=[sobelx,'Sobel_X']
imageList.append(sobel2)
sobely=SobelY(img,0)
sobel1=[sobely,'Sobel_Y']
imageList.append(sobel1)
sobelImg=Sobel(img,56)
sobel3=[sobelImg,'Sobel']
imageList.append(sobel3)
iS.showMultipleimages(imageList,25,25,'./ProcessedImg/sobelEdge.jpg')
img1=cv2.imread('./originImg/Goldhill.tif')
img1=cv2.cvtColor(img1,cv2.COLOR_BGR2GRAY)
LapImg=Laplacian(img1)
iS.showImagegray(LapImg, img1, 25, 15, 'LapImg', 'origin', './ProcessedImg/lapImg.jpg')
scharrImg=Scharr(img,56)
iS.showImagegray(scharrImg, img, 25, 15, 'scharrDetection', 'origin', './ProcessedImg/scharrDetection.jpg')
robertsImg=Roberts(img,56)
iS.showImagegray(robertsImg, img, 25, 15, 'robertsDetection', 'origin', './ProcessedImg/robertsDetection.jpg')
# cv2.imshow('sobely',sobely)
# cv2.waitKey(0)
# cv2.destroyAllWindows()
画图代码:
import matplotlib.pyplot as plt
import numpy as np
import math
#图像实际大小为 W*100 * H*100 像素 ,
def showImagegray(newImg,oldImg,W,H,newImgtitle,oldImgtitle,saveImgpath):
plt.figure(figsize=(W,H))
plt.subplot(121)
plt.title(oldImgtitle,fontsize=30)
plt.axis('off')
plt.imshow(oldImg, cmap='gray')
plt.subplot(122)
plt.title(newImgtitle,fontsize=30)
plt.axis('off')
plt.imshow(newImg, cmap='gray')
# plt.tight_layout() # 调整整体空白
plt.savefig(saveImgpath)
plt.show()
def showMultipleimages(imageList,W,H,saveImgpath):
imageLength=len(imageList)
plt.rcParams['figure.figsize'] = (W,H)
col=row=math.ceil(np.sqrt(imageLength))
fig, a = plt.subplots(col, row)
m = 0
for i in range(col):
for j in range(row):
a[i][j].set_title(imageList[m][1])
a[i][j].imshow(imageList[m][0], cmap=plt.cm.gray)
m += 1
#去掉边框和刻度
for ax in a.flat:
ax.set_axis_off()
fig.tight_layout() # 调整整体空白
plt.subplots_adjust(wspace=0.2, hspace=0.2) # 调整子图间距
plt.savefig(saveImgpath)
plt.show()