机器学习15：神经网络-Neural Networks
神经网络是特征交叉的更复杂版本。本质上，神经网络会学习适当的特征组合。本文主要介绍神经网络的结构、隐藏层、激活函数等内容。
目录
1.神经网络：结构
3.激活函数
3.1 常用激活函数
3.2 小结
4.神经网络小练习
4.1 第一个神经网络
4.2 神经网络螺旋
5.参考文献
1.神经网络：结构
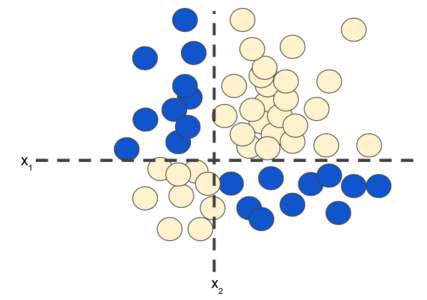
在【机器学习8】中，笔者介绍了特征组合（特征交叉），用于解决非线性的分类问题，如图 1 所示：
图 1. 非线性分类问题
“非线性” 意味着我们无法使用以下形式（如：
）的模型准确预测标签， 换句话说，“决策面”不是一条线。之前，我们将 特征交叉 视为非线性问题建模的一种可能方法。现在考虑以下数据集：
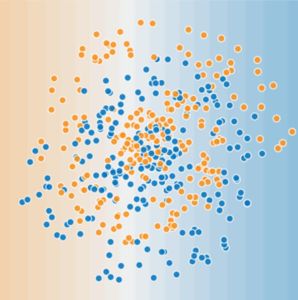
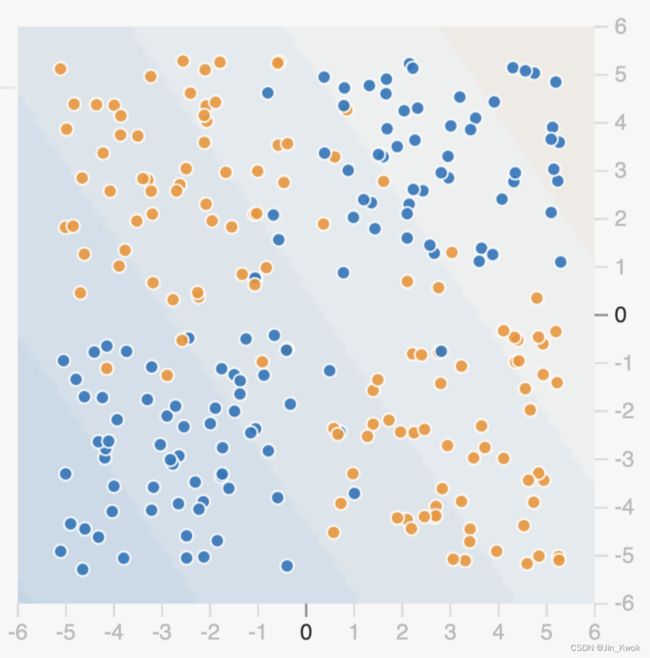
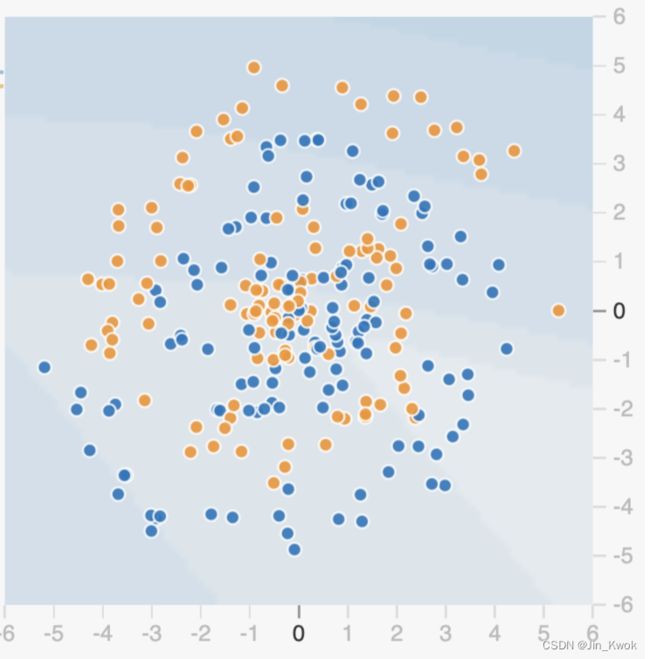
图 2. 更困难的非线性分类问题
很显然，图 2 所示的数据集无法使用线性模型求解。为了了解神经网络如何帮助解决非线性问题，我们首先将线性模型表示为图形：
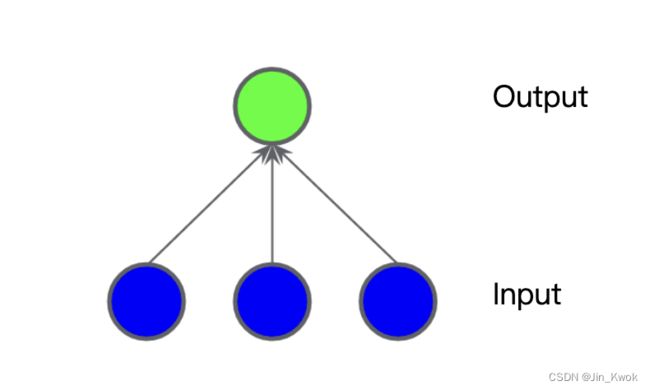
图 3. 线性模型如图所示
图 3 中，每个蓝色圆圈代表一个输入特征，绿色圆圈代表输入的加权和。我们如何改变这个模型以提高其处理非线性问题的能力？
2.隐藏层
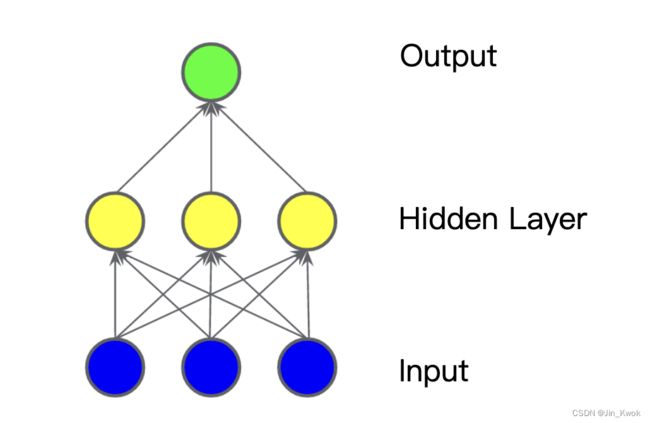
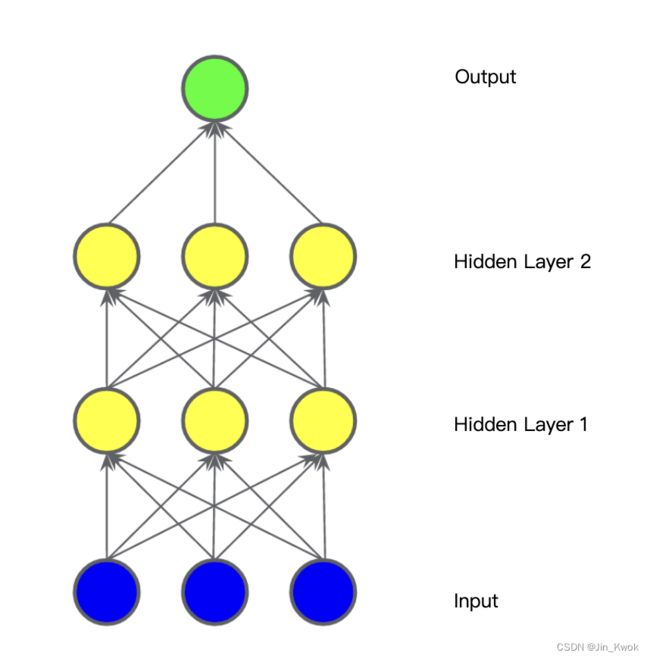
在图 4 所示的模型中，我们添加了中间值的 “隐藏层”。隐藏层中的每个黄色节点都是蓝色输入节点值的加权和。输出是黄色节点的加权和。
图 4. 两层模型图
这个模型是线性的吗？是的——它的输出仍然是其输入的线性组合。在下图所示的模型中，我们添加了第二个加权和隐藏层。
图 5. 三层模型图
这个模型仍然是线性的吗？——是的。当我们将输出表示为输入的函数并进行简化时，我们将得到输入的另一个加权和。该总和无法有效地模拟图 2 中的非线性问题。
3.激活函数
为了对非线性问题进行建模，我们可以直接引入非线性。我们可以通过非线性函数对每个隐藏层节点进行管道传输。
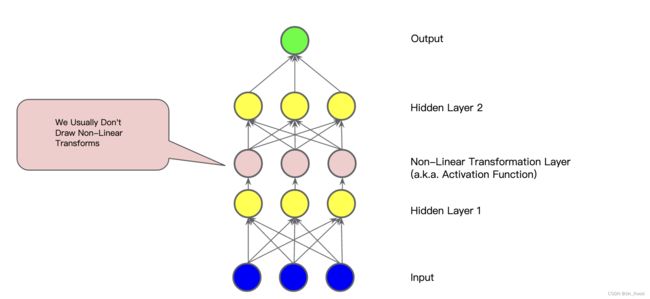
在图 6 所示的模型中，隐藏层 1 中每个节点的值在传递到下一层的加权和之前先通过非线性函数进行变换。这种非线性函数称为激活函数。
图 6. 具有激活函数的三层模型图
现在我们已经添加了激活函数，添加层会产生更大的影响。通过在非线性上叠加非线性，我们可以对输入和预测输出之间非常复杂的关系进行建模。简而言之，每一层都在原始输入上有效地学习更复杂、更高级别的函数。
3.1 常用激活函数
以下 sigmoid 激活函数将加权和转换为 0 到 1 之间的值。
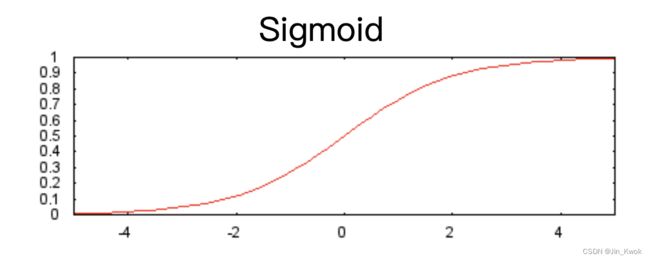
sigmoid 函数的图像如图 7 所示：
图 7.Sigmoid 激活函数
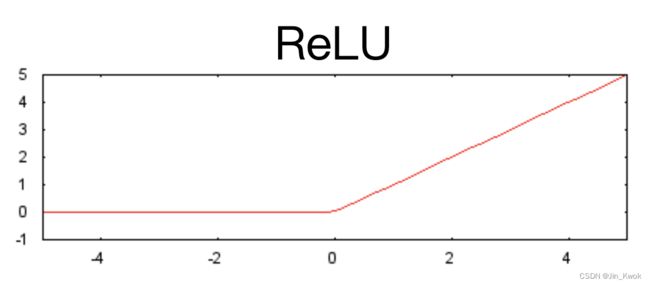
下面的修正线性单元激活函数（简称 ReLU）通常比 sigmoid 等平滑函数效果更好，同时也更容易计算。
由于 ReLU 具有更有用的响应范围，在实践中，ReLU 具有一定优越性。相较于 sigmoid ，ReLU 两侧下降得相对较快。
图 8.ReLU 激活函数
事实上，任何数学函数都可以充当激活函数。假设 
代表我们的激活函数（Relu、Sigmoid 或其他函数）。因此，网络中节点的值由以下公式给出：
TensorFlow 为许多激活函数提供开箱即用的支持。我们可以在 TensorFlow 的神经网络包装器列表中找到这些激活函数。不过，在学习机器学习时，建议从 ReLU 开始。
3.2 小结
根据上面的介绍，关于“神经网络” 模型，通常具有如下标准组件：
- 一组节点，类似于神经元，分层组织。
- 一组权重，表示每个神经网络层与其下面的层之间的连接。下面的层可能是另一个神经网络层，或某种其他类型的层。
- 一组偏差，每个节点一个。
- 转换层中每个节点的输出的激活函数。不同的层可能有不同的激活函数。
需要注意的是：神经网络不一定总是比特征交叉更好，但神经网络确实提供了一种在许多情况下效果良好的灵活替代方案。
4.神经网络小练习
4.1 第一个神经网络
对于如图 9 所示的非线性数据集，我们将训一个小神经网络。神经网络将为我们提供一种学习非线性模型的方法，而无需使用显式特征交叉。
图 9.非线性数据集
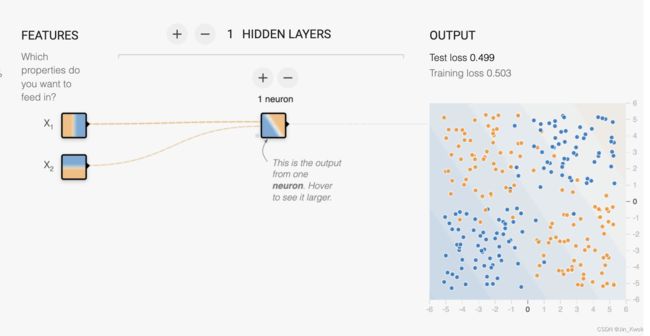
任务 1：给定的模型将我们的两个输入特征组合到一个神经元中。这个模型会学习任何非线性吗？运行它来确认您的猜测。
图 10.隐藏层一个节点+线性激活函数
显然，由于激活设置为 Linear，因此该模型无法学习任何非线性。损失非常高，我们说模型与 数据拟合不足。
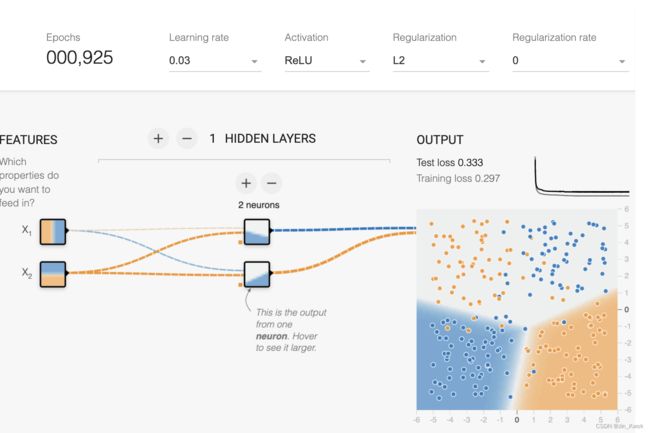
任务 2：尝试将隐藏层中的神经元数量从 1 个增加到 2 个，并尝试从线性激活更改为 ReLU 等非线性激活。如此，能创建一个可以学习非线性的模型吗？它可以有效地对数据进行建模吗？
结果：如图 11 所示，非线性激活函数可以学习非线性模型。然而，具有 2 个神经元的单个隐藏层无法反映该数据集中的所有非线性，并且即使没有噪声也会产生很高的损失：它仍然 不适合数据。这些练习是不确定的，因此有些运行无法学习有效的模型，而其他运行则可以做得很好。最好的模型可能没有您期望的形状！
图 11.隐藏层两个节点+ReLU激活函数
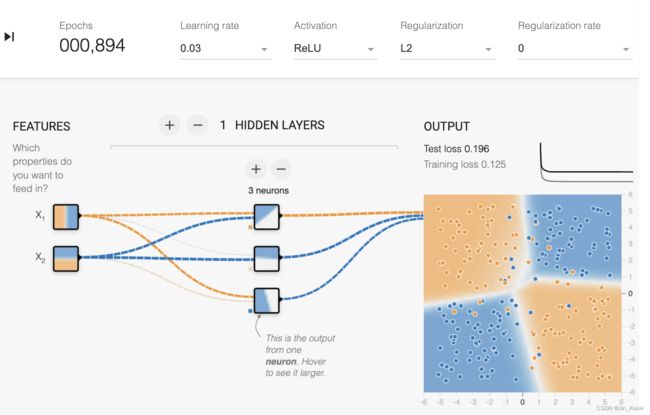
任务 3：尝试使用 ReLU 等非线性激活将隐藏层中的神经元数量从 2 个增加到 3 个。它可以有效地对数据进行建模吗？每次运行的模型质量有何不同？
结果：如图 12 所示，具有 3 个神经元的单个隐藏层足以对数据集进行建模（无噪声），但并非所有运行都会收敛到良好的模型。3 个神经元就足够了，因为 XOR 函数可以表示为 3 个半平面的组合（ReLU 激活）。在具有 3 个神经元和 ReLU 激活的良好模型中，将有 1 个具有几乎垂直线的图像，检测 X1 为正（或负；符号可以切换），1 个具有几乎水平线的图像，检测 X1 的符号 X2 和 1 个带有对角线的图像，检测它们的相互作用。
图 12.隐藏层三个节点+ReLU激活函数
任务 4：通过添加或删除隐藏层和每层神经元继续进行实验。还可以随意更改学习率、正则化和其他学习设置。 可以使用的最小神经元数和层数是多少，才能使测试损失达到 0.177 或更低？
结果：具有 3 个神经元的单个隐藏层可以对数据进行建模，但没有冗余，因此有时候无法学习到好的模型。具有超过 3 个神经元的单层具有更多冗余，因此更有可能收敛到良好的模型。
正如我们所看到的，只有 2 个神经元的单个隐藏层无法很好地对数据进行建模。如果尝试一下，将会发现输出层中的所有项目只能是由这两个节点的线条组成的形状。在这种情况下，更深的网络可以比单独的第一个隐藏层更好地对数据集进行建模：第二层中的各个神经元可以通过组合第一层中的神经元来建模更复杂的形状，例如右上象限。虽然添加第二个隐藏层仍然可以比单独第一个隐藏层更好地对数据集进行建模，但向第一层添加更多节点以使更多线条成为第二层构建其形状的套件的一部分可能更有意义。
图 12 二个隐藏层三个节点+ReLU激活函数
然而，第一个隐藏层只有 1 个神经元的模型无论多深都无法学习到好的模型。这是因为第一层的输出仅沿一个维度（通常是对角线）变化，这不足以很好地对该数据集进行建模。无论多么复杂，后面的层都无法弥补这一点；输入数据中的信息已不可恢复地丢失。
对于像这样的简单问题，如果我们不尝试建立一个小型网络，而是拥有许多包含大量神经元的层，该怎么办？正如我们所看到的，第一层将能够尝试许多不同的线斜率。第二层将有能力将它们累积成许多不同的形状，并在后续层中形成大量的形状。
通过允许模型通过如此多不同的隐藏神经元考虑如此多不同的形状，我们已经为模型创建了足够的空间，可以轻松地过度拟合训练集中的噪声，从而允许这些复杂的形状匹配训练数据的缺点而不是普遍的基本事实。在此示例中，较大的模型可能具有复杂的边界以匹配精确的数据点。在极端情况下，大型模型可以学习单个噪声点周围的 “岛屿”，这称为 记忆 数据。通过允许模型变得更大，我们会发现它实际上通常比仅具有足够神经元来解决问题的更简单模型表现更差。
4.2 神经网络螺旋
如图 13 所示，该数据集是一个嘈杂的螺旋。显然，线性模型在这里会失败，但即使是手动定义的特征交叉也可能很难构建。
图 13. “嘈杂”的数据集
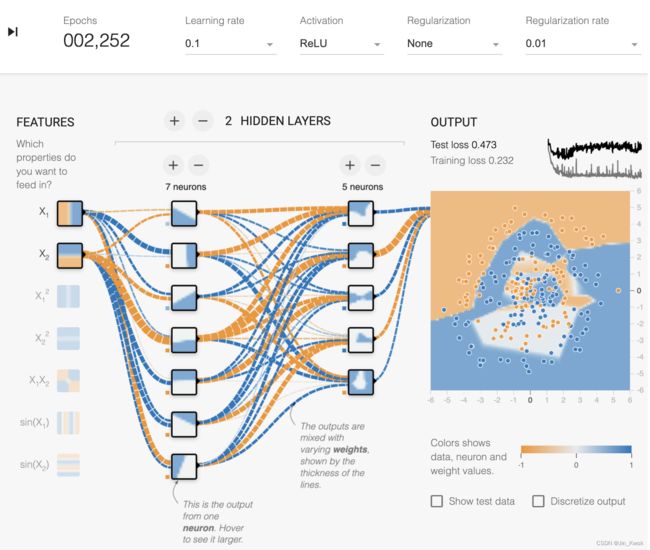
任务 1：仅使用 X1和 X2 训练尽可能最好的模型。随意添加或删除层和神经元，更改学习设置，例如学习率、正则化率和批量大小。您可以获得的最佳测试损失是多少？模型输出表面的光滑程度如何？
任务 2：即使使用神经网络，通常也需要进行一定量的特征工程才能实现最佳性能。尝试添加额外的叉积特征或其他转换，例如 sin(X 1 ) 和 sin(X 2 )。你有更好的模型吗？模型输出表面是否更加平滑？
图 14. “嘈杂”的数据集训练结果
上面的任务1和任务2，通过实验发现，对于这种“嘈杂”的数据集，训练模型时需要更多的层、神经元、组合特征才能训练出较低损失的模型。
5.参考文献
链接-https://developers.google.cn/machine-learning/crash-course/introduction-to-neural-networks/video-lecture