通过KMP算法掌握有限状态机
一、KMP 算法概述
KMP指的是Knuth-Morris-Pratt 字符串查找算法,提到字符串拼配,程序员们会很容易的想到遍历搜素,即在一组给定的字符串中查找特定的字串pattern。暴力遍历思路如下:
int search(String pat, String txt) {
int M = pat.length;
int N = txt.length;
for (int i = 0; i <= N - M; i++) {
int j;
for (j = 0; j < M; j++) {
if (pat[j] != txt[i+j])
break;
}
// pat 全都匹配了
if (j == M) return i;
}
// txt 中不存在 pat 子串
return -1;
}
暴力求解的思路很简单,就是将长字符串的所有字符作为开头字符与制定pattern比对,只要有一个字符不一致,则向后寻找新的开头字符,直到长字符串的结尾。可以看到该算法的时间复杂度为两层循环的乘积,即O(MN)。
而KMP算法它会花费空间来记录一些信息,这些所谓的信息其实是构造了一个有限状态机的状态迁移条件集合,而具体如何迁移则类似于动态规划的思想。所以说KMP有两个知识点:1、有限状态机 2、动态规划
借助状态迁移的好处是字符串不会回退,即不需要对元素进行重复比较,这样可以裁剪大量的重复计算,例如如下情况时穷举与KMP的差异:
穷举:

KMP:

当然,KMP为何如此智能,可以跳过重复计算。这就需要先搞清楚有限状态机的原理与作用
二、有限状态机
有限状态机是一种用来进行对象行为建模的工具,其作用主要是描述对象在它的生命周期内所经历的状态序列,以及如何响应来自外界的各种事件。通俗来讲,有限状态机就是一种通过表格来组织的switch-case结构,由于抽象除了各种概念,使得状态机的逻辑严谨性与扩展性要好于switch-case语句。
状态机可归纳为4个要素,即现态、条件、动作、次态。“现态”和“条件”是因,“动作”和“次态”是果。详解如下:
①现态:是指当前所处的状态。
②条件:又称为“事件”。当一个条件被满足,将会触发一个动作,或者执行一次状态的迁移。
③动作:条件满足后执行的动作。动作执行完毕后,可以迁移到新的状态,也可以仍旧保持原状态。动作不是必需的,当条件满足后,也可以不执行任何动作,直接迁移到新状态。
④次态:条件满足后要迁往的新状态。“次态”是相对于“现态”而言的,“次态”一旦被激活,就转变成新的“现态”了
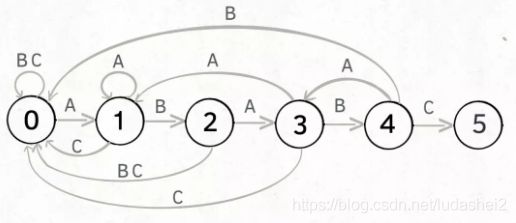
KMP可以按照状态机的定义来组织,例如pat=“ABABC”的字符串匹配:

可以将已匹配到的字符数量作为状态,匹配的字符作为触发条件,而进行状态改变可作为对应的动作
匹配过程会出现多种状态,例如匹配到A时,此时的现态为0(未匹配到一个字符),满足状态转移条件,那么就可以做动作,即将状态由0改为1,其中1就是次态。
通过上图来看,将字符串匹配过程抽象为状态机的状态迁移过程十分合理。但是这并不是KMP算法的核心。例如下图这种情况:

当匹配已经到达ABAB时,此时相当于状态机的状态变为4,接下来遇到C、A、B三个字符时的状态迁移分别为:
- 当遇到字符C时,状态自然切换为5,匹配完成,且成功
- 当遇到字符A时,按照暴力穷举的做法,一定是将待查找字符串向下移动一个所以,继续从新对pat进行匹配,但是图中切换到了状态3,即保留已匹配三个字符的结果。
- 当遇到字符A时,与暴力穷举的做法一致,将现态切换到了状态0,即恢复为最初状态。
可以看到状态机概念只是提供了一种设计框架为KMP算法来用,但是状态机的迁移(即条件如何触发动作,以及各状态间的关系)才是KMP的核心。为什么KMP可以知道何时回退状态到原始状态而何时回退到中间状态呢?这其中便是动态规划的思想,动态规划通俗来说就是使用前面的计算结果来计算接下来的结果。这是动态规划dp表的生产过程,那么倒着来用就是状态回退的依据。
根据动态规划的规则,可以设计如下的dp表来存放状态迁移的信息。
dp[j][c] = next
0 <= j < M,代表当前的状态
0 <= c < 256,代表遇到的字符(ASCII 码)
0 <= next <= M,代表下一个状态
//例如
dp[4]['A'] = 3 表示:
当前是状态 4,如果遇到字符 A,
pat 应该转移到状态 3
dp[1]['B'] = 2 表示:
当前是状态 1,如果遇到字符 B,
pat 应该转移到状态 2
假设现在已经知道dp表的全部内容,那么使用该表来做字符串匹配的步骤如下:
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
// 如果达到终止态,返回匹配开头的索引
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
可以看到,有限状态机在有了状态转移表(也就是动态规划概念中的dp表)后,可以很简单的完成字符串匹配。但到这里还没涉及到KMP的核心:如何来得到dp表(状态转移表)
三、动态规划思想的KMP算法
KMP聪明之处在于回退状态时比较机智,它不会发现不匹配后,将状态迁移为初始状态,这一特定其实是由一个影子变量做到的,所谓影子状态,就是和当前状态具有相同的前缀。比如下面这种情况:

当前状态j = 4,其影子状态为X = 2,它们都有相同的前缀 “AB”。因为状态X和状态j存在相同的前缀,所以当状态j准备进行状态重启的时候(遇到的字符c和pat[j]不匹配),可以通过X的状态转移图来获得最近的重启位置。比如说刚才的情况,如果状态j遇到一个字符 “A”,应该转移到哪里呢?首先状态 4 只有遇到 “C” 才能推进状态,遇到 “A” 显然只能进行状态重启。状态j会把这个字符委托给状态X处理,也就是dp[j][‘A’ ] = dp[X][‘A’]:

以上过程很微妙,仔细观察X的作用,你也许会问,这个X怎么知道遇到字符 “B” 要回退到状态 0 呢?因为X永远跟在j的身后,状态X如何转移,在之前就已经算出来了。它其实类似于动态规划的”上一个结果“概念,即当前状态需要回退时需要基于上一结果的信息来进行,当然此处的”上一结果“并非上一状态,而是基于”最大相同前缀“来划分。
有了以上认知,就可以将kmp理解为动态规划的计算过程,以下为KMP构建状态迁移表的代码实现:
public class KMP {
private int[][] dp;
private String pat;
public KMP(String pat) {
this.pat = pat;
int M = pat.length();
// dp[状态][字符] = 下个状态
dp = new int[M][256];
// base case
dp[0][pat.charAt(0)] = 1;
// 影子状态 X 初始为 0
int X = 0;
// 当前状态 j 从 1 开始
for (int j = 1; j < M; j++) {
for (int c = 0; c < 256; c++) {
if (pat.charAt(j) == c)
dp[j][c] = j + 1;
else
dp[j][c] = dp[X][c];
}
// 更新影子状态,注意与search函数相关语句的对比
X = dp[X][pat.charAt(j)];
}
}
}
先解释一下这一行代码:
// base case
dp[0][pat.charAt(0)] = 1;
这行代码是 base case,只有遇到 pat[0] 这个字符才能使状态从 0 转移到 1,遇到其它字符的话还是停留在状态 0(Java 默认初始化数组全为 0)。
影子状态X是先初始化为 0,然后随着j的前进而不断更新的。下面看看到底应该如何更新影子状态X:
int X = 0;
for (int j = 1; j < M; j++) {
...
// 更新影子状态
// 当前是状态 X,遇到字符 pat[j],
// pat 应该转移到哪个状态?
X = dp[X][pat.charAt(j)];
}
更新X其实和search函数中更新状态j的过程是非常相似的:
int j = 0;
for (int i = 0; i < N; i++) {
// 当前是状态 j,遇到字符 txt[i],
// pat 应该转移到哪个状态?
j = dp[j][txt.charAt(i)];
...
}
其中的原理非常微妙,注意代码中 for 循环的变量初始值,可以这样理解:后者是在txt中匹配pat,前者是在pat中匹配pat[1:],状态X总是落后状态j一个状态,与j具有最长的相同前缀。所以我把X比喻为影子状态,似乎也有一点贴切。
另外,构建 dp 数组是根据 base case dp[0][…]向后推演。这就是我认为 KMP 算法就是一种动态规划算法的原因,下图为针对pat="ABABC"构建的dp表(已删除全部为0的部分):
[0][65]:1 [0][66]:2 [0][67]:0 [0][68]:0
[1][65]:1 [1][66]:2 [1][67]:0 [1][68]:0
[2][65]:3 [2][66]:0 [2][67]:0 [2][68]:0
[3][65]:1 [3][66]:4 [3][67]:0 [3][68]:0
[4][65]:3 [4][66]:0 [4][67]:5 [4][68]:0