leetcode：491. 递增子序列

题目来源

• leetcode：increasing-subsequences

题目描述

题目解析

回溯

即枚举出所有的子序列，然后判断当前的子序列是否是严格递增的，然后还需要去重。所以我们需要解决两个问题：

• 如何枚举出所有的子序列
• 如何判断子序列是严格递增的
• 如何对子序列去重

怎么枚举出所有的子序列呢？

• 可以遍历nums中数组的每一个值，每个元素都有两种选择，要么加入tmp数组，要么不加。

 void dfs(std::vector<int> &nums, std::vector<int> &tmp, int idx){
        // 超出了
        if(idx >= nums.size()){
            for (int i = 0; i < tmp.size(); ++i) {
                printf("%d\t", tmp[i]);
            }
            printf("\n");
            return;
        }

        // 加入
        tmp.push_back(nums[idx]);
        dfs(nums, tmp, idx + 1);

        // 不加入
        tmp.pop_back();
        dfs(nums, tmp, idx + 1);
    }

怎么确保是递增的序列呢？

• 在遍历时，只有当前nums中的元素大于等于temp的最后元素时，该元素才有可能被放入到temp中

void dfs(std::vector<int> &nums, std::vector<int> &tmp, int idx){
        // 超出了
        if(idx >= nums.size()){
            for (int i = 0; i < tmp.size(); ++i) {
                printf("%d\t", tmp[i]);
            }
            printf("\n");
            return;
        }

        if(tmp.empty()||nums[idx]>=tmp.back()){
            tmp.push_back(nums[idx]);
            dfs(nums, tmp, idx + 1);
            tmp.pop_back();
        }
        
        dfs(nums, tmp, idx + 1);
    }

又因为题目要求递增子序列只有至少有两个元素，所以

• 遍历完nums数组之后，如果tmp数组的大小>=2，那么tmp数组就是返回的一部分。

 void dfs(std::vector<int> &nums, std::vector<int> &tmp, int idx){
        // 超出了
        if(idx >= nums.size()){
            if(tmp.size() >= 2){
                for (int i = 0; i < tmp.size(); ++i) {
                    printf("%d\t", tmp[i]);
                }
                printf("\n");
            }

            return;
        }

        if(tmp.empty()||nums[idx]>=tmp.back()){
            tmp.push_back(nums[idx]);
            dfs(nums, tmp, idx + 1);
            tmp.pop_back();
        }

        dfs(nums, tmp, idx + 1);
    }

此时递归树如下。

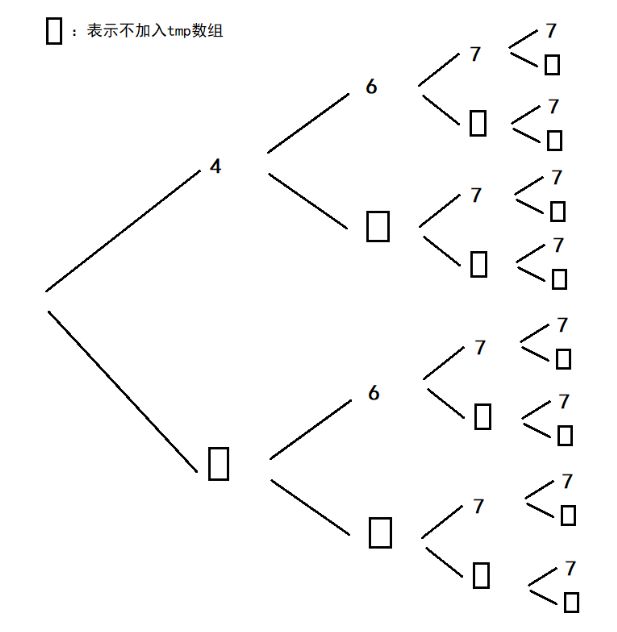
但是这样子会出现一个问题，有重复的tmp。如下图，相同颜色线的就是重复值

所以得去重。观察发现有重复得树枝都是在相邻的元素是相同的这种情况，于是我们可以这么做：如果 tmp 不为空，且当前元素和 tmp 中的最后一个元素相等，我们不考虑不将当前元素加入 tmp 中这一分支。从而解题思路如下：

• 遍历数组中每一个元素，并判断是否将其放入temp中
• 只有当前nums中的元素大于等于temp的最后元素时，该元素才有可能被放入到temp中
  • 当nums中当前元素等于temp的最后元素时，必须将其放入
  • 当nums中当前元素大于temp的最后元素时，则分别考虑放与不放的两种情况

class Solution {
    std::vector<std::vector<int>> ans;

    void dfs(std::vector<int> &nums, std::vector<int> &tmp, int idx){
        // 超出了
        if(idx >= nums.size()){
            if(tmp.size() >= 2){
                ans.push_back(tmp);
            }

            return;
        }

        if(tmp.empty()||nums[idx]>=tmp.back()){
            tmp.push_back(nums[idx]);
            dfs(nums, tmp, idx + 1);
            tmp.pop_back();
        }


        if(idx>0 && !tmp.empty() && nums[idx]==tmp.back()) return;//去重
        
        dfs(nums, tmp, idx + 1);
    }

public:
    vector<vector<int>> findSubsequences(vector<int>& nums){
        std::vector<int> tmp;
        dfs(nums, tmp, 0);
        return ans;
    }
};

思路二

上面的思路是当前碰到的一个元素，做判断，然后选择是否加入递归trace。下面我们是将所有所有的值做判断和递归。不考虑去重的递归树如下：

//上图对应的代码
for(int i = beg;i<nums.size();++i){
    if(asolution.empty()||nums[i]>=asolution.back()){
        asolution.push_back(nums[i]);
        subUpsequences(nums, i+1,asolution);
        asolution.pop_back();
    }       
}

这样，首先，加入结果集的位置就不是递归完成后的叶子节点了。因为叶子节点一定是7，这样像[4, 6]这样的结果就无法放入结果集了。所以放入结果集的位置是函数以开始，判断如下(目的是将树上所有符合结果的节点，而不只是叶子节点的值加入结果集中。)：

//递归一开始，只要该结果长度大于2就放入结果集
if(asolution.size()>=2){
    res.push_back(asolution);
}

那么，我们应该如何去重呢？因为如图，有两个[4,6,7],两个[4,7],两个[6,7]都会被放入结果集

因此我希望，在某一轮选择中，重复的不要，直接跳过。

再考虑到如下前后都有1的测试集的存在，需要一个set来保存已经尝试过的选择。

class Solution {
    std::vector<std::vector<int>> ans;

    void dfs(std::vector<int> &nums, std::vector<int> &tmp, int startIndex){
        if(ans.size() >= 2){
            ans.push_back(tmp);
        }

        std::set<int> set;
        for (int i = startIndex; i < nums.size(); ++i) {
            if(set.count(nums[i])){
                continue;
            }
            set.insert(nums[i]);
            if(tmp.empty() || nums[i] >= tmp.back()){
                tmp.push_back(nums[i]);
                dfs(nums, tmp, i + 1);
                tmp.pop_back();
            }
        }
    }

public:
    vector<vector<int>> findSubsequences(vector<int>& nums){
        std::vector<int> tmp;
        dfs(nums, tmp, 0);
        return ans;
    }
};

动态规划

• dp思路