目标定位算法（三）之基于角度的定位算法

基于角度测量的定位算法

又叫纯方位目标定位，它的测量信息是目标与观测站之间的角度，包括方向角和俯仰角等。

1.双战角度定位

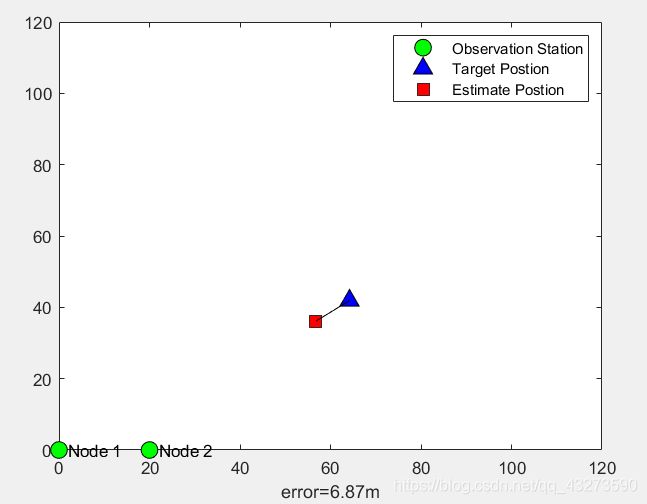
例：有两个观测站，其中A观测站的位置为坐标原点(0,0)， 另一个观测站位于x轴，位置为(d,0)。 两个观测站和目标同处于一个二维平面内，观测站对目标观测偏向角，并用该系统完成对目标的定位，MATLAB仿真如下：

function DoubleStationEstimate
%第一步:定位初始化
Length=100;              %场地空间,单位:米
Width=100;               %场地空间,单位:米
Node_number=2;           %两个观测站
Q=5e-4;                  %角度观测方差
%两个观测站之间的距离
dd=20;
Node(1).x=0;Node(1).y=0;
Node(2).x=dd;Node(2).y=0;
%目标的真实位置,这里随机给定
Target.x= Width * rand;
Target.y= Length * rand;
%第二步:各观测站对目标探测角度
Z=[];
for i=1:Node_number
    %获取观测角度
    Z(i)=atan2(Target.y-Node(i).y,Target.x-Node(i).x);
    %叠加上噪声,才是实际情况
    Z(i)=Z(i)+sqrt(Q)*randn;
end
%第三步:根据观测角度,用最小二乘法计算目标估计位置
H=[tan(Z(1)),-1;tan(Z(2)),-1];
b=[0,dd * tan(Z(2))]';
Estimate=inv(H'*H) *H'*b;        %目标的估计位置
Est_Target.x= Estimate(1);Est_Target.y= Estimate(2);

%画图
figure
hold on;box on;axis([0 120 0 120]); %输出图形的框架
for i= 1: Node_number
    h1= plot(Node(i).x, Node(i).y,'ko','MarkerFace','g','MarkerSize',10);
    text(Node(i).x+2,Node(i).y,[ 'Node ', num2str(i)]);
end
h2= plot(Target.x,Target.y,'k^','MarkerFace','b','MarkerSize', 10) ;
h3= plot(Est_Target.x,Est_Target.y,'ks','MarkerFace','r','MarkerSize',10);
line([Target.x,Est_Target.x],[Target.y,Est_Target.y] ,'Color' ,'k');
legend([h1,h2,h3 ],'Observation Station','Target Postion','Estimate Postion');
[Error_Dist]=DIST(Est_Target,Target);
xlabel(['error=',num2str( Error_Dist),'m']);

%子函数，计算两点间的距离
function[dist] = DIST(A,B)
dist= sqrt((A.x-B.x)^2+(A.y-B.y)-2);
end

2.三角测量法定位

三角测量法如下图所示，已知A、B、C三个观测站的坐标分别为$(x_a,y_a)、(x_b,y_b)、(x_c,y_c)$，目标位置相对观测站A、B、C的角度分别为∠AMC、∠BMC和∠CMA,求目标坐标M(x,y)。

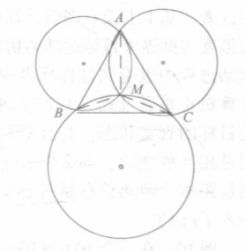
根据观测站A、B到目标点夹角∠AMB,则能够唯一确定一个圆，其圆心为$O_1,(x_1,y_1)$，半径为$r_1$，则存在公式:

求出目标点到3个圆心的距离，然后利用三角测量法求取目标M的坐标（x，y）。