目标定位算法(四)之移动目标定位算法
文章目录
- 移动目标定位算法
-
- 1.移动目标计算机仿真建模
- 2.基于距离观测的运动目标定位
- 3.纯方位角的运动目标定位
移动目标定位算法
实时探测目标并对目标进行实时定位。
1.移动目标计算机仿真建模
假定目标做匀速直线运动,第i个观测站的位置为(x,y),目标运动模型可以写成如下形式:

其中:
 注: Γ \Gamma Γ仿真时用G表示
注: Γ \Gamma Γ仿真时用G表示
u(k)的均方差Q=Wdiag([1,1]),w为一个可调节的参数,w<<1。v(k)的均方差R=5.
例:在一个100mx 100m的环境用计算机模拟一目标匀速运动的情形,如式(3-32),目标受到空气阻力影响,导致运动轨迹不一:定是匀速 直线的,即目标出现一定的轨迹抖动或弯曲。假定目标的初始位置为(0,0)、速度为(0.8,0.6), 过程噪声方差可以设置不同大小以观测计算机模拟的目标运动轨迹。
function TargetMotionModel %计算机模拟目标运动模型
dt=1; %采样时间,单位:秒
Time=30; %模拟总时长,也叫步数
X=zeros(4,Time); %目标在Time时间内各个时刻的状态初始化
x0=0;y0=0;vx=0.8;vy=0.6; %目标初始状态,包括位置和速度
X(:,1)=[x0,vx,y0,vy]'; %第一个时刻的状态,也叫初始状态
%系统信息,系统不同,状态转移矩阵和过程噪声驱动矩阵也不同
F=[1 dt 0 0;0 1 0 0;0 0 1 dt;0 0 0 1]; %公式(3-32)中的φ
G=[dt^2/2 0;dt 0;0 dt^2/2;0 dt]; %公式(3-32)中的r
Q=0.1; %公式(3-32)中u(k)的方差,过程噪声
u=sqrt(Q)*randn(2,Time) ;
%现在开始模拟目标随着时间推移,开始发生位置移动
for k= 2:Time
X(:,k)=F*X(:,k-1)+G*u(:,k);
end
figure
hold on;box on;%设置坐标轴的展示形式
plot(X(1,:),X(3,:),'-r.');%画出目标的运动轨迹
运行结果:
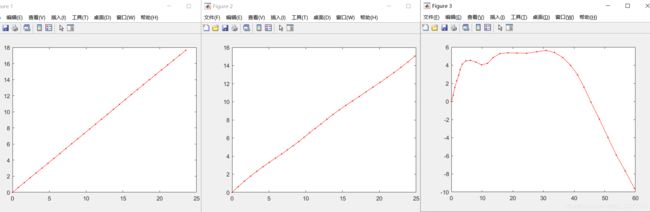
从左到右分别为,Q=0.00001时,目标基本匀速直线运动;Q=0.001时,目标的轨迹已经开始弯曲;Q=0.1时,已经无法相信目标是在做匀速直线运动哭了,因为这时的过程噪声非常大,导致目标的随机性也大。
2.基于距离观测的运动目标定位
假定有3个及以上的观测站对目标进行观测,第
i个观测站的测量方程为:
![]()
最后把这些观测站测量的距离信息传给融合中心,融合中心用最小二乘法就能实现对移动目标的动态定位。
例:在二维平面空间里,假定目标做匀速直线运动,目标运动的初始状态为x(0)=[0,1.5,20,1.4],目标受到摩擦力的影响存在过程噪声。在环境中有5个观测站对目标距离进行探测,观测站传感器的测量噪声方差为R=1,采样时间为Is,总运行时间为60s,MATLAB仿真如下:
function TrackingByDist %基于距离的跟踪(连续定位)
%系统模型的基本信息,包括场地大小、观测站位置.模型驱动参数等
Length=100; %场地空间,单位:米
Width=100; %场地空间,单位:米
Node_number=5; %观测站的个数,最少必须有3个
for i=1:Node_number %观测站的位置初始化,这里位置是随机给定的
Node(i).x= Width * rand;
Node(i).y= Length * rand;
Node(i).D= Node(i).x^2+Node(i).y^2; % 固定参数便于位置估计
end
T=1; %雷达采样时间,单位:秒
N= 60/T; %总的采样次数
delta_w=1e-3; %如果增大这个参数,目标真实轨迹就是曲线了
Q=delta_w*diag([0.5,1]) ; %过程噪声均值
R=1; %观测噪声方差
G=[T^2/2,0;T,0;0,T^2/2;0,T]; %过程噪声驱动矩阵
F=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1]; %状态转移矩阵
%开始模拟目标运动,观测在目标运动中同时采样,测量距离
X(:,1)=[0,1.5,20,1.4]; %目标初始位置、速度,状态参数格式[x,vx,y,vy]
Z=zeros( Node_number,N); %各观测站的传感器对位置的观测
Xn=zeros(2,N); %最小二乘估计出的位置
for t=2:N %状态方程的建模:目标运动,时间从1T→NT
X(:,t)=F*X(:,t-1)+G * sqrtm(Q) * randn(2,1); % 目标真实轨迹
end
for t=1:N %观测方程的建模:多观测站观测目标,时间从1T→NT
for i= 1:Node_number %名个观测站对1时刻目标距离测量
[d1,d2]=DIST(X(:,t),Node(i)); %dl是真实距离,d2是真实距离的平方
Z(i,t)= d1+sqrtm(R) * randn; %模拟观测的距离受到噪声的污染
end
%对当前时刻目标位置的二乘法估算
A=[];b=[];
for i=2:Node_number
A(i-1,:)= 2*[Node(i).x-Node( 1).x,Node(i).y-Node(1).y];
b(i-1,1)= [Z(1,t)^2-Z(i,t)^2+Node(i).D-Node(1).D];
end
Xn(:,t)= inv(A'*A)*A'*b; %得到目标当前时刻的位置
end
for t=1:N %计算位置偏差,即用最小二乘位置与计算机模拟的目标真实位置做差
error(t)=sqrt( (X(1,t)-Xn(1,t))^2+(X(3,t)-Xn(2,t))^2);
end
%画图
figure %轨迹图
hold on;box on;xlabel('x/m');ylabel('y/m'); %输出图形的框架
for i= 1: Node_number
h1= plot(Node(i).x, Node(i).y,'ko','MarkerFace','g','MarkerSize',10);
text(Node(i).x+2,Node(i).y,[ 'Node ', num2str(i)]);
end
h2=plot(X(1,:),X(3,:),'-r'); %目标的真实位置
h3=plot(Xn(1,:),Xn(2,:),'-k.'); %目标的估计位置
legend([h1,h2,h3 ],'Observation Station','Target Postion','Estimate Postion');
figure %偏差图
hold on;box on;xlabel( 'time/s' );ylabel( 'value of the deviation');
plot( error,'-ko' ,'MarkerFace','g');
%子函数,计算两点间的距离和距离平方
function [dist ,dist2]=DIST(A,B)
dist2=(A(1)-B.x)^2+(A(3)-B.y)^2; %距离的平方
dist=sqrt(dist2); %距离
end
运行结果:

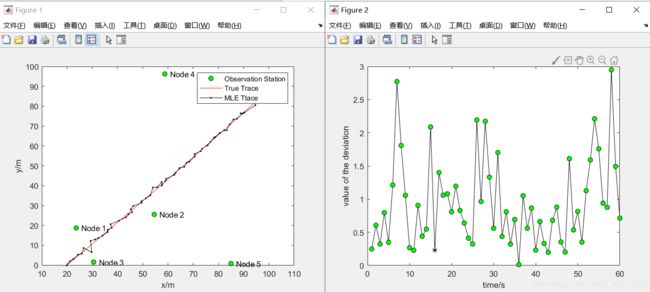
作图为定位估计与真实轨迹对比,右图为定位估计与真实位置偏差对比。
3.纯方位角的运动目标定位
观测站测量目标与自身的方位角的目标跟踪,又称为纯方位角的目标跟踪。当有多个观测站测量目标角度时,可以用最小二乘定位算法估计目标的位置。
第i个观测站的位置为 P ( x i , y i ) P(x_i,y_i) P(xi,yi),目标的位置为 T ( x , y ) T(x,y) T(x,y),则观测站测得的角度为 θ i \theta_i θi,
多个观测站测量,有如下关系: .

将上式转为矩阵的形式,如下:
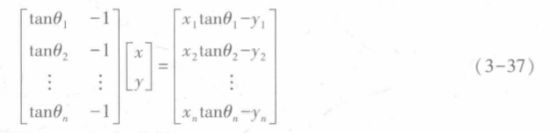
例:假定目标的运动模型为![]()
目标的初始状态为X(0)= [20,1.4,0,1.5],目标的过程噪声方差 Q = 1 ∗ 1 0 3 ∗ d i a g ( [ 0.5 , 1 ] ) Q= 1*10^3*diag([0.5,1]) Q=1∗103∗diag([0.5,1]),有5个观测站对目标进行探测,第i个观测站的测量方程为:

测量噪声 v i ( k ) v_i(k) vi(k)的方差R=0.1π/180,同样采样时间为T=1s,仿真时间为60s。MATLAB仿真如下:
function TrackingByAngle
% 定位初始化
Length=100; % 场地空间,单位:米
Width=100; % 场地空间,单位:米
Node_number=5; % 观测站的个数,也可以设置成3个,4个,但是最少必须要3个
for i=1:Node_number % 观测站的位置初始化,这里位置是随机给定的
Node(i).x=Width*rand;
Node(i).y=Length*rand;
end
T=1; %雷达扫描周期,
N=60/T; %总的采样次数,也称步长
delta_w=1e-4; % 如果增大这个参数,目标真实轨迹就是曲线了
Q=delta_w*diag([0.5,1]) ; % 过程噪声方差
R=0.1*pi/180; % 观测噪声方差
G=[T^2/2,0;T,0;0,T^2/2;0,T]; % 过程噪声驱动矩阵
F=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1]; % 状态转移矩阵
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
X=zeros(4,N); % 目标真实状态初始化
X(:,1)=[20,1.4,0,1.5]; % 目标初始位置、速度
Z=zeros(Node_number,N); % 各观测站的传感器对位置的观测
Xn=zeros(2,N); % 估计出的位置
for t=2:N % 目标运动
X(:,t)=F*X(:,t-1)+G*sqrtm(Q)*randn(2,1); %目标真实轨迹
end
for t=1:N
for i=1:Node_number
cita=hfun(X(:,t),Node(i)); % 观测角度
Z(i,t)=cita+sqrtm(R)*randn; % 模拟观测的角度受到噪声的污染
end
% 对当前时刻目标位置的二乘法的估算
A=[];b=[];
for i=1:Node_number
A(i,:)=[tan(Z(i,t)),-1];
b(i,1)=[Node(i).x*tan(Z(i,t))-Node(i).y];
end
inv(A'*A)*A'*b
Xn(:,t)=inv(A'*A)*A'*b; % 得到目标当前时刻的位置
end
for t=1:N % 偏差分析
error(t)=sqrt( (X(1,t)-Xn(1,t))^2+(X(3,t)-Xn(2,t))^2 );
end
%画图
figure
hold on;box on;xlabel('x/m');ylabel('y/m'); % 输出图形的框架
for i=1:Node_number
h1=plot(Node(i).x,Node(i).y,'ko','MarkerFace','g');
text(Node(i).x+2,Node(i).y,['Node ',num2str(i)]);
end
h2=plot(X(1,:),X(3,:),'-r');
h3=plot(Xn(1,:),Xn(2,:),'-k.');
legend([h1,h2,h3],'Observation Station','True Trace','MLE Ttace');
figure
hold on;box on;xlabel('time/s');ylabel('value of the deviation');
plot(error,'-ko','MarkerFace','g');
% 子函数
function angle=hfun(A,B) % 角度观测方程
angle=atan( (A(3)-B.y)/(A(1)-B.x) );

测量噪声从上到下分别为:R=0.001π/180、R=0.01π/180、R=0.1π/180。左边为轨迹,右边为定位偏差。
由结果可知,随着测量噪声增大,目标定位结果越来越差,即传感器信息足够可靠对提高精度至关重要,定位算法只是最大限度地减小误差。