(转载)BP神经网络的非线性系统建模(matlab实现)

1案例背景

        在工程应用中经常会遇到一些复杂的非线性系统,这些系统状态方程复杂,难以用数学方法准确建模。在这种情况下,可以建立BP神经网络表达这些非线性系统。方法把未知系统看成是一个黑箱,首先用系统输入输出数据训练BP神经网络,使网络能够表达该未知函数,然后用训练好的 BP神经网络预测系统输出。
        本章拟合的非线性函数为

        该函数的图像如图2-1所示：

图2-1 函数图像

2模型建立

        基于BP神经网络的非线性函数拟合算法流程可以分为BP神经网络构建,BP神经网络训练和 BP神经网络预测三步,如图2-2所示。

        BP神经网络构建根据拟合非线性函数特点确定BP神经网络结构,由于该非线性函数有两个输入参数，一个输出参数,所以BP神经网络结构为2--5—1,即输入层有2个节点,隐含层有5个节点,输出层有1个节点。
        BP神经网络训练用非线性函数输入输出数据训练神经网络,使训练后的网络能够预测非线性函数输出。从非线性函数中随机得到2000组输入输出数据,从中随机选择1900组作为训练数据,用于网络训练,100组作为测试数据,用于测试网络的拟合性能。
        神经网络预测用训练好的网络预测函数输出,并对预测结果进行分析。

3 MATLAB实现

        根据BP神经网络理论,用 MATLAB 软件编程实现基于BP神经网络的非线性拟合算法。

3.1 BP神经网络工具箱函数

        MATLAB软件中包含MATLAB神经网络工具箱。它是以人工神经网络理论为基础，用MATLAB 语言构造出了该理论所涉及的公式运算、矩阵操作和方程求解等大部分子程序以用于神经网络的设计和训练。用户只需根据自己的需要调用相关的子程序,即可以完成包括网络结构设计,权值初始化,网络训练及结果输出等在内的一系列工作,免除编写复杂庞大程序的困扰。目前,MATLAB神经网络工具箱包括的网络有感知器、线性网络、BP神经网络,径向基网络、自组织网络和回归网络等。BP神经网络主要用到newff,sim和 train 3个神经网络函数,各函数解释如下。

3.1.1. newff :BP神经网络参数设置函数函数功能:构建一个BP神经网络。

函数形式:

net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)P:输入数据矩阵。
T:输出数据矩阵。S:隐含层节点数。
TF:节点传递函数,包括硬限幅传递函数hardlim,对称硬限幅传递函数hardlims,线性传递函数 purelin、正切S型传递函数tansig,对数S型传递函数logsig.
BTF:训练函数，包括梯度下降BP算法训练函数traingd、动量反传的梯度下降BP算法训练函数traingdm,动态自适应学习率的梯度下降BP算法训练函数traingda,动量反传和动态自适应学习率的梯度下降BP算法训练函数 traingdx、Levenberg_Marquardt的 BP算法训练函数trainlm。
BLF:网络学习函数,包括BP学习规则learngd,带动量项的BP学习规则learngdm。

PF:性能分析函数,包括均值绝对误差性能分析函数mae,均方差性能分析函数mse。

IPF:输入处理函数。
OPF:输出处理函数。
DDF:验证数据划分函数。
一般在使用过程中设置前面6个参数,后面4个参数采用系统默认参数。

3.1.2.train: BP神经网络训练函数

函数功能:用训练数据训练BP神经网络。
函数形式:[net,tr] =train(NET,X,T,Pi,Ai)NET:待训练网络。
X:输入数据矩阵。

T:输出数据矩阵。
Pi:初始化输入层条件。

Ai:初始化输出层条件。

net:训练好的网络。

tr:训练过程记录。
一般在使用过程中设置前面3个参数,后面2个参数采用系统默认参数。

3.1.3. sim:BP神经网络预测函数

函数功能:用训练好的BP 神经网络预测函数输出。

函数形式:y=sim(net,x)
net:训练好的网络。
x:输入数据。
y:网络预测数据。

3.1.4完整matlab代码

        首先，根据非线性函数方程随机得到该函数的2000组输人输出数据,将数据存储在 data.mat文件中, input 是函数输入数据,output是函数输出数据。从输入输出数据中随机选取1900组数据作为网络训练数据,100组数据作为网络测试数据,并对训练数据进行归一化处理。

        其次，用训练数据训练BP 神经网络，使网络对非线性函数输出具有预测能力。

        最后，用训练好的BP神经网络预测非线性函数输出，并通过神经网络预测输出和期望输出

分析BP神经网络的拟合能力。

%% 该代码为基于BP神经网络的预测算法
%% 清空环境变量
clc
clear

%% 训练数据预测数据提取及归一化
%下载输入输出数据
load data input output

%从1到2000间随机排序
k=rand(1,2000);
[m,n]=sort(k);

%找出训练数据和预测数据
input_train=input(n(1:1900),:)';
output_train=output(n(1:1900));
input_test=input(n(1901:2000),:)';
output_test=output(n(1901:2000));

%选连样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);

%% BP网络训练
% %初始化网络结构
net=newff(inputn,outputn,5);

net.trainParam.epochs=100;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00004;

%网络训练
net=train(net,inputn,outputn);

%% BP网络预测
%预测数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
 
%网络预测输出
an=sim(net,inputn_test);
 
%网络输出反归一化
BPoutput=mapminmax('reverse',an,outputps);

%% 结果分析

figure(1)
plot(BPoutput,':og')
hold on
plot(output_test,'-*');
legend('预测输出','期望输出')
title('BP网络预测输出','fontsize',12)
ylabel('函数输出','fontsize',12)
xlabel('样本','fontsize',12)
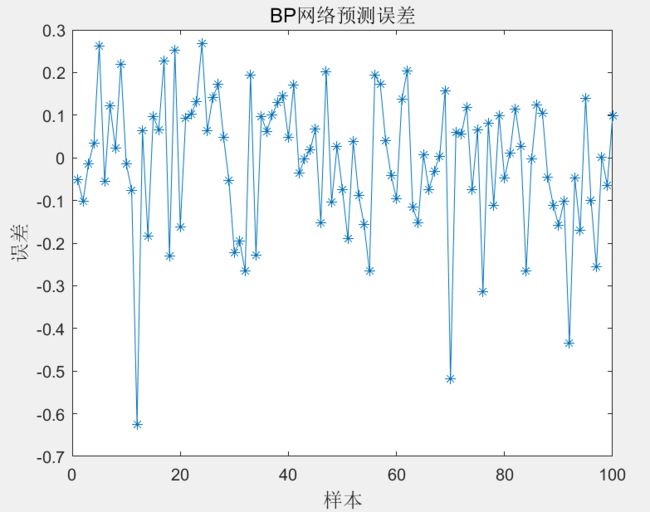
%预测误差
error=BPoutput-output_test;


figure(2)
plot(error,'-*')
title('BP网络预测误差','fontsize',12)
ylabel('误差','fontsize',12)
xlabel('样本','fontsize',12)

figure(3)
plot((output_test-BPoutput)./BPoutput,'-*');
title('神经网络预测误差百分比')

errorsum=sum(abs(error));

4结果分析

        用训练好的 BP 神经网络预测函数输出，预测结果、BP 神经网络预测输出和期望输出的误差如下图 所示。

        从上图可以看出,虽然BP神经网络具有较高的拟合能力,但是网络预测结果仍有一定误差,某些样本点的预测误差较大。后面案例中将讨论BP神经网络优化算法,以期得到更好的预测结果。

5案例扩展

5.1多隐含层 BP神经网络

        BP神经网络由输入层、隐含层和输出层组成,隐含层根据层数又可以分为单隐含层和多隐含层。多隐含层由多个单隐含层组成,同单隐含层相比,多隐含层泛化能力强、预测精度高，但是训练时间较长。隐含层层数的选择要从网络精度和训练时间上综合考虑,对于较简单的映射关系,在网络精度达到要求的情况下,可以选择单隐含层,以求加快速度;对于复杂的映射关系,则可以选择多隐含层,以期提高网络的预测精度。
        MATLAB神经网络工具箱中的newff函数可以方便地构建包含多个隐含层的BP神经网络,其调用函数如下:

net = newff(inputn,outputn,[5,5]);

        从运行时间和预测精度两个方面比较单隐含层BP神经网络和双隐含层BP神经网络的性能，网络结构相同，训练迭代都为100次，比较10次预测结果平均值，比较结果如表2-1 所列。

 

        从表2-1可以看出,双隐含层BP神经网络同单隐含层BP神经网络相比,预测精度有所提高,但是运行时间有所增加。

5.2 隐含层节点数

        BP神经网络构建时应注意隐含层节点数的选择,如果隐含层含节点数太少,BP神经网络不能建立复杂的映射关系,网络预测误差较大。但是如果节点数过多,网络学习时间增加,并且可能出现“过拟合”现象,就是训练样本预测准确,但是其他样本预测误差较大。不同隐含层节点数BP神经网络预测误差如表2-2所列。

        由于本案例拟合的非线性函数较为简单,所以BP神经网络预测误差随着节点数的增加而不断减少,但是对于复杂问题来说﹐网络预测误差随节点数增加一般呈现先减少后增加的趋势。

5.3训练数据对预测精度影响

        神经网络预测的准确性和训练数据的多少有较大的关系,尤其对于一个多输人多输出的网络,如果缺乏足够多的网络训练数据,网络预测值可能存在较大的误差。
        笔者曾经做过一个 BP神经网络预测实例,该实例通过建立一个4输入、5输出BP 神经网络预测实验结果。网络训练数据来自于真实实验﹐由于实验过程复杂,故只取到84组数据，选择其中80组数据作为BP神经网络训练数据,其余4组数据作为测试数据,训练后的BP神经网络预测结果如表2-3所列。
        从表2-3可以看出,由于缺乏训练数据,BP神经网络没有得到充分训练,BP神经网络预测值和期望值之间误差较大。
        笔者曾经做过一个类似的预测问题,该问题的目的是构建一个4输入4输出的 BP神经网络预测系统输出,训练数据来自于模型仿真结果。由于该模型可以通过软件模拟﹐所以得到多组数据,选择1500组数据训练网络,最后网络预测值同期望值比较接近。

5.4节点转移函数

MATLAB神经网络工具箱中newff函数提供了几种节点转移函数，主要包括以下三种。

        在网络结构和权值,阈值相同的情况下,BP神经网络预测误差和均方误差、输出层节点转移函数的关系如表2-4所列。

        从表2-4可以看出,隐含层和输出层函数的选择对BP神经网络预测精度有较大影响。一般隐含层节点转移函数选用logsig函数或tansig函数,输出层节点转移函数选用tansig或purelin函数。

5.5网络拟合的局限性

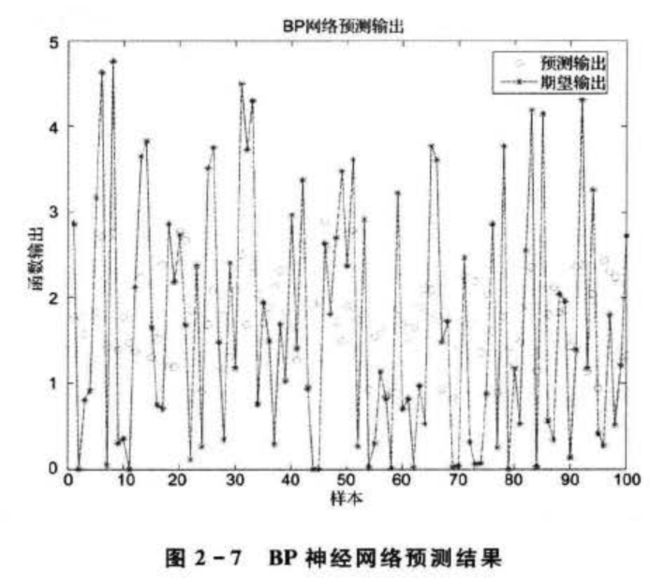
        BP神经网络虽然具有较好的拟合能力,但其拟合能力不是绝对的,对于一些复杂系统，BP神经网络预测结果会存在较大误差。比如对于

        其函数图形 如图 2-6 所示。

        随机选取该函数2000组输入输出数据,从中取1900组数据训练网络,100组数据测试网络拟合能力。采用单隐含层BP神经网络,网络结构为2—5—1,网络训练100次后预测函数输出,预测结果如图2-7所示。从图2-7可以看出,对于复杂的非线性系统,BP神经网络预测误差较大。该例说明BP神经网络的拟合能力具有局限性。