【高阶数据结构】并查集详解
并查集
- 并查集概述
- 并查集功能分析
- 数组实现并查集
- 并查集——森林实现
-
- 并查集——查找算法
- 并查集——合并算法
- 整体代码
并查集概述
并查集(Union Find),又称不相交集合(Disjiont Set),它应用于N个元素的集合求并与查询问题,在该应用场景中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。虽然该问题并不复杂,但面对极大的数据量时,普通的数据结构往往无法解决,并查集就是解决该种问题最为优秀的算法。
并查集功能分析
初始时:
元素:0 1 2 3 4 5 6 7
集合:0 1 2 3 4 5 6 7
元素:0 1 2 3 4 5 6 7
集合:0 1 2 3 4 0 6 7
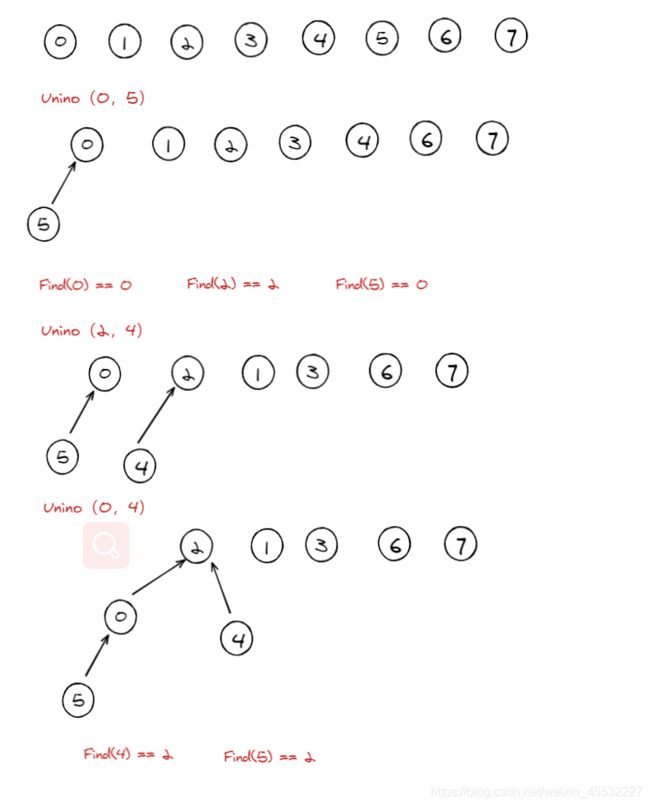
在这里将5,合并在0集合之中。(当然也可以将0,放在无在5集合之中)
也就是5将0认作老大,0就时该集合的老大。

Find(0) == 0
Find(5) == 0
Find(0) == Find(5) // 在同一个集合
Find(2) == 2
Find(5) == 0
Find(2) != Find(5) // 不在同一个集合
合并:Union(2,4)
元素:0 1 2 3 4 5 6 7
集合:0 1 2 3 2 0 6 7
将4 合并到2集合之中,同理2就是该集合的老大。

合并:Union(0,4)
首先4已经属于2集合,将2集合合并到0集合:
本来4的老大时2,现在要合并到0,所以在这里可以将2的老大也认0.
相当于4和2 都拜了新的老大0.
元素:0 1 2 3 4 5 6 7
集合:0 1 0 3 0 0 6 7
Find(2) == Find(5) // 在同一个集合
数组实现并查集
/**
* @ClassName Union_Find
* @Description :TODO
* @Author Josvin
* @Date 2021/01/14/21:00
*/
class UnionFind {
private int[] id;// 存储各个元素属于那个集合,他们的下标值表示他们的元素,值表示他们属于哪个集合
private int count;// 表示刚开始有多少集合(初始每个元素就是一个集合)
public UnionFind(int N) {
// 初始化
count = N;
id = new int[N];
for(int i = 0; i < N; i++) id[i] = i;
}
// 获取有多少集合
public int getCount() {
return count;
}
//判断 p 和 q 是不是一个集合
public boolean connected(int p, int q) {
return find(p) == find(q);
}
// 查找(找最后被合并到那个集合,也就是找集合老大)
public int find(int p) {
return id[p];
}
// 合并 (吧一个集合的合并到另一个集合,也就是换一个集合的老大)
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot) return;
for(int i = 0; i < id.length; i++)
if(id[i] == pRoot) id[i] = qRoot;
count--;// 当没合并一次,集合的数目就会少一个
}
}
在这里复杂度还是比较高的,主要还是合并过程复杂度O(n).
接下来就要介绍并查集的其他实现方法。
并查集——森林实现
使用森林存储集合之间的关系,属于同一集合的不同元素,都有一个相同的根节点,代表着这个集合。
当进行查找某元素属于哪个集合时,即遍历该元素到根节点,返回根节点所代表的集合;在遍历过程中使用路径压缩的优化算法,使整体树的形状更加扁平,从而优化查询的时间复杂度。
当进行合并时,即将两颗子树合为一颗树,将一颗子树的根节点指向另一颗子树的根节点;在合并时可按子树的大小,将规模较小的子树合并到规模较大的子树上,从而使树规模更加平衡,从而优化未来查询的时间复杂度。
并查集——查找算法
在查找时,普通的查找即通过id数组遍历至根节点,当p与当前集合id[p] 不同时(直到p与id[p] 相同时跳出循环),进行循环:p = id[p];
返回p的值。
public int find(int p) {
while(p != id[p]) p = id[p];
return p;
}
在查找时增加 路径压缩 的优化算法:
当p与当前集合id[p] 不同时(直到p与id[p] 相同时跳出循环),进行循环:
将p的父节点id[p] 更新为id[p] 的父亲节点id[id[p]];
p = id[p];
返回p的值。
public int find(int p) {
if(p != id[p]) id[p] = find(id[p]);
return id[p];
}
上边时一个递归写法;
循环写法:
public int find(int p) {
while(p != id[p]) {
id[p] = id[id[p]];
p = id[p];
}
return p;
}
并查集——合并算法
当进行集合的合并时,即将两棵子树合并为一棵树,将一棵树的根节点指向另一颗子树的根节点;在合并时可按照子树的大小,将规模较小的子树合并到规模较大的子树上,从而使树更加平衡,从而优化未来查询的时间复杂度。
合并p所在的集合与q所在的集合:
查找p所在集合的根,i = find(p)
查找q所在集合的根,j = find(q)
如果i 与j 相同,则直接返回;
如果i 所在子树规模小于j 所在子树规模:
将i 的根指向 j ;
j 的规模增加i 子树的规模;
否则:
将j的根指向i ;
i 的规模增加j子树的规模;
子树个数减1
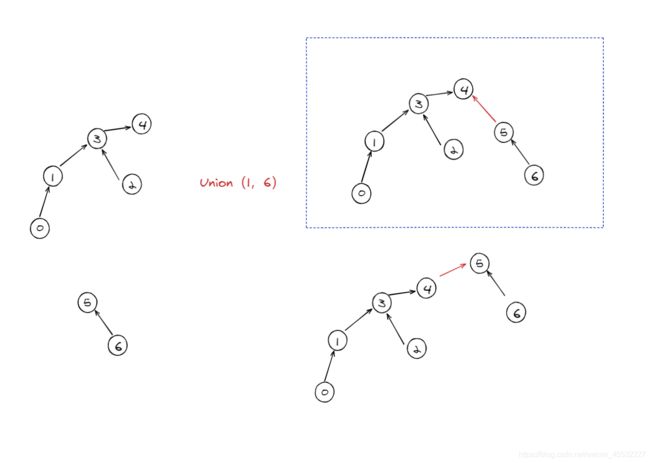
从上边可以看到,将规模较小的子树合并到规模较大的子树上,树更加平衡。
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot) return;
if(sz[pRoot] < sz[qRoot]) { id[pRoot] = qRoot; sz[qRoot] += sz[pRoot]; }
else { id[qRoot] = pRoot; sz[pRoot] += sz[qRoot]; }
count--;
}
整体代码
public class UnionFind {
private int[] id;
private int count;
private int[] sz;
public UnionFind(int N) {
count = N;
id = new int[N];
sz = new int[N];
for(int i = 0; i < N; i++) {
id[i] = i;
sz[i] = 1;
}
}
public int getCount() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int find(int p) {
if (p != id[p]) id[p] = find(id[p]);
return id[p];
}
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot) return;
if(sz[pRoot] < sz[qRoot]) { id[pRoot] = qRoot; sz[qRoot] += sz[pRoot]; }
else { id[qRoot] = pRoot; sz[pRoot] += sz[qRoot]; }
count--;
}
}