拔丝芋头的数据结构复习日记---Day2---堆栈、队列
< 今日知识点 >
- 堆栈
- 队列
·
·
·
—01 堆栈
1、栈的顺序存储实现
#define MAXSIZE //储存数据元素的最大个数
typedef struct SNode *Stack;
struct SNode{
ElementType Data[MAXSIZE];
int top;
};
- 栈的顺序存储结构通常由一个一维数组和一个记录栈顶元素位置的变量组成
- 当栈为空时，通常初始化栈顶元素位置变量top为-1
2、栈的操作实现
（1）入栈
void Push(Stack S,ElementType X)
{
if(S->top == MAXSIZE-1){
printf("堆栈满");
return ;
}else{
S->Data[++(S->top)] = X;
return ;
}
}
(2) 出栈
ElementType Pop(Stack S)
{
if(S->top == -1){
printf("堆栈空");
return Error; //ERROR是ElementType的特殊值，标志错误
} else {
return(S->Data[(S->top)--]);
}
}
例子：
-分析：一种比较聪明的方法是使这两个栈分别从数组的两头开始向中间生长，当两个栈的栈顶指针相遇时，就表示两个栈都满了
代码实现：
#define MAXSIZE <储存数据元素的最大个数>
struct DStack{
ElementType Data[MAXSIZE];
int top1;
int top2;
}S;
//初始化：
S.top==-1;
S.top2==MAXSIZE;
入栈操作：
void Push(struct DStack *S,ElementType item,int tag)
{
if（S->top2 - S->top1 == 1){
printf("堆栈已满");
return ;
}
if(tag==1) //对第一个堆栈进行操作
S->Data[++(S->top1)] = item;
else
S->Data[--(S->top2)] = item;
}出栈操作：
ElementType Pop(struct DStack *S,int tag)
{
if(tag==1){
if(S->top1==-1) {
printf("堆栈1空");
return NULL;
else return S->Data[(S->top1)--];
}else{
if(S->top2==MAXSIZE){
printf("堆栈2空");
return NULL;
else return S->Data[(S->top2)++];
}
}
- tag作为区分两个堆栈的标志，取值为1和2
3、堆栈的链式存储实现
typedef struct SNode *Stack;
struct SNode{
ElementType *Data;
struct SNode *Next;
};
- 栈的链式存储结构实际上就是一个单链表，叫做栈链。插入和删除操作只能在栈链的栈顶进行。
- 栈顶指针top应该在链表的哪一头？ （应该在链表头的位置）
4、栈的链式存储操作：
（1）堆栈初始化（建立空栈）
Stack CreateStack()
{
Stack S;
S = (Stack)malloc(sizeof(struct SNode));
S->Next = NULL;
return S;
}
- 即堆栈的一个头结点，返回指针
(2) 判断堆栈是否为空
int IsEmpty(Stack S)
{
return (S->Next == NULL)
- 判断堆栈是否为空，若为空返回整数1，否则返回0
（3） 入栈
void Push(ElementType item,Stack S)
{
struct SNode *TmpCell;
TmpCell = (struct SNode*)malloc(sizeof(struct SNode));
TmpCell->Element = item;
TmpCell->Next = S->Next;
S->Next = TmpCell;
}(4) 出栈
ElementType Pop(Stack S)
{ //删除并返回栈顶的元素
struct SNode *FirstCell;
ElementType topItem;
if(IsEmpty(S)){
printf("堆栈空");
return NULL;
}else {
FirstCell = S->Next;
S->Next = FirstCell -> Next;
topItem = FirstCell -> Element;
free(FirstCell);
return topItem;
}
}
5、堆栈应用：表达式求值
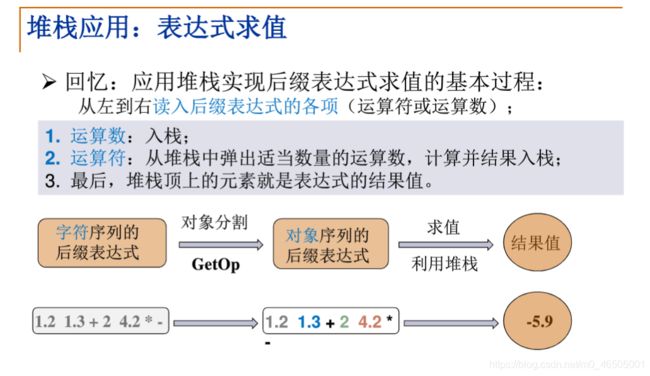
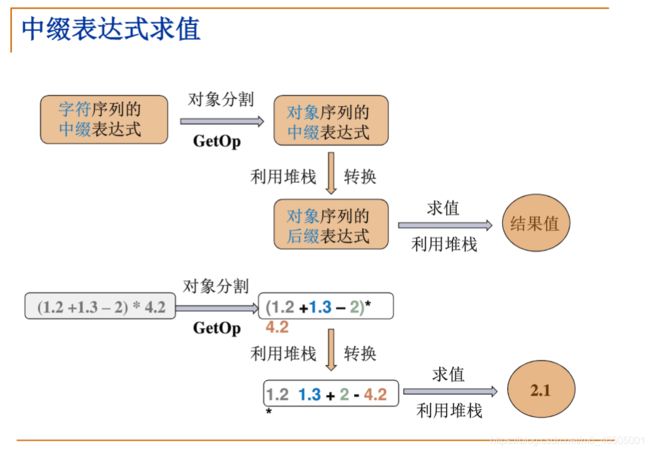
中缀表达式求值
基本策略：将中缀表达式转换为后缀表达式 （如何转换？）
观察一个简单例子：2+9 /3 -5 -> 2 9 3 / + 5 -
总结：
1、运算数相对顺序不变
2、运算符号顺序发生改变
- 需要存储等待中的运算符号
- 需要将当前运算符号与 等待中 的最后一个运算符 比较
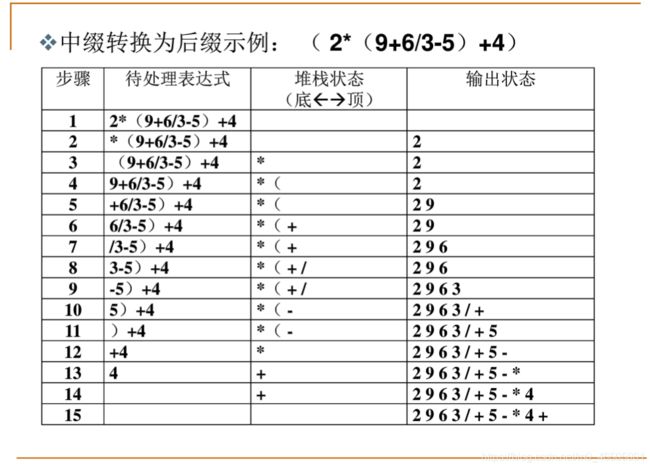
中缀表达式如何转换为后缀表达式
-----> 从头到尾读取中缀表达式的每个对象，对每个对象按不同的情况处理
1、运算数：直接输出
2、左括号：压入堆栈
3、右括号：将栈顶的运算符弹出并输出，直到遇到左括号（出栈，不输出）
4、运算符：
- 若优先级大于栈顶运算符时，则把它压栈
- 若优先级小于栈顶运算符时，将栈顶运算符弹出并输出。再比较新的栈顶运算符，直到运算符大于栈顶运算符优先级为止，然后将该运算符压栈。
5、若各对象处理完毕，则把堆栈中存留的运算符一并输出。
·
·
·
—02 队列
1、
代码：
#define MAXSIZE <储存数组元素的最大个数>
struct QNode{
ElementType Data[MAXSIZE];
int front;
int rear;
};
typedef struct QNode *Queue;
- 队列的顺序存储结构通常由一个一维数组和一个记录队列头元素位置的变量以及一个记录队尾元素位置的变量rear组成
2、 循环队列
思考题：
- 堆栈空的判别条件是front==rear ，堆栈满的判别条件是（rear+1）%MAXSIZE == 0
- 出现空、满无法区分的原因：堆栈可能出现的情况有七种，即空，和存在1、2、3、4、5、6个元素，而下标数字只有六种情况，即0~5，所以六个数字情况是无法不重复地表示堆栈的所有情况的，需要寻找新的表示方法
3、队列的操作
（1）入队列
void AddQ(Queue Q,ElementType item)
{
if(Q->rear+1)%MAXSIZE==Q->front){
printf("队列满");
return ;
}
Q->rear = (Q->rear+1）% MAXSIZE;
Q->Data[Q->rear] =item;
}
(2) 出队列
ElementType DeleteQ (Queue Q)
{
if(Q->front == Q->rear){
printf("队列空");
return ERROR；
}else{
Q->front = (Q->front+1)%MAXSIZE;
return Q->Data[Q->front];
}
}
- front和rear指针的移动采用 加1取余 法，体现了顺序存储的循环使用特性。
4、队列的链式存储实现
- 队列的链式存储结构也可以用一个单链表实现。插入和删除操作分别在链表的两头进行；
- 思考：队列指针front和rear应该分别指向链表的哪一头？？
- （front进行的是删除操作，应该指向链表头，rear进行的是插入操作，应该指向链表尾。因为对front来说，如果指向的是链表尾，那么一旦删除了一个元素，就找不到其他的元素了，即丢失了）
struct Node{
ElementType Data;
struct Node *Next;
};
struct QNode{ //链队列结构
struct Node *rear; //指向队尾和队头节点
struct Node *front;
}；
typedef struct QNode *Queue;
Queue Q;
- 不带头结点的链式队列出队操作的一个示例：
ElementType DeleteQ(Queue Q)
{
struct Node *frontCell;
ElementType frontElem;
if(Q->front ==NULL){
printf("队列空");
return ERROR;
}
frontCell = Q->front;
if(Q->front == Q->rear) //若队列中只有一个元素，删除后 队列置为空
Q->front = Q->rear =NULL;
else
Q->front = Q->front->Next;
frontElem = frontCell->Data;
free(frontCell);
return frontElem;
}
·
·
·
附：文中所有PPT图片均来自中国大学mooc 浙江大学《数据结构》课程！！