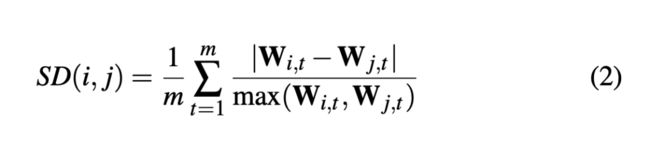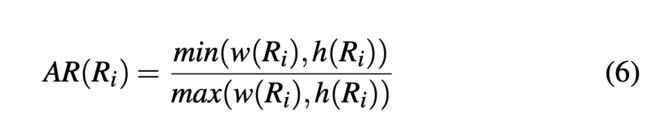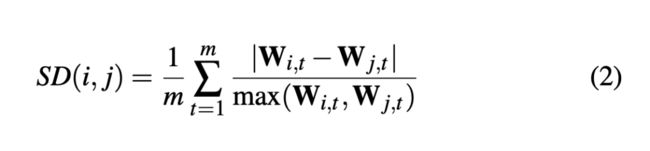可视化论文精读系列:SizePairs
论文题目:《SizePairs: Achieving Stable and Balanced Temporal Treemaps using Hierarchical Size-based Paring》
论文作者:Chang Han, Anyi Li, Jaemin Jo, Bongshin Lee, Oliver Deussen, Yunhai Wan
Treemap 简介
引用 http://www.tuzhidian.com:3000/chart?id=5c56e2434a8c5e048 189c6a5 的描述:
“树图,或者矩形树图,是一个由不同大小的嵌套式矩形来显示树状结构数据的统计图表。在矩形树图中,父子层级由矩形的嵌套表示。在同一层级中,所有矩形依次无间隙排布,他们的面积之和代表了整体的大小。单个矩形面积由其在同一层级的占比决定。”
本篇精读论文,主要介绍了时序treemap构建算法SizePairs,并设计了一系列实验与当前先进方法进行对比,证明了其能够生成美观且稳定的时序treemap布局,相关截图如无特别说明均来自论文。
算法目标
该算法的目标是快速生成稳定且平衡的treemap:
稳定:treemap在不同时间点应保持布局的稳定,每一项数据不会移动太多
平衡:各个矩形的长宽比比较平衡,尽可能美观(【2/3,1】的长宽比范围较为合适)
快速:算法耗时不能太长
论文中总结的算法设计目标如下:
• DG1. Create the layout of each time step as square as possible;
• DG2. Maintain the stability over time as much as possible; and
• DG3. Generate temporal treemaps as fast as possible.
算法思想
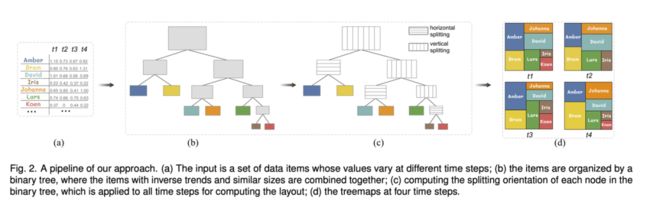
传统的treemap生成方法是不断对矩形进行递归划分,如下图(a,b,c):
若采用传统方法针对每一帧数据单独生成treemap布局,可以看到同一数据生成图形的位置变化较大,这在时序数据中很难用连贯且平滑的方式展现数据变化的过程。
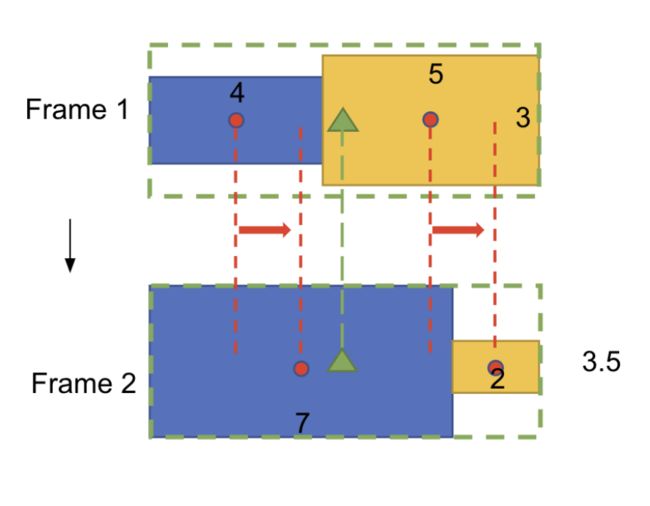
时序数据在变化过程中,变化趋势相反的数据项可以相互弥补:
上图展示了两个连续的时间帧中具有相反变化趋势的两个矩形。红色圆圈代表每个矩形的中心,绿色三角形代表整体布局的中心。可以看出当黄色矩形变小时,腾出的空间正好被蓝色矩形占满,从而使得整体中心保持不变。
将能够相互弥补的数据项放在一块,能够实现局部布局的稳定,从而实现整体布局的稳定效果。
采用层次打包配对的思想,不断寻找具有这种特性的数据项,将他们两两打包在一起。根据打包结果指导最终布局的生成。
同时,从全局的视角,而不仅仅是相邻的两个时间步对数据进行优化,能够取得更好的稳定性。
算法流程
输入数据
该算法针对的是时序(文本)数据,每一项数据在不同时间点都有不同的权重:
生成树构建
量化指标
Compensation Degree:衡量两个数据项i和j在所有时间步中相互弥补程度
在分子上,变化程度相反的两个数据项可以相互抵消,越小说明相互弥补的程度越好
Size Difference :衡量两个数据项i和j的差异程度
有些数据虽然相互弥补的程度很好,但是其长宽比差异过大,导致美观程度下降(b vs d)
因此定义了数据差异程度的量化指标:
该指标越小说明两个数据项越相似,将它们放在一块,可以避免极端情况的出现。
将上面两个指标结合,给i和j进行打分:
通过权重w在两项指标之间进行平衡,w=0.5 是一个推荐值。
层次打包
根据计算出的C(i,j),不断迭代,选择得分最优的两个数据项进行打包。打包后的两个数据项作为一个整体,参与下一轮迭代
(a)展示了传统的层次打包算法,每次选择得分最优的一对合并,并更新得分C(i,j)
为了避免极端情况的出现,规定面积大于所有矩形面积之和的2/3的矩形作为super nodes,并规定super nodes只能与super nodes相互打包。
打包算法流程
首先将所有数据项作为叶子节点,并计算相互之间的打包得分C(i,j)。首先将所有的super nodes移除,对所有的非super nodes进行迭代:每次选择得分最优的一对i j进行合并,再从剩下的非super nodes中选择得分最好的进行合并。不断重复直到无法合并为止。对所有新形成的节点,更新得分并挑出super nodes。不断重复,直到只剩下一个节点,或者没有节点剩余为止。
对于所有的super nodes,采用传统的层次打包算法,每次选择得分最优的一对合并,并更新得分C(i,j),直到只剩余一个节点为止。
打包算法伪代码
Treemap 布局生成
通过层次打包得到生成树之后,可以用来指导布局的生成
确定包内布局方向
采用每个数据项在所有时间步中的权重的中位数,作为其权重来对矩形进行划分。在水平与垂直划分之间,选择长宽比更优的一种划分方式。在每一帧中都保持这种划分方式,得到最终的treemap布局
可选项:针对每个时间步单独调整包内布局方向
为了进一步改善视觉效果,对于层次树中的倒数第二层的节点,在每个时间步中,针对水平与垂直两种划分方式,分别计算其里面的两个节点的长宽比a1,a2,并计算a1/a2,选择比值大于1.1的那种布局方式,作为在该时间步内的布局方式。
可以看做是一种局部调整。
最后得到了treemap的布局:
对交互的支持
删除/插入数据
对于删除/插入的数据,只需要将其后面/前面的时间步里面的权重设为0即可。sizePairs布局算法可以保持整体布局的稳定。
数据比较
若用户对两个数据项比较感兴趣,想对其进行对比。传统的treemap很难保证能将这两项数据放在一起进行比较。对于sizePairs,只需要将用户选择的两个数据项所对应的叶子节点打包在一起即可
标签友好
交互式的数据探索中往往会在treemap里引入标签。sizePairs可以得到一种分层的结构,允许通过调整父节点内两个子节点的布局方向,来完全兼容子节点的标签展示。
算法评价
评价指标
Corner-travel distance
对每个矩形,对于相邻的两个时间步,计算其Corner-travel distance并取平均值。
w(R),h(R)是整体布局的宽度,用来衡量short-term stability。
Normalized location drift
C(i,j)是矩形i在时间步j的中心,CoG(Ri)是所有时间步中矩形中心的平均值,用来衡量long-term stability。
Aspect ratio
矩形的长宽比,所有矩形所有时间步取平均值。
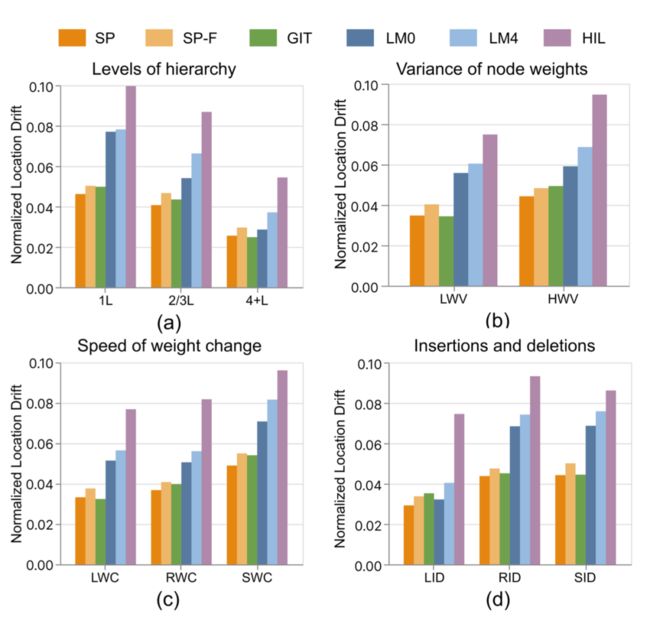
实验结果
从结果中我们可以看到,使用SizePairs 算法,各项指标都能得到一个比较好的结果。
几点思考
时序数据布局 统一的算法框架
抽象总结本文的算法框架,可以看出其采用时序数据变化过程中相互弥补保持稳定的思想,
先设定了两个优化目标:布局稳定性、美观程度
通过打包将能够相互弥补的两个数据放到一块,实现稳定性。在打包过程中,兼顾美观性
设计与稳定性、美观性相关量化指标,衡量两个数据项打包的好坏:
通过参数在多个指标间进行平衡
对于这种NP难的问题,采用启发式的层次打包方法,找出最优的打包方案,确定全局的布局
再设计了与美观性相关的度量指标,确定包内的布局,得到最终的布局结果
对于追求稳定性与美观性的时序数据可视化,都可以采用此算法框架。
例如,该算法可无缝应用到时序词云的布局中。
在时序词云中,主要追求高稳定性、低空白率与合适的长宽比
只需要将算法中的打分函数换成与词云稳定性相关的度量函数,根据空白率、长宽比确定包内的布局,采用完全相同的算法流程,就可以得到一个很好的时序词云布局,用来生成词云动画:
其他
历年VIS报告:https://www.youtube.com/c/IEEEVisualizationConference