重温四大基础数据结构:数组、链表、队列和栈
文章目录
- 前言
- 数组
- 链表
- 队列
- 栈
前言
数组、链表、队列、栈,是数据结构中最基础的四大结构,数组和链表更是基础中的基础,后续所有复杂的数据结构都是在它们的基础上演变而来的。
本节,我们就来重温这四大结构。
数组
关于数组,大家都比较熟悉了。
它是一种线性数据结构,使用一组连续的内存空间存储一组具有相同类型的数据。

这个概念中有三个关键词:线性、连续、相同类型。
线性,表示没有分叉,任意元素的前后元素最多只有一个,同样是线性结构的还有链表、队列等。
连续,它在内存空间中的存储是连续的,不间断的,前后两个元素紧挨着,不存在间隙。
相同类型,数组中存储的元素的类型一定是相同的,当然,在Java中,你可以使用Object代表所有类型,本质上,它们依然是相同类型。
正是有了上面三个特性,才使得数组具有了随机访问的特性,那么,什么是随机访问呢?
简单点说,你可以通过下标快速定位到数组中的元素,且时间复杂度是O(1),它是怎么做到的呢?
我们知道,计算机中只有0和1,一切的一切都可以看作是0和1的各种组合,内存也是一样。
当我们创建一个数组,比如int[] array = new int[]{2, 5, 8, 7};时,它其实返回的是这个数组在内存中的位置(地址),我们知道,一个int类型占用4个字节,也就是32位的0或1,当我们访问数组下标为0的元素时,直接返回数组地址处取32位转成int即可,同样地,当我们访问数组下标为1的元素时,返回数组地址加上(32*1)的地址处取32位转成int,依此类推。
这也是大部分语言中数组下标从0开始的原因,试想如果下标从1开始,那么,计算内存地址的时候就变成了address + 32 * (i - 1),这显然会造成一定的性能损耗。
链表
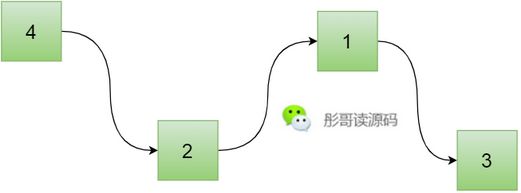
链表,它也是一种线程数据结构,与数组不同的是,它在内存空间中不一定是顺序存储的,为了保证链表中元素的连续性,一般使用一个指针来找到下一个元素。
上图是典型的单链表结构,在单链表中,只有一个指向下一个元素的指针。
如果要用Java类来表示单链表中的元素节点的话,大概看起来像这样子:
class Node {
int value;
Node next;
}
所以,链表不具有随机访问的特性,在链表中根据索引来查找元素只能从头开始(单链表),它的时间复杂度是O(n)。
上面我们说的是单链表,如果在单链表的基础上再增加一个前驱指针(指向前一个元素的指针),就变成了双向链表。

Java中的LinkedList就是典型的双向链表结构,双向链表既可以当作队列使用,又可以当作栈来使用,非常方便。
如果在双向链表的基础上再增加HashMap的功能,就变成了LinkedHashMap了,咳咳,扯远了。
希望学习LinkedList和LinkedHashMap源码解析的同学,可以关注我的公号主“彤哥读源码”。
这里提到了队列,那么,什么是队列呢?
队列
所谓队列,其实跟现实中的排队是一样的,其中的元素从一端进入,从另一端出去,英文叫做:First In,First Out,简写FIFO。
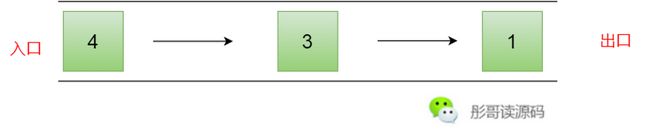
从这张图,也可以看出来,实现队列最简单的方式就是使用链表,把上图中的箭头倒过来即可。
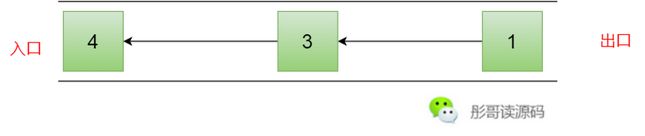
入队时,将元素加入到链表尾端,出队时,将第一个元素删除并将头节点指向下一个节点即可。
让我们来看看使用链表实现队列的简单代码实现:
public class LinkedQueue {
Node head;
Node tail;
void offer(Integer value) {
if (value == null) {
throw new NullPointerException();
}
Node node = new Node(value);
if (head == null) {
head = tail = node;
} else {
tail.next = node;
tail = node;
}
}
Integer poll() {
Node first = head;
if (first != null) {
head = first.next;
first.next = null;
return first.value;
} else {
return null;
}
}
static class Node {
int value;
Node next;
public Node(int value) {
this.value = value;
}
}
}
是不是很简单呢?
那么,数组能不能实现队列呢?
答案是肯定的,使用数组实现队列有很多种方式,其中一种是使用两个指针:入指针、出指针,它们分别指向下一个入队列和下一个出队列的位置。
入队时,在入指针处放入元素,同时入指针后移。
出队时,取出出指针处的元素返回,同时出指针后移。
当指针到达数组末尾时,返回数组开始的位置。
此时,我们考虑一个问题,队列空和队列满时,两个指针都是指向同一个位置,似乎不太好处理。
其实,很简单,引入一个size变量标识队列中有多少个元素即可。
所以,这玩意儿要怎么实现呢?Show me the code!
public class ArrayQueue {
int[] array;
int offerIndex;
int pollIndex;
int size;
public ArrayQueue(int capacity) {
this.array = new int[capacity];
this.offerIndex = this.pollIndex = 0;
this.size = 0;
}
boolean offer(Integer value) {
if (value == null) {
throw new NullPointerException();
}
if (size == array.length) {
return false;
}
array[offerIndex] = value;
offerIndex = (offerIndex + 1) % array.length;
size++;
return true;
}
Integer poll() {
if (size == 0) {
return null;
}
int value = array[pollIndex];
pollIndex = (pollIndex + 1) % array.length;
size--;
return value;
}
}
OK,以上就是使用数组实现的队列,可以看到,与链表实现的队列相比,它需要指定容量,这叫做有界队列,如果需要使用数组实现无界队列,则需要加入扩容的机制,有兴趣的同学可以自己实现看看。
下面,我们再来看另一种基础的数据结构——栈。
栈
栈,它是与队列表现完全相反的数据结构,它的元素是先进的后出来,就像我们往一个杯子里面放东西一样,先放进去的放在最下面,只有把上面的东西拿出来后才能拿出下面压着的东西,这种行为用英文叫做:First In,Last Out,简称FILO。
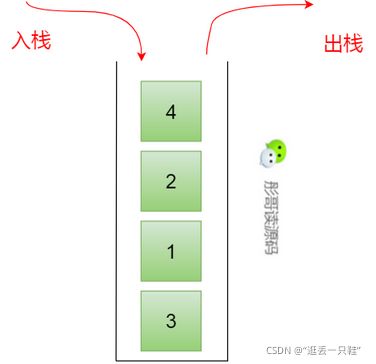
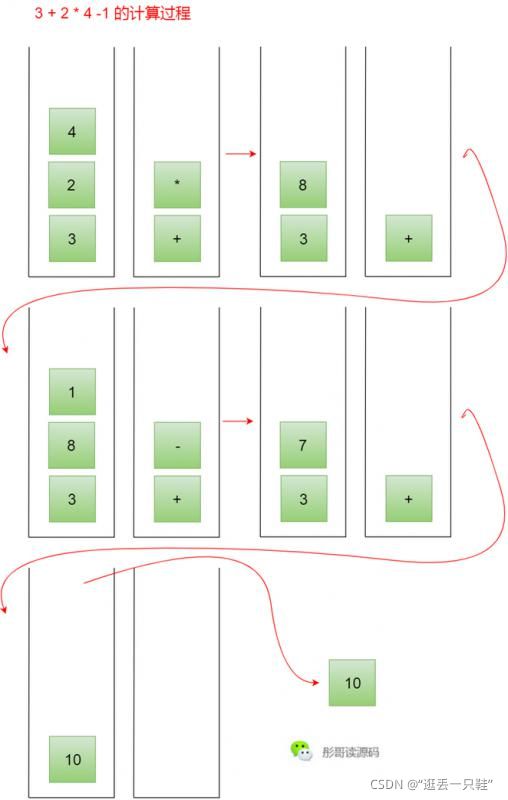
栈,具有很多用处,计算机中很多处理都是通过栈这种数据结构来进行的,比如算术运算,准备两个栈,一个栈存储数字,一个栈存储符号,从头开始依次把字符压入到这两个栈中,当遇到符号优先级比栈顶元素低时,则取出栈顶符号,并从数字栈中取出两个数字进行运算,运算的结果再压回数字栈中,继续以此运行,当所有字符都放入栈之后,依次从数字栈中取出两个元素,并从符号栈中取出一个元素,进行计算,结果压回数字栈,继续以此运行,直到符号栈为空,或者数字栈只剩下一个元素为止,弹出这个数字即为最后的结果。
好了,关于栈,我们就简单介绍到这里,后面,我们还会大量遇到这个数据结构。