初阶数据结构——顺序表和链表(单链表)
目录
-
- 1.线性表
- 2.顺序表
-
- SeqList.h
- SeqList.c
- Test.c
- 数组习题
-
- 移除元素
- 删除有序数组中的重复项
- 合并两个有序数组
- 顺序表的问题及思考
- 3.链表
-
- SList.h
- SList.c
- Test.c
- CPU缓存相关拓展
- 链表和顺序表的优缺点
1.线性表
线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使
用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构,也就说是连续的一条直线。但是在物理结构上并不一定是连续的,
线性表在物理上存储时,通常以数组和链式结构的形式存储
2.顺序表
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存
储。在数组上完成数据的增删查改。
顺序表一般可以分为:
1、静态顺序表:使用定长数组存储元素。
2、动态顺序表:使用动态开辟的数组存储。
主要介绍动态
SeqList.h
#pragma once
#includeSeqList.c
void SLInit(SL* psl)
{
assert(psl);
psl->a = (SLDatatype*)malloc(sizeof(SLDatatype)*4);
if (psl->a == NULL)
{
perror("malloc fail");
return;
}
psl->capacity = 4;
psl->size = 0;
}
void SLDestroy(SL* psl)
{
assert(psl);
free(psl->a);
psl->a = NULL;
psl->size = 0;
psl->capacity = 0;
}
void SLPrint(SL* psl)
{
assert(psl);
for (int i = 0; i < psl->size; i++)
{
printf("%d ", psl->a[i]);
}
printf("\n");
}
void SLCheckCapacity(SL* psl)
{
assert(psl);
if (psl->size == psl->capacity)
{
SLDatatype* tmp = (SLDatatype*)realloc(psl->a, sizeof(SLDatatype) * psl->capacity * 2);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
psl->a = tmp;
psl->capacity *= 2;
}
}
void SLPushBack(SL* psl, SLDatatype x)
{
assert(psl);
//psl->a[psl->size] = x;
//psl->size++;
//SLCheckCapacity(psl);
//psl->a[psl->size++] = x;
SLInsert(psl, psl->size, x);
}
void SLPushFront(SL* psl, SLDatatype x)
{
assert(psl);
//SLCheckCapacity(psl);
挪动数据
//int end = psl->size - 1;
//while (end >= 0)
//{
// psl->a[end + 1] = psl->a[end];
// --end;
//}
//psl->a[0] = x;
//psl->size++;
SLInsert(psl, 0, x);
}
void SLPopBack(SL* psl)
{
assert(psl);
// 暴力检查
//assert(psl->size > 0);
温柔的检查
if (psl->size == 0)
return;
psl->a[psl->size - 1] = 0;
//psl->size--;
SLErase(psl, psl->size-1);
}
void SLPopFront(SL* psl)
{
assert(psl);
// 暴力检查
//assert(psl->size > 0);
///*int start = 0;
//while (start < psl->size-1)
//{
// psl->a[start] = psl->a[start + 1];
// start++;
//}*/
//int start = 1;
//while (start < psl->size)
//{
// psl->a[start-1] = psl->a[start];
// start++;
//}
//psl->size--;
SLErase(psl, 0);
}
void SLInsert(SL* psl, int pos, SLDatatype x)
{
assert(psl);
//assert(0 <= pos <= psl->size);
assert(0 <= pos && pos<= psl->size);
SLCheckCapacity(psl);
int end = psl->size - 1;
while (end >= pos)
{
psl->a[end + 1] = psl->a[end];
--end;
}
psl->a[pos] = x;
psl->size++;
}
void SLErase(SL* psl, int pos)
{
assert(psl);
assert(0 <= pos && pos < psl->size);
//assert(psl->size > 0);
int start = pos + 1;
while (start < psl->size)
{
psl->a[start - 1] = psl->a[start];
++start;
}
psl->size--;
}
int SLFind(SL* psl, SLDatatype x)
{
assert(psl);
for (int i = 0; i < psl->size; i++)
{
if (psl->a[i] == x)
{
return i;
}
}
return -1;
}
void SLModify(SL* psl, int pos, SLDatatype x)
{
assert(psl);
assert(0 <= pos && pos < psl->size);
psl->a[pos] = x;
}
Test.c
注意:如果scanf()函数使用的是%d转换说明符,那么当程序读取的第一个字符为非数字字符比如‘A’时,scanf()将会读取失败,‘A’会待在缓冲区,所以得先清空缓冲区才能让scanf继续读取
void menu()
{
printf("***************************************\n");
printf("1、尾插数据 2、尾删数据\n");
printf("3、头插数据 4、头删数据\n");
printf("5、打印数据 -1、退出\n");
printf("***************************************\n");
}
int main()
{
int option = 0;
SL s;
SLInit(&s);
while (option != -1)
{
menu();
printf("请输入你的操作:>");
scanf("%d", &option);
if (option == 1)
{
/*printf("请输入要尾插的数据,以-1结束:");
int x = 0;
scanf("%d", &x);
while (x != -1)
{
SLPushBack(&s, x);
scanf("%d", &x);
}*/
int n = 0;
printf("请输入要尾插的数据个数,再依次输入要插入的数据:");
scanf("%d", &n);
int x = 0;
while (n > 0)
{
scanf("%d", &x);
SLPushBack(&s, x);
n--;
}
}
else if (option == 5)
{
SLPrint(&s);
}
else if (option == -1)
{
break;
}
else
{
printf("无此选项,请重新输入\n");
}
}
SLDestroy(&s);
return 0;
}
数组习题
移除元素
int removeElement(int* nums, int numsSize, int val){
int pos=0,prev=0;
for(int i=0;i<numsSize;i++)
{
if(nums[pos]==val)
{
pos++;
}
else
{
nums[prev++]=nums[pos++];
}
}
return prev;
}
删除有序数组中的重复项
int removeDuplicates(int* nums, int numsSize){
int pos=0,prev=0;
while(pos<numsSize)
{
if(nums[pos]==nums[prev])
{
pos++;
}
else
{
prev++;
nums[prev]=nums[pos];
}
}
return prev+1;
}
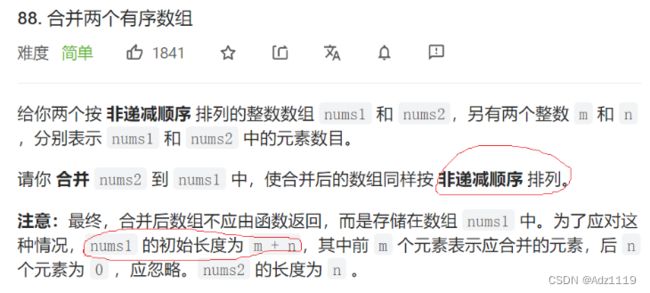
合并两个有序数组
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
//归并,从后往前比较,放到nums1中
int len1=m-1;
int len2=n-1;
int k=m+n-1;
while(len1>=0 && len2>=0)
{
if(nums1[len1]>nums2[len2])
{
nums1[k--]=nums1[len1--];
}
else
{
nums1[k--]=nums2[len2--];
}
}
while(len2>=0)
{
nums1[k--]=nums2[len2--];
}
}
顺序表的问题及思考
顺序表优势:下标的随机访问
问题:
- 中间/头部的插入删除,时间复杂度为O(N)
- 增容需要申请新空间,拷贝数据,释放旧空间。会有不小的消耗。
- 增容一般是呈2倍的增长,势必会有一定的空间浪费。例如当前容量为100,满了以后增容到
200,我们再继续插入了5个数据,后面没有数据插入了,那么就浪费了95个数据空间。
3.链表
概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。
双向链表的实现可以看:带头双向循环链表
SList.h
#pragma once
#includeSList.c
void SLTPrint(SLTNode* phead)
{
SLTNode* cur = phead;
while (cur != NULL)
{
printf("%d->", cur->data);
cur = cur->next;
}
printf("NULL\n");
}
SLTNode* BuyLTNode(SLTDataType x)
{
SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
void SLPushFront(SLTNode** pphead, SLTDataType x)
{
assert(pphead); // 链表为空,pphead也不为空,因为他是头指针plist的地址
//assert(*pphead); // 不能断言,链表为空,也需要能插入
SLTNode* newnode = BuyLTNode(x);
newnode->next = *pphead;
*pphead = newnode;
}
//void SLPushBack(SLTNode* phead, SLTDataType x)
//{
// SLTNode* tail = phead;
// while (tail != NULL)
// {
// tail = tail->next;
// }
//
// SLTNode* newnode = BuyLTNode(x);
// tail = newnode;
//}
void SLPushBack(SLTNode** pphead, SLTDataType x)
{
assert(pphead); // 链表为空,pphead也不为空,因为他是头指针plist的地址
//assert(*pphead); // 链表为空,可以尾插
SLTNode* newnode = BuyLTNode(x);
// 1、空链表
// 2、非空链表
if (*pphead == NULL)
{
*pphead = newnode;
}
else
{
SLTNode* tail = *pphead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newnode;
}
}
void SLPopFront(SLTNode** pphead)
{
assert(pphead); // 链表为空,pphead也不为空,因为他是头指针plist的地址
assert(*pphead); // 链表为空,不能头删。(当然你还可以用温柔的检查)
SLTNode* del = *pphead;
*pphead = (*pphead)->next;
free(del);
// 一个节点
// 多个节点
//if ((*pphead)->next == NULL)
//{
// free(*pphead);
// *pphead = NULL;
//}
//else
//{
// SLTNode* del = *pphead;
// //*pphead = del->next;
// *pphead = (*pphead)->next;
// free(del);
//}
}
void SLPopBack(SLTNode** pphead)
{
assert(pphead); // 链表为空,pphead也不为空,因为他是头指针plist的地址
assert(*pphead); // 链表为空,不能头删。(当然你还可以用温柔的检查)
// 没有节点(空链表)
// 暴力检查
//assert(*pphead);
// 温柔的检查
/*if (*pphead == NULL)
{
return;
}*/
// 一个节点
// 多个节点
if ((*pphead)->next == NULL)
{
free(*pphead);
*pphead = NULL;
}
else
{
//SLTNode* prev = NULL;
//SLTNode* tail = *pphead;
找尾
//while (tail->next)
//{
// prev = tail;
// tail = tail->next;
//}
//free(tail);
//prev->next = NULL;
SLTNode* tail = *pphead;
// 找尾
while (tail->next->next)
{
tail = tail->next;
}
free(tail->next);
tail->next = NULL;
}
}
SLTNode* STFind(SLTNode* phead, SLTDataType x)
{
//assert(phead);
SLTNode* cur = phead;
while (cur)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
// 在pos之前插入
void SLInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
assert(pphead);
assert(pos);
//assert(*pphead);
if (*pphead == pos)
{
SLPushFront(pphead, x);
}
else
{
SLTNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
}
SLTNode* newnode = BuyLTNode(x);
prev->next = newnode;
newnode->next = pos;
}
}
// 在pos之后插入
void SLInsertAfter(SLTNode* pos, SLTDataType x)
{
assert(pos);
SLTNode* newnode = BuyLTNode(x);
newnode->next = pos->next;
pos->next = newnode;
}
// 删除pos位置的值
void SLErase(SLTNode** pphead, SLTNode* pos)
{
assert(pphead);
assert(pos);
if (pos == *pphead)
{
SLPopFront(pphead);
}
else
{
SLTNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = pos->next;
free(pos);
}
}
void SLEraseAfter(SLTNode* pos)
{
assert(pos);
assert(pos->next);
SLTNode* next = pos->next;
pos->next = next->next;
free(next);
}
Test.c
void TestSList4()
{
SLTNode* plist = NULL;
SLPushBack(&plist, 1);
SLPushBack(&plist, 2);
SLPushBack(&plist, 3);
SLPushBack(&plist, 4);
SLTPrint(plist);
SLTNode* pos = STFind(plist, 3);
if (pos)
{
SLInsert(&plist, pos, 30);
}
SLTPrint(plist);
pos = STFind(plist, 2);
if (pos)
{
SLInsertAfter(pos, 20);
}
SLTPrint(plist);
pos = STFind(plist, 2);
if (pos)
{
SLErase(&plist, pos);
}
SLTPrint(plist);
}
int main()
{
TestSList4();
return 0;
}
CPU缓存相关拓展
数据结构是在内存中管理数据。
内存(主存)是带电存储,而磁盘是不带电存储,要永久保存的数据就放到磁盘,要快速访问就在内存。
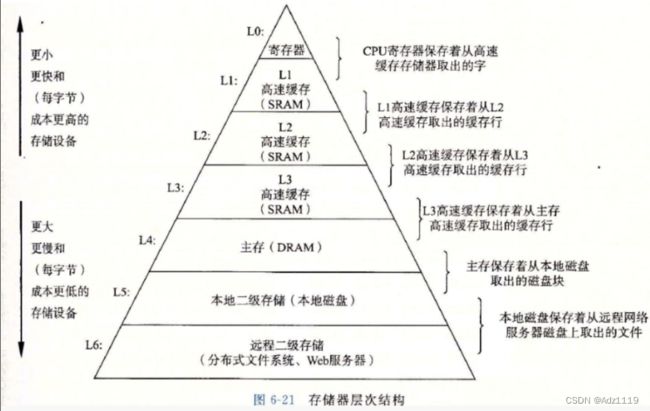
我们要读取数据的时候本质是cpu去访问,cpu不会直接地去访问内存,因为cpu相比内存来说太快,cpu和内存中间存在着两类介质,一个是三级高速缓存,一个是寄存器,如果数据量较少那么会放到寄存器,寄存器很快但它的数量有限。当cpu要访问数据,可以先放到寄存器,cpu去访问寄存器。

int i=0; ++i时可以看出不是直接对内存进行add,而是把i放到寄存器然后对寄存器add。

当访问顺序表链表时,一般是属于大数据,就会往缓存放,这时候会涉及到缓存命中的问题:先看这个数据是否在缓存,在就叫缓存命中,则直接访问。如果不在就是不命中,就先加载数据到缓存,再访问
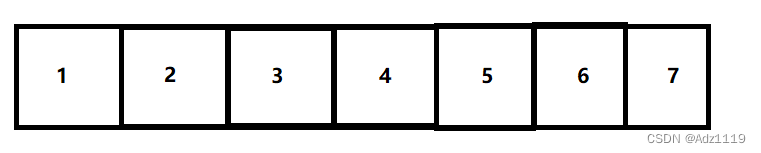
由于硬件的原因,访问图中这个位置的数据时,这个数据只有4/8字节,不会只加载这个数据(为了效率),会加载这部分数据及其后面的一段,加载的长度和硬件有关,一般会加载一个cpu的字长。
加载一长段而不是只加载当前一段的原因有:由于硬件设计等等原因,加载当前一段和加载一长段的成本基本相同,更重要的一个原因是局部性原理:CPU访问 存储器 时,无论是存取指令还是存取数据,所访问的 存储单元 都趋于聚集在一个较小的连续区域中。 时间局部性(Temporal Locality):如果一个信息项正在被访问,那么在近期它很可能还会被再次访问。

当第一个位置不命中,会加载一长段数据到缓存,顺序表和链表都会加载,不一样的是当我们访问第二个部分,顺序表会命中,因为它的物理空间是连续的。对于链表而言,第二个部分命中的概率就小了,因为链表节点是malloc的,地址之间没有关联。
不命中同时还会有缓存污染,(把不用的数据加载到缓存)缓存的大小是有限的,把链表1加载过去(加载了二十字节过去,但只有4字节是需要的,别的16字节不知道是什么,大概率是我们不需要的数据),不仅不命中还让不需要的数据占用了空间,如果缓存里的空间已经满了,就会把最近没有被访问的换出去。链表前后加载了八十字节,而顺序表只加载了二十字节。
从频繁访问数据来说顺序表的效率会比链表高,因为物理空间连续
如果大量头部挪动数据,那么链表效率高