初级数据结构——栈和队列
目录
-
- 1.栈
-
- 栈的概念及结构
- 栈的实现
- 栈的结构
- 初始化栈
- 入栈
- 出栈
- 获取栈顶元素
- 获取栈中有效元素个数
- 检测栈是否为空
- 销毁栈
- Stack.h
- Stack.c
- Test.c
- 2.队列
-
- 队列的概念及结构
- 队列的实现
- 队列的结构
- 初始化队列
- 队尾入队列
- 队头出队列
- 获取队列头部元素
- 获取队列队尾元素
- 获取队列中有效元素个数
- 检测队列是否为空
- 销毁队列
- Queue.h
- Queue.c
1.栈
栈的概念及结构
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
栈的实现
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小,cpu缓存命中率更高。
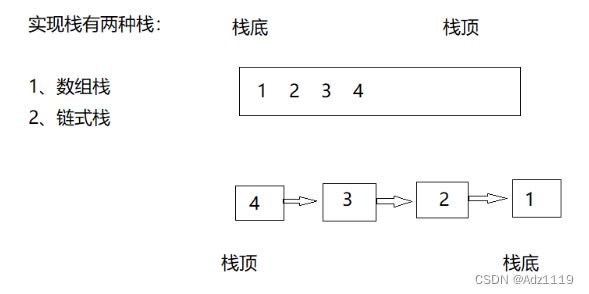
因为栈和队列的性质,所以就不写print函数打印栈,栈出数据就只能后进先出,取栈顶元素,然后出栈
栈的结构
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
初始化栈
void STInit(ST* pst)
{
assert(pst);
pst->a = NULL;
//pst->top = -1; // top 指向栈顶数据
pst->top = 0; // top 指向栈顶数据的下一个位置
pst->capacity = 0;
}
对top的赋值要注意top的指向
如果top初始值为0,那么赋值时pst->a[pst->top++]=x
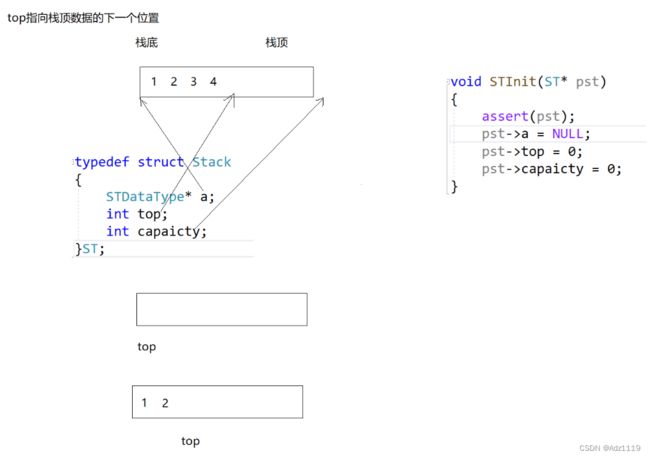
如果top初始值为-1,那么赋值时pst->a[++pst->top]=x

入栈
void STPush(ST* pst, STDataType x)
{
if (pst->top == pst->capacity)
{
int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->a, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
pst->a = tmp;
pst->capacity = newCapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
出栈
void STPop(ST* pst)
{
assert(pst);
assert(!STEmpty(pst));
pst->top--;
}
获取栈顶元素
STDataType STTop(ST* pst)
{
assert(pst);
assert(!STEmpty(pst));
return pst->a[pst->top - 1];
}
写获取栈顶元素的函数是有必要的,如果想通过结构体直接访问结构体中数据,是不好的,(容易写错)比如:ST st; st.a[st.top](错误的写法) 这样使用的人成本高,因为他不知道top是指向栈顶元素还是指向栈顶元素的下一个位置,还得很熟悉栈,不熟悉的人看到top初始化的时候是0会以为top就是栈顶元素,然后st.a[st.top]得了个随机值。
获取栈中有效元素个数
int STSize(ST* pst)
{
assert(pst);
return pst->top;
}
检测栈是否为空
bool STEmpty(ST* pst)
{
assert(pst);
/*if (pst->top == 0)
{
return true;
}
else
{
return false;
}*/
return pst->top == 0;
}
销毁栈
void STDestroy(ST* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
Stack.h
#pragma once
#includeStack.c
#include "Stack.h"
void STInit(ST* pst)
{
assert(pst);
pst->a = NULL;
//pst->top = -1; // top 指向栈顶数据
pst->top = 0; // top 指向栈顶数据的下一个位置
pst->capacity = 0;
}
void STDestroy(ST* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
void STPush(ST* pst, STDataType x)
{
if (pst->top == pst->capacity)
{
int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->a, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
pst->a = tmp;
pst->capacity = newCapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
void STPop(ST* pst)
{
assert(pst);
assert(!STEmpty(pst));
pst->top--;
}
STDataType STTop(ST* pst)
{
assert(pst);
assert(!STEmpty(pst));
return pst->a[pst->top - 1];
}
bool STEmpty(ST* pst)
{
assert(pst);
/*if (pst->top == 0)
{
return true;
}
else
{
return false;
}*/
return pst->top == 0;
}
int STSize(ST* pst)
{
assert(pst);
return pst->top;
}
Test.c
因为栈和队列的性质,所以就不写print函数打印栈,栈出数据就只能后进先出,取栈顶元素,然后出栈
void TestStack1()
{
ST st;
STInit(&st);
STPush(&st, 1);
STPush(&st, 2);
printf("%d ", STTop(&st));
STPop(&st);
STPush(&st, 3);
STPush(&st, 4);
while (!STEmpty(&st))
{
printf("%d ", STTop(&st));
STPop(&st);
}
STDestroy(&st);
}
int main()
{
TestStack1();
return 0;
}
2.队列
队列的概念及结构
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 的原则
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头

队列的实现
队列的结构
要定义两个结构
一个是节点,因为要组成链表,然后看单链表能不能解决问题,如果不能则用双向链表,这里用单链表就可以。
另一个结构是两个指针和记录个数的size,因为,在队尾插入,队头删除,需要两个指针,还需要一个size,不要size也可以,但是当我们需要个数的时候就要遍历才能获取(效率就低了),在栈的实现中可以通过top获取个数也就不需要size。
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
}QNode;
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;
初始化队列
设计函数的时候不需要二级指针,比如在插入的时候需要改变头尾指针,但是我们不是直接传的头尾指针,头尾指针是放在结构体Queue中的,要改变结构体中的成员,可以通过结构体指针。
void QueueInit(Queue* pq)
{
assert(pq);
pq->phead = NULL;
pq->ptail = NULL;
pq->size = 0;
}
队尾入队列
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail\n");
return;
}
newnode->data = x;
newnode->next = NULL;
if (pq->ptail == NULL)
{
assert(pq->phead == NULL);
pq->phead = pq->ptail = newnode;
}
else
{
pq->ptail->next = newnode;
pq->ptail = newnode;
}
pq->size++;
}
队头出队列
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
// 1、一个节点
// 2、多个节点
if (pq->phead->next == NULL)
{
free(pq->phead);
pq->phead = pq->ptail = NULL;
}
else
{
// 头删
QNode* next = pq->phead->next;
free(pq->phead);
pq->phead = next;
}
pq->size--;
}
获取队列头部元素
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->phead->data;
}
获取队列队尾元素
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->ptail->data;
}
获取队列中有效元素个数
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
检测队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
/*return pq->phead == NULL
&& pq->ptail == NULL;*/
return pq->size == 0;
}
销毁队列
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
Queue.h
#includeQueue.c
void QueueInit(Queue* pq)
{
assert(pq);
pq->phead = NULL;
pq->ptail = NULL;
pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail\n");
return;
}
newnode->data = x;
newnode->next = NULL;
if (pq->ptail == NULL)
{
assert(pq->phead == NULL);
pq->phead = pq->ptail = newnode;
}
else
{
pq->ptail->next = newnode;
pq->ptail = newnode;
}
pq->size++;
}
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
// 1、一个节点
// 2、多个节点
if (pq->phead->next == NULL)
{
free(pq->phead);
pq->phead = pq->ptail = NULL;
}
else
{
// 头删
QNode* next = pq->phead->next;
free(pq->phead);
pq->phead = next;
}
pq->size--;
}
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->ptail->data;
}
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
/*return pq->phead == NULL
&& pq->ptail == NULL;*/
return pq->size == 0;
}
