【Matlab】智能优化算法_遗传算法GA

1.背景介绍

遗传算法（Genetic Algorithm，简称GA）是一种基于生物进化理论的优化算法，由John Holland于20世纪70年代初提出。它通过模拟自然选择和遗传机制，利用群体中个体之间的遗传信息交流和变异来搜索问题的解空间。

遗传算法的设计灵感来源于达尔文的进化论。达尔文提出，自然界中的生物通过遗传信息的传递和变异，逐步适应环境并进化。类似地，遗传算法通过对问题解空间中的个体进行选择、交叉和变异操作，模拟了生物进化的过程，以寻找问题的最优解或次优解。

2.数学模型

遗传算法的核心思想是通过不断迭代的过程，从初始的随机个体群体出发，通过选择、交叉和变异操作产生新一代的个体群体，使得群体中的个体逐渐适应环境并优化问题的目标函数。具体而言，遗传算法的步骤如下：

1. 初始化：随机生成初始的个体群体，代表解空间中的潜在解。
2. 评估：根据问题的目标函数，对每个个体进行评估，计算其适应度值，表示解的优劣程度。
3. 选择：根据适应度值，选择优秀的个体作为父代，用于产生下一代的个体。选择策略可以是轮盘赌选择、竞争选择等。
4. 交叉：从父代个体中选取一对个体，通过交叉操作产生新的个体，将两个个体的染色体信息进行混合。
5. 变异：对新生成的个体进行变异操作，引入随机性，增加搜索空间的多样性。
6. 更新：用新生成的个体替换原有的个体群体，形成下一代个体群体。
7. 终止条件：通过设定的终止条件，如达到最大迭代次数、目标函数值达到一定阈值等，判断算法是否停止。
8. 返回最优解：遗传算法迭代完成后，返回适应度值最高的个体作为问题的解。

遗传算法具有全局搜索能力、自适应性和鲁棒性，适用于各种优化问题，尤其在复杂、多模态和高维的问题中表现出色。它在工程、运筹学、人工智能等领域都有广泛应用，并衍生出许多变种算法和改进方法，如遗传编程、进化策略等。

3.文件结构

crossover.m						% 交叉育种
elitism.m						% 精英化
GeneticAlgorithm.m				% 遗传算法
initialization.m				% 初始化
Main.m							% 主函数
mutation.m						% 变异
selection.m						% 选择
Sphere.m						% 

4.详细代码及注释

4.1 crossover.m

function [child1 , child2] = crossover(parent1 , parent2, Pc, crossoverName)

switch crossoverName
    case 'single'
        Gene_no = length(parent1.Gene);
        ub = Gene_no - 1;
        lb = 1;
        Cross_P = round (  (ub - lb) *rand() + lb  );
        
        Part1 = parent1.Gene(1:Cross_P);
        Part2 = parent2.Gene(Cross_P + 1 : Gene_no);
        child1.Gene = [Part1, Part2];
        
        Part1 = parent2.Gene(1:Cross_P);
        Part2 = parent1.Gene(Cross_P + 1 : Gene_no);
        child2.Gene = [Part1, Part2];
        
        
    case 'double'
        Gene_no = length(parent1);
       
        ub = length(parent1.Gene) - 1;
        lb = 1;
        Cross_P1 = round (  (ub - lb) *rand() + lb  );
        
        Cross_P2 = Cross_P1;
        
        while Cross_P2 == Cross_P1
            Cross_P2 = round (  (ub - lb) *rand() + lb  );
        end
        
        if Cross_P1 > Cross_P2
            temp =  Cross_P1;
            Cross_P1 =  Cross_P2;
            Cross_P2 = temp;
        end

        Part1 = parent1.Gene(1:Cross_P1);
        Part2 = parent2.Gene(Cross_P1 + 1 :Cross_P2);
        Part3 = parent1.Gene(Cross_P2+1:end);
        
        child1.Gene = [Part1 , Part2 , Part3];
        
        
        Part1 = parent2.Gene(1:Cross_P1);
        Part2 = parent1.Gene(Cross_P1 + 1 :Cross_P2);
        Part3 = parent2.Gene(Cross_P2+1:end);
        
        child2.Gene = [Part1 , Part2 , Part3];
end

R1 = rand();

if R1 <= Pc
    child1 = child1;
else
    child1 = parent1;
end

R2 = rand();

if R2 <= Pc
    child2 = child2;
else
    child2 = parent2;
end

end

4.2 elitism.m

function [ newPopulation2 ] = elitism(population , newPopulation, Er)

M = length(population.Chromosomes); % number of individuals 
Elite_no = round(M * Er);

[max_val , indx] = sort([ population.Chromosomes(:).fitness ] , 'descend');
    
% The elites from the previous population
for k = 1 : Elite_no
    newPopulation2.Chromosomes(k).Gene  = population.Chromosomes(indx(k)).Gene;
    newPopulation2.Chromosomes(k).fitness  = population.Chromosomes(indx(k)).fitness;
end

% The rest from the new population
for k = Elite_no + 1 :  M
    newPopulation2.Chromosomes(k).Gene  = newPopulation.Chromosomes(k).Gene;
    newPopulation2.Chromosomes(k).fitness  = newPopulation.Chromosomes(k).fitness;
end

end

4.3 GeneticAlgorithm.m

function [BestChrom]  = GeneticAlgorithm (M , N, MaxGen , Pc, Pm , Er , obj, visuailzation)

cgcurve = zeros(1 , MaxGen);

%%  Initialization
[ population ] = initialization(M, N);
for i = 1 : M
    population.Chromosomes(i).fitness = obj( population.Chromosomes(i).Gene(:) );
end

g = 1;
disp(['Generation #' , num2str(g)]);
[max_val , indx] = sort([ population.Chromosomes(:).fitness ] , 'descend');
cgcurve(g) = population.Chromosomes(indx(1)).fitness;

%% Main loop
for g = 2 : MaxGen
    disp(['Generation #' , num2str(g)]);
    % Calcualte the fitness values
    for i = 1 : M
        population.Chromosomes(i).fitness = Sphere( population.Chromosomes(i).Gene(:) );
    end
    
    for k = 1: 2: M
        % Selection
        [ parent1, parent2] = selection(population);
        
        % Crossover
        [child1 , child2] = crossover(parent1 , parent2, Pc, 'single');
        
        % Mutation
        [child1] = mutation(child1, Pm);
        [child2] = mutation(child2, Pm);
        
        newPopulation.Chromosomes(k).Gene = child1.Gene;
        newPopulation.Chromosomes(k+1).Gene = child2.Gene;
    end
    
    for i = 1 : M
        newPopulation.Chromosomes(i).fitness = obj( newPopulation.Chromosomes(i).Gene(:) );
    end
    % Elitism
    [ newPopulation ] = elitism(population, newPopulation, Er);
    
    cgcurve(g) = newPopulation.Chromosomes(1).fitness;
    
    population = newPopulation; % replace the previous population with the newly made
end

   
BestChrom.Gene    = population.Chromosomes(1).Gene;
BestChrom.Fitness = population.Chromosomes(1).fitness;


if visuailzation == 1
    plot( 1 : MaxGen , cgcurve);
    xlabel('Generation');
    ylabel('Fitness of the best elite')
end


end

4.4 initialization.m

function [ population ] = initialization(M, N)

for i = 1 : M
    for j = 1 : N 
        population.Chromosomes(i).Gene(j) = [ round( rand() ) ];
    end
end

4.5 Main.m

clear
clc

%% controling paramters of the GA algortihm
Problem.obj = @Sphere;
Problem.nVar = 20;

M = 20; % number of chromosomes (cadinate solutions)
N = Problem.nVar;  % number of genes (variables)
MaxGen = 100;
Pc = 0.85;
Pm = 0.01;
Er = 0.05;
visualization = 1; % set to 0 if you do not want the convergence curve 

[BestChrom]  = GeneticAlgorithm (M , N, MaxGen , Pc, Pm , Er , Problem.obj , visualization)

disp('The best chromosome found: ')
BestChrom.Gene
disp('The best fitness value: ')
BestChrom.Fitness

4.6 mutation.m

function [child] = mutation(child, Pm)

Gene_no = length(child.Gene);

for k = 1: Gene_no
    R = rand();
    if R < Pm
        child.Gene(k) = ~ child.Gene(k);
    end
end

end

4.7 selection.m

function [parent1, parent2] = selection(population)

M = length(population.Chromosomes(:));

if any([population.Chromosomes(:).fitness] < 0 ) 
    % Fitness scaling in case of negative values scaled(f) = a * f + b
    a = 1;
    b = abs( min(  [population.Chromosomes(:).fitness] )  );
    Scaled_fitness = a *  [population.Chromosomes(:).fitness] + b;
    
    normalized_fitness = [Scaled_fitness] ./ sum([Scaled_fitness]);
else
    normalized_fitness = [population.Chromosomes(:).fitness] ./ sum([population.Chromosomes(:).fitness]);
end



%normalized_fitness = [population.Chromosomes(:).fitness] ./ sum([population.Chromosomes(:).fitness]);

[sorted_fintness_values , sorted_idx] = sort(normalized_fitness , 'descend');

for i = 1 : length(population.Chromosomes)
    temp_population.Chromosomes(i).Gene = population.Chromosomes(sorted_idx(i)).Gene;
    temp_population.Chromosomes(i).fitness = population.Chromosomes(sorted_idx(i)).fitness;
    temp_population.Chromosomes(i).normalized_fitness = normalized_fitness(sorted_idx(i));
end


cumsum = zeros(1 , M);

for i = 1 : M
    for j = i : M
        cumsum(i) = cumsum(i) + temp_population.Chromosomes(j).normalized_fitness;
    end
end


R = rand(); % in [0,1]
parent1_idx = M;
for i = 1: length(cumsum)
    if R > cumsum(i)
        parent1_idx = i - 1;
        break;
    end
end

parent2_idx = parent1_idx;
while_loop_stop = 0; % to break the while loop in rare cases where we keep getting the same index
while parent2_idx == parent1_idx
    while_loop_stop = while_loop_stop + 1;
    R = rand(); % in [0,1]
    if while_loop_stop > 20
        break;
    end
    for i = 1: length(cumsum)
        if R > cumsum(i)
            parent2_idx = i - 1;
            break;
        end
    end
end

parent1 = temp_population.Chromosomes(parent1_idx);
parent2 = temp_population.Chromosomes(parent2_idx);

end

4.8 Sphere.m

function  [fitness_value] = Sphere( X )
  
   
   fitness_value = sum(X.^2);

end

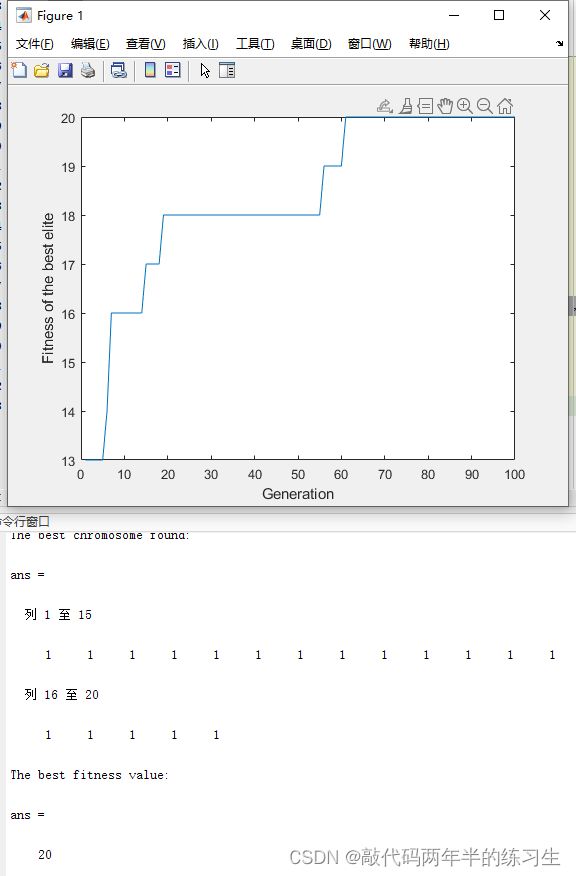
5.运行结果

6.参考文献

[1]Hayes-Roth F. Review of “Adaptation in Natural and Artificial Systems by John H. Holland”, The U. of Michigan Press, 1975[J]. ACM SIGART Bulletin,1975,53(53).