狄克斯特拉算法-解决有向有权图的最短路径问题【完结篇】（算法快速入门-基于《算法图解》的算法入门教程(4)）

---

一、前言

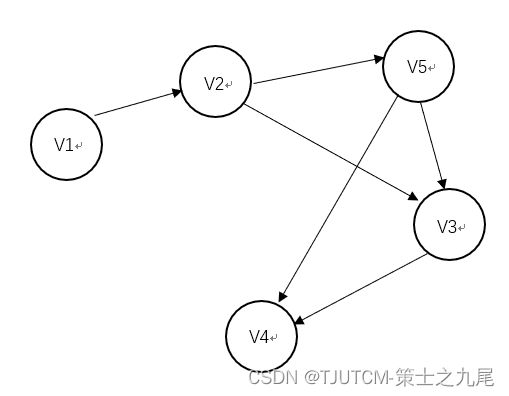
  在前一节，我们找到了从v1到v4的最短路径。显然v1→v2→v5→v4和v1→v2→v5→v4是我们想要的最短路径——它们都只有4段。但如果我们给这些路径加上距离(权值)，它们不见得依然是最短路径。

  在前一章我们使用了广度优先搜索(即对应于第一张有向无权图)，它找出的是段数最少的路径。如果我们要找出最快的路径，该怎么办呢？为此，可使用另一种算法——狄克斯特拉算法（Dijkstra’s algorithm）。

---

二、使用狄克斯特拉算法

  下面我们来看看如何对之前的有向有权图使用这种算法。

  图中各边上的每个数字表示的都是时间(这里把单位都用分钟来表示)，表示从起始节点到终止结点的距离(这里定义为权值)。为找出从起点v1到终点v4耗时最短的路径，我们将使用狄克斯特拉算法。
  如果我们使用广度优先搜索，将得到这条段数最少的路径：v1→v2→v5→v3→v4。这条路径耗时7分钟。下面我们来检查一下，看看能否找到耗时更短的路径。

狄克斯特拉算法包含4个步骤：

(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。

(2) 更新该节点的邻居的开销，我们将在稍后解释其含义。

(3) 重复这个过程，直到对图中的每个节点我们都做过了以上的操作。

(4) 大功告成！计算最终路径

---

三、具体拆分步骤：

第一个小步骤:找出最便宜的节点

  ①v1想要到达v4结点必须经过v2，所以我们先选择v2结点。
  ②到达v2结点后，我们可以选择v3或者v5结点。前往v3需要3分钟，而前往v5只需要1分钟。至于前往其他节点，我们现在还不知道需要多长时间。
  由于我们还不知道前往终点需要多长时间，因此我们假设为无穷大。
  而结点v5是最近的——我们只需要1分钟就能达到。

结点	耗时
v3	6
v5	4
v4(终点)	∞

第二个小步骤:计算经v5结点前往其各个邻居所需的时间

结点	耗时
v3	5
v5	4
v4(终点)	8

  我们找到了一条前往结点v3的更短路径！
  直接由结点v2前往结点v3需要6分钟，而我们由结点v2经过v5再前往v3只需要5分钟。
  对于结点v2的邻居，如果找到前往下一个结点的更短路径，我们就更新其开销。在这一步，我们实现了：
    ①前往节点A的更短路径（时间从6分钟缩短到5分钟）；
    ②前往终点的更短路径（时间从无穷大缩短到8分钟）。

第三个小步骤：根据已到达结点，算出到达终点的最短路径

  我们现在已到达的结点为：结点v1、v2、v5、v3。现在，让我们更新到达终点v4的最短路径吧！

结点	耗时
v3	5
v5	4
v4(终点)	7

  这里解释一下：因为我们前一步更新了到达结点v3的最短距离为5，在这一步我们通过v3到达终点v4，发现耗时(距离)只有7！所以我们更新结点、耗时表，将到达v4结点的耗时改为7。

小结

  这里我们对狄克斯特拉算法做一个小结，狄克斯特拉算法包含4个步骤：
    (1)找出最便宜的节点，即可在最短时间内前往的节点。
    (2)对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。
    (3)重复这个过程，直到对图中的每个节点都这样做了。
    (4)计算最终路径。
  只要我们根据上述步骤，就能使用狄克斯特拉算法有效解决有向有权图的最短路径问题

---

四、术语详解

  狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重（weight）。
  带权重的图称为加权图（weighted graph），不带权重的图称为非加权图（unweighted graph）。
  要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。
  图还可能有环，这意味着我们可从一个节点出发，走一圈后又回到这个节点。我们只要每绕环一次，总权重都会增加。因此，绕环的路径不可能是最短的路径。

---

五、实现步骤

  下面我们来看看如何使用代码来实现狄克斯特拉算法，这里以下面的图为例。

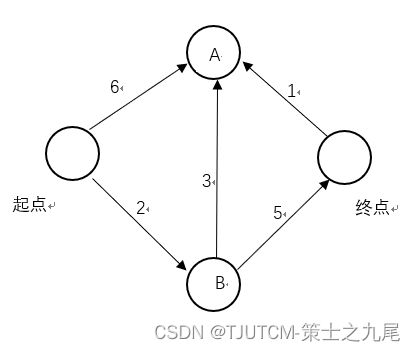
  要编写解决这个问题的代码，我们需要两个散列表，它们分别为costs表和parents表：

结点	距离
A	6
B	2
终点	∞

结点	邻居
A	起点
B	起点
终点	-

  随着算法的进行，你将不断更新散列表costs和parents。
  之前，我们像下面这样将节点的所有邻居都存储在散列表中：

graph["v1"] = ["v2", "v3", "v4"] 

  但这里需要同时存储邻居和前往邻居的开销。例如，起点有两个邻居——A和B。
  我们可以再用一个散列表实现这个要求。

graph["start"] = {} 
graph["start"]["a"] = 6 
graph["start"]["b"] = 2 
#这个散列表又包含散列表

  因此graph[“start”]是一个散列表。要获取起点的所有邻居，我们可像下面这样做：

>>> print graph["start"].keys() 
["a", "b"] 

  下面来添加其他节点及其邻居

graph["a"] = {} 
graph["a"]["fin"] = 1 
graph["b"] = {} 
graph["b"]["a"] = 3 
graph["b"]["fin"] = 5 
graph["fin"] = {} 		#终点没有任何邻居

  接下来，需要用一个散列表来存储每个节点的开销。
  节点的开销指的是从起点出发前往该节点需要多长时间。我们知道，从起点到节点B需要2分钟，从起点到节点A需要6分钟（但你可能会找到所需时间更短的路径）。
  可是，我们一开始是不知道到终点需要多长时间的。对于还不知道的开销，我们可以将其设置为无穷大，在Python中我们可以这样实现：

infinity = float("inf")

  创建开销表的代码如下：

infinity = float("inf") 
costs = {} 
costs["a"] = 6 
costs["b"] = 2 
costs["fin"] = infinity

  我们还需要一个存储父节点的散列表，创建这个散列表的代码如下：

parents = {} 
parents["a"] = "start" 
parents["b"] = "start" 
parents["fin"] = None 

  最后，我们还需要一个数组，用于记录处理过的节点，因为对于同一个节点，不用处理多次。

---

六、最终实现

node = find_lowest_cost_node(costs)	#在未处理的节点中找出开销最小的节点
while node is not None:				#这个while循环在所有节点都被处理过后结束
	cost = costs[node] 
	neighbors = graph[node] 
	for n in neighbors.keys(): 		#遍历当前节点的所有邻居
		new_cost = cost + neighbors[n] 
		if costs[n] > new_cost:		
		#如果经当前节点前往该邻居更近，就更新该邻居的开销
		#同时将该邻居的父节点设置为当前节点
			costs[n] = new_cost
			parents[n] = node	#将当前节点标记为处理过
	processed.append(node)		#将当前节点标记为处理过
	node = find_lowest_cost_node(costs)	#找出接下来要处理的节点，并循环

def find_lowest_cost_node(costs): 
	lowest_cost = float("inf") 
	lowest_cost_node = None 
	for node in costs:			#遍历所有的节点
		cost = costs[node] 
		if cost < lowest_cost and node not in processed:
		#如果当前节点的开销更低且未处理过
			lowest_cost = cost	#就将其视为开销最低的节点
			lowest_cost_node = node 
		return lowest_cost_node

---

  《算法图解》中还提到了关于贪心算法、动态规划、K最邻近算法等相关内容，虽然保留了本书一贯的讲解生动的特点，但我并不认为这能很好地帮助我们形成相应的知识框架。因此，本系列就到此为止了！
  接下来我将着力于代码而非简单的算法入门思想，使用**《计算机算法设计与分析》**（第五版）（王晓东编著）这本书，并对其中的难题更新博客，感谢您的阅读，不久见！