机器学习(三):实操线性回归案例_实现设备产能预测
全文共20000余字,预计阅读时间约1~1.5小时 | 满满干货,建议收藏!
1. 介绍
1.1 背景介绍
在日常生活中,有许多的问题需要我们通过数据来进行预测。例如,我们可能需要预测一个设备的运行效率,这将依赖于一系列的变量,如设备的特性,使用环境,以及其它可能的因素。为了解决这样的问题,我们将使用线性回归和多元线性回归的方法,通过建立模型来进行预测。
为此,我获取了一份适合于此项目的数据集,它包含了一年的时间内,一种设备的各种属性及其在特定环境下的表现。然而,为了保护数据的隐私,我要先对数据进行了脱敏处理。并且,后续提供的数据集,也将是脱敏后的数据集。但是请大家放心,脱敏后的数据集将保留原数据的结构和特性,但不再包含任何可以识别个体的信息,从而确保了数据的安全使用。
这份数据集并非专为此项目设计,而是我根据项目需求从公开渠道获取并进行处理的。因此,这份数据集的使用将为我们提供了一个很好的实践机会,让我们能够在一个实际的场景中应用线性回归和多元线性回归的方法。
1.2 项目目标
我们的项目有两个主要的目标,分别是数据脱敏和模型建立
-
数据脱敏: 我们首先需要对数据进行脱敏处理,以保护相关个体的隐私。在这个过程中,我们将使用Python的Pandas库,它提供了丰富的数据处理功能,可以帮助我们轻松完成数据脱敏。
-
建立预测模型: 脱敏处理后,我们将利用这份数据集,通过线性回归和多元线性回归,建立一个预测模型。这个模型的目标是预测设备在给定的条件下的表现。我们希望通过这个模型,能够对设备的表现做出准确的预测,从而为决策提供支持
2. 数据集描述
链接: 数据集及代码下载点这里
提取码:v8gy
2.1 数据集概览
在这个部分,我们将会使用一份已经经过脱敏处理的数据集。这意味着我们不会直接使用原始数据集中的字段。相反,我们将会使用一组经过修改和脱敏处理的字段,这些字段被设计得既可以保护原始数据的隐私,又能保留原始数据中的关键信息,以便我们可以进行有效的数据分析和建模。
2.2 数据脱敏
数据脱敏是一种保护隐私的技术,它通过修改数据以隐藏个体的敏感信息,从而防止这些信息被非法获取或滥用。脱敏处理后的数据仍然保留了原始数据的一些关键特性,例如数据的分布、关联和结构,这使得它们仍然可以用于各种数据分析和数据挖掘的任务。
2.3 实操数据脱敏
为了让大家更直观的理解脱敏过程中都做了什么操作,下面的代码针对每一个字段我都单独进行的处理,同时也提供了优化的代码,大家可以下载上面提供的代码和数据集的链接查看。先看下代码:
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
# 读取数据
df = pd.read_csv('realdata.csv')
# 删除包含任何空值的行
df = df.dropna(how='any')
# 脱敏户籍ID
df['Household_ID'] = ['ID' + str(i) for i in range(len(df))]
# 脱敏城市
le_city = LabelEncoder()
df['City'] = le_city.fit_transform(df['City'])
# 添加随机噪声到纬度
df['Latitude'] = df['Latitude'] + np.random.normal(0, 0.01, len(df))
# 脱敏房屋类型
le_house_type = LabelEncoder()
df['House_Type'] = le_house_type.fit_transform(df['House_Type'])
# 脱敏屋顶类型
le_roof_type = LabelEncoder()
df['Roof_Type'] = le_roof_type.fit_transform(df['Roof_Type'])
# 扰动屋顶坡度
df['Roof_Pitch'] = df['Roof_Pitch'] + np.random.normal(0, 0.01, len(df))
# 扰动屋顶方位
df['Roof_Azimuth'] = df['Roof_Azimuth'] + np.random.normal(0, 0.01, len(df))
# 扰动楼层数
fl_type = LabelEncoder()
df['Floors'] = fl_type.fit_transform(df['Floors'])
# 脱敏融资情况
le_financed = LabelEncoder()
df['Financed'] = le_financed.fit_transform(df['Financed'])
# 扰动年份
df['Year'] = df['Year'] + np.random.randint(-1, 2, len(df))
# 扰动面板容量
df['Panel_Capacity'] = df['Panel_Capacity'] + np.random.normal(0, 0.01, len(df))
# 扰动遮挡情况
sd_financed = LabelEncoder()
df['Shading'] = sd_financed.fit_transform(df['Shading'])
# 旧的字段名称
old_names = ['Household_ID', 'City', 'Latitude', 'House_Type', 'Roof_Type', 'Roof_Pitch', 'Roof_Azimuth', 'Floors', 'Financed', 'Year', 'Panel_Capacity', 'Shading', 'Generation']
# 新的字段名称
new_names = ['Identifier', 'Area', 'Position', 'Type', 'Device_Kind', 'Angle_of_Installation', 'Device_Orientation', 'Levels', 'Financing_Status', 'Year', 'Device_Capability', 'Degree_of_Shading', 'Production']
# 使用rename函数,将旧的字段名称替换为新的字段名称
df.rename(columns=dict(zip(old_names, new_names)), inplace=True)
# 保存适配后的数据到本地文件
df.to_csv('data_anonymized.csv', index=False)
总结一下上述流程:脱敏过程删除了所有包含空值的行,对所有的户籍ID都被赋予了一个新的唯一标识符,使用标签编码器将所有的分类变量(如城市、房屋类型、屋顶类型等)转化为数值,从而进行脱敏。然后在所有连续变量(如纬度、屋顶坡度等)上添加了随机噪声,以此达到脱敏的目的。同时,对于特殊的年份数据,我们添加了随机偏移。最后,我们将所有的字段名称替换为新的字段名称,具体描述看下一节。
2.4 数据集变量详解
| 字段名称 | 描述 |
|---|---|
| 标识码(Identifier) | 这是每个实例的唯一标识符,已经进行了脱敏处理。 |
| 区域(Area) | 表示实例的一般地理区域,已经进行了脱敏处理。 |
| 位置(Position) | 表示实例的一般地理位置,已经进行了脱敏处理。 |
| 类型(Type) | 表示实例的主要类型。 |
| 设备种类(Device_Kind) | 表示装置的种类。 |
| 安装角度(Angle_of_Installation) | 表示装置的安装角度。 |
| 设备朝向(Device_Orientation) | 表示装置面向的角度。 |
| 层数(Levels) | 表示实例的层数量。 |
| 融资状态(Financing_Status) | 表示装置是否正在通过安装商或供应商进行融资安排。 |
| 年份(Year) | 装置的安装年份。 |
| 设备能力(Device_Capability) | 根据制造商的数据表,装置的总能力(单位)。 |
| 遮挡程度(Degree_of_Shading) | 安装商预计装置将受到的来自附近环境(如树木或人造结构)的遮挡量。 |
| 产能(Production) | 采样期间(从2022年1月1日到2022年12月31日)的总产能(单位)。 |
在后面的建模过程中,我们将使用经过脱敏和预处理的data_anonymized.csv数据集。因为这个数据集已经过适当的清洗和处理,在进行进一步的数据预处理后,就可用于训练线性回归模型。在训练过程中,可以通过优化模型参数来最大化模型的预测准确性,从而达到我们的预测目标。
3. 数据预处理
通过查看2.3节的过程,可以认为在一定程度上代表了数据的预处理,因为它进行了数据清洗(删除包含空值的行)、数据脱敏(对个人信息和敏感信息进行了处理)以及数据整理(对字段名称进行了改变)。这些步骤都是在进行任何模型训练之前需要进行的重要步骤。特别是在进行线性回归建模时,这些步骤更是必不可少,因为线性回归模型要求输入数据没有空值,所有的分类变量需要被转化为数值,而且必须确保输入数据的安全性和隐私性。但是在对data_anonymized.csv数据集,还要进行更进一步的数据预处理
3.1 数据探索
3.1.1 数据探索的意义
数据探索(也称为探索性数据分析,EDA)是数据分析的第一步,它可以帮助我们理解数据集的主要特征、结构、模式以及异常值等。通过数据探索,我们可以了解到数据的分布、相关性以及可能存在的异常值。这对于后续的数据预处理和建模非常重要,因为我们可以根据数据探索的结果来决定如何最好地清理和转换数据以适应模型。所以第一步我们要进行对未知数据集的探索工作
3.1.2 数据探索的重要性
数据探索的重要性主要体现在以下几个方面:
- 帮助我们检查数据的质量,例如是否存在缺失值或异常值。
- 帮助我们理解数据的分布。这对于选择合适的模型或者调整模型参数非常重要。
- 帮助我们发现数据的模式和趋势,这对于理解数据非常有帮助。
- 通过数据探索,我们可以发现变量之间的关系,这对于建模前的特征工程和模型选择非常重要
3.1.3 常用的数据探索方式
数据的探索方式有很多,常用的数据探索方式如:
-
描述性统计分析:这包括计算各个特征的均值、中位数、模式、标准差、四分位数等。
-
数据可视化:使用各种图表(如直方图、箱线图、散点图等)来展示数据的分布和关系。
-
相关性分析:通过计算特征之间的相关性,我们可以了解哪些特征可能对我们的预测目标有影响。
-
异常值检测:识别和处理异常值对于提高模型的性能非常重要。
3.1.4 变量相关性基础理论
变量彼此之间的相关性,是我们探究数据规律的重要手段。尽管相关性理论发源于经典统计理论体系,但对于机器学习,相关性也是数据探索、特征工程环节的重要理论。机器学习的“学习”目标,其实就是数据集中隐藏的数字规律,而又由于这些规律背后代表的是某些事物的真实属性或者运行状态,因此这些规律是具备指导生产生活事件意义的有价值的规律,这也是机器学习算法价值的根本。
3.1.5 相关系数的概念及计算公式
对于不同数据集来说,是否具备规律、以及规律隐藏的深浅都不一样。不同的模型挖掘规律、以及规律挖掘的能力也都各不相同。而对于线性回归来说,捕捉的实际上是数据集的线性相关的规律。所谓线性相关,简单来说就是数据的同步变化特性。
以下是一个假设性的数据集,描述了汽车的“重量”与“燃油效率”之间的关系。在实际情况中,汽车的重量越大,燃油效率往往越低,这是因为更重的车需要更多的能量来推动,从而消耗更多的燃料。
| Weight (in tons) | Fuel Efficiency (miles per gallon) |
|---|---|
| 1.5 | 30 |
| 2 | 25 |
| 2.5 | 22 |
| 3 | 20 |
| 3.5 | 18 |
| 4 | 16 |
| 4.5 | 15 |
| 5 | 13 |
在这个例子中,“Weight”和“Fuel Efficiency”可能存在线性关系,即当汽车的重量增加时,其燃油效率可能会降低。我们可以通过绘制散点图或计算相关系数来进一步验证这两个变量之间的关系。如果他们之间存在线性关系,那么我们可以使用线性回归模型来预测给定汽车重量的燃油效率。
这种相关性可以用一个计算公式算得,也就是相关性系数计算公式:
C o r r e l a t i o n = C o v ( X , Y ) V a r ( X ) ∗ V a r ( Y ) Correlation = \frac{Cov(X, Y)}{\sqrt {Var(X) * Var(Y)}} Correlation=Var(X)∗Var(Y)Cov(X,Y)
其中, X X X和 Y Y Y是两个随机变量(对应数据集也就代表两个字段), V a r ( X ) 、 V a r ( Y ) Var(X)、Var(Y) Var(X)、Var(Y)为 X 、 Y X、Y X、Y的方差, C o v ( X , Y ) Cov(X,Y) Cov(X,Y)为 X X X和 Y Y Y这两个变量的协方差,具体计算公式为:
C o v ( X , Y ) = E ( X − E ( X ) ) E ( Y − E ( Y ) ) = E ( X Y ) − E ( X ) E ( Y ) \begin{align} Cov(X, Y) &= E(X-E(X))E(Y-E(Y)) \\ &=E(XY)-E(X)E(Y) \end{align} Cov(X,Y)=E(X−E(X))E(Y−E(Y))=E(XY)−E(X)E(Y)
其中 E ( X ) 、 E ( Y ) E(X)、E(Y) E(X)、E(Y)为 X 、 Y X、Y X、Y期望计算结果。
这种相关系数计算也被称为皮尔逊相关系数,最早由统计学家卡尔·皮尔逊提出,是目前最为通用的相关系数计算方法。
3.1.6 实操:计算相关性系数
在NumPy中也提供了相关系数计算函数corrcoef可用于快速计算两个数组之间的相关系数,numpy.corrcoef()函数返回的是一个2x2的相关性矩阵,其中对角线元素是自身的相关性(总是1),非对角线元素是两个变量之间的相关性。
注意:这里的相关性是皮尔逊相关性,测量的是两个变量之间的线性关系。相关性值的范围是-1到1,-1表示完全的负相关,1表示完全的正相关,0表示无相关性。
import numpy as np
# 首先,我们需要将表格数据转化为NumPy数组,然后使用numpy.corrcoef()函数进行相关性计算
# 表格数据
weight = np.array([1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5])
fuel_efficiency = np.array([30, 25, 22, 20, 18, 16, 15, 13])
# 计算相关性矩阵
correlation_matrix = np.corrcoef(weight, fuel_efficiency)
print(correlation_matrix)
输出如下:
[[ 1. -0.9767344]
[-0.9767344 1. ]]
结果解读:
这是一个2x2的相关性矩阵。在这个矩阵中:
- 第一行第一列的数值1代表的是weight(重量)与自身的相关性,这个值永远都是1,因为任何变量与自身的相关性总是最大的。
- 第二行第二列的数值1同样代表的是fuel_efficiency(燃油效率)与自身的相关性,同样这个值也是1。
- 第一行第二列的数值-0.9767344代表的是weight与fuel_efficiency之间的相关性。这个数值非常接近-1,表示weight与fuel_efficiency之间存在非常强烈的负相关性。也就是说,weight增加,fuel_efficiency就会减少。
- 第二行第一列的数值-0.9767344同样代表的是fuel_efficiency与weight之间的相关性,它与第一行第二列的数值完全相同,因为相关性是无方向的,A与B的相关性等同于B与A的相关性。
因此,这个相关性矩阵告诉我们,重量(weight)与燃油效率(fuel_efficiency)之间存在非常强的负相关关系。也就是说,汽车的重量越大,其燃油效率通常就越低。
当绝对值介于0和1之间时候,相关性强弱可以表示如下:
| |Cor| | 相关性 |
|---|---|
| 0~0.09 | 没有相关性 |
| 0.1~0.3 | 弱相关 |
| 0.3~0.5 | 中等相关 |
| 0.5~1.0 | 强相关 |
在上一篇的线性回归理论文章中我们说到过,线性回归就是在二维平面中通过构建一条直线来试图捕捉平面当中的点,线性相关性越弱、线性模型越难捕捉到这些所有点,模型效果就越差。换而言之,就是数据集之间线性相关性越明显,数据规律越明显,模型越容易捕捉到这些规律。
import matplotlib.pyplot as plt
import numpy as np
# 创建数据
weight = np.array([1.5, 2.3, 3.7, 2.2, 2.9, 4.1, 3.8, 2.6, 3.4, 4.6])
fuel_efficiency = np.array([38, 37, 32, 36, 34, 31, 32, 35, 33, 30])
# 创建散点图
plt.figure(figsize=(8, 6))
plt.scatter(weight, fuel_efficiency)
plt.title('Scatter plot of weight vs fuel efficiency')
plt.xlabel('Weight')
plt.ylabel('Fuel Efficiency')
plt.grid(True)
# 创建线性回归线在这里插入图片描述
m, b = np.polyfit(weight, fuel_efficiency, 1)
plt.plot(weight, m*weight + b, color='red')
plt.show()
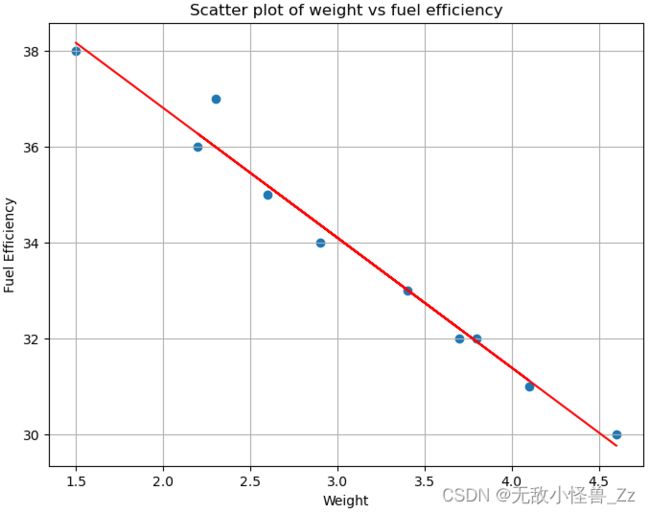
上述代码生成一个散点图,图中的每个点代表一个汽车重量和其对应的燃油效率。红色的线是根据这些点拟合出来的线性回归线,表示汽车重量和燃油效率之间的相关性。
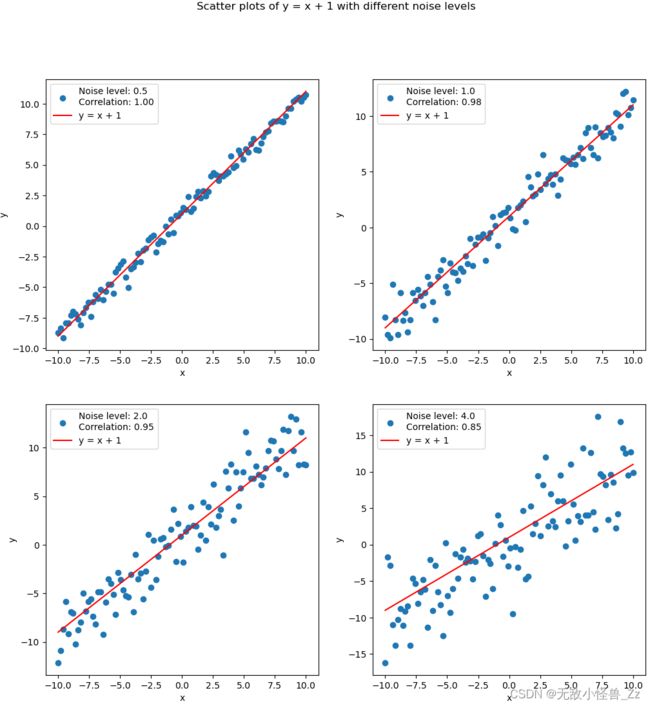
下面我们定义一个x的范围,然后定义四个不同的噪声级别。对于每个噪声级别,我们生成相应的噪声,并将其添加到理论上的y = x + 1中,从而得到实际的y值。然后,我们计算x和y的相关性,并在子图中绘制散点图和理论线
import numpy as np
import matplotlib.pyplot as plt
# 创建x
x = np.linspace(-10, 10, 100)
# 创建四个扰动项
noise_levels = [0.5, 1.0, 2.0, 4.0]
# 创建四个子图
fig, axs = plt.subplots(2, 2, figsize=(12, 12))
# 对于每个扰动项
for i, noise_level in enumerate(noise_levels):
# 创建扰动
noise = np.random.normal(0, noise_level, len(x))
# 创建y
y = x + 1 + noise
# 计算相关性
correlation = np.corrcoef(x, y)[0, 1]
# 绘制散点图
axs[i//2, i%2].scatter(x, y, label=f'Noise level: {noise_level}\nCorrelation: {correlation:.2f}')
axs[i//2, i%2].plot(x, x + 1, 'r', label='y = x + 1') # 理论线
# 设置图例和标签
axs[i//2, i%2].legend()
axs[i//2, i%2].set_xlabel('x')
axs[i//2, i%2].set_ylabel('y')
# 设置标题
plt.suptitle('Scatter plots of y = x + 1 with different noise levels')
plt.show()
能够明显看出,伴随噪声级别的取值越来越大,数据相关性越来越弱。
所以我们可以得出结论:
在构建线性模型之前先探查数据本身的线性相关性,如果自变量和因变量存在很好的相关性,那就一定可以顺利的构建线性回归模型对数据进行拟合。而如果线性相关性不强,则说明当前数据并不适合构建线性回归模型,或者在构建模型之前我们需要对数据进行一些“不影响真实规律”的转化,令其表现出线性的分布趋势。
上述几组不同的数据,实际上就代表着对线性回归模型建模难度各不相同的几组数据,噪声级别越大对线性回归模型来说建模就更加困难。
3.2 数据清洗
数据清洗一般包括以下步骤:
-
检查缺失值并决定如何处理它们。
-
通过各种统计方法完成,如标准差方法、箱线图(IQR)方法、Z-score方法等检测异常值。也可以通过数据可视化来观察,例如使用散点图、箱线图等。发现异常值后,有多种处理方法,包括删除包含异常值的观察、将异常值替换为其他值(如平均值、中位数等)、或者将异常值当作缺失值处理等。具体处理方式需要根据异常值的性质、数据集的大小以及具体的业务场景来决定。
-
对于分类变量,可能需要进行一些编码,比如独热编码或者标签编码,具体取决于你选择的模型和这些变量的性质。
-
对于连续变量,可能需要进行一些归一化或者标准化的操作,以避免由于尺度不同而导致的问题。
-
根据你选择的模型,可能需要创建一些额外的交互特征。
异常值处理是数据预处理的重要部分。异常值可能会对模型的学习产生不良影响,特别是在一些模型中,例如线性回归,异常值会对模型的性能产生较大影响,预处理完成后,就可以用预处理后的数据来训练线性回归模型,并对"Production"进行预测。
我们可以看到,在数据脱敏的过程中,我们已经完成了处理缺失值及分类变量的编码,那么我们继续后续的数据清洗过程。
from scipy import stats
from sklearn.preprocessing import StandardScaler
# 将Z分数大于3或小于-3的点视为离群值
z_scores = np.abs(stats.zscore(df_anonymized._get_numeric_data()))
df_anonymized = df_anonymized[(z_scores < 3).all(axis=1)]
# 将连续变量进行标准化
scaler = StandardScaler()
continuous_columns = ['Position', 'Angle_of_Installation', 'Device_Orientation', 'Year', 'Device_Capability']
df_anonymized[continuous_columns] = scaler.fit_transform(df_anonymized[continuous_columns])
在上述代码中,我们首先为数据框中的每个值计算Z分数,该分数衡量了一个点离平均值有多少个标准差。一种常见的选择是将Z分数大于3或小于-3的点视为离群值(即,偏离均值超过3个标准差)。这就是 (z_scores < 3).all(axis=1) 所做的:它为所有Z分数低于3的行创建了一个布尔掩码。
在过滤掉离群值后,我们使用StandardScaler标准化数据框中的连续变量,这将使特征标准化,使它们具有0的均值和1的标准差。连续变量的列是由数据的性质和上下文决定的。
3.3 数据探索性分析
我们可以利用上一节的讲到的相关性系数,来计算这个数据集的相关性
import seaborn as sns
import matplotlib.pyplot as plt
# 计算相关性
corr_matrix = df_anonymized.corr()
# 画出相关性矩阵的热力图
plt.figure(figsize=(12, 8))
sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap='coolwarm', cbar=True, square=True)
plt.title('Correlation Matrix')
plt.show()
在这段代码中,我们首先计算了数据框中所有特征之间的相关性,然后使用seaborn库的heatmap函数来绘制相关性矩阵的热力图。热力图中的每个单元格的颜色表示相应特征之间的相关性,颜色越深表示相关性越强。"annot=True"参数表示在单元格中显示相关性数值,"fmt=‘.2f’"参数表示保留两位小数,"cmap=‘coolwarm’"参数表示使用coolwarm颜色映射,颜色从蓝色(负相关)到红色(正相关)变化,"cbar=True"参数表示显示颜色条。
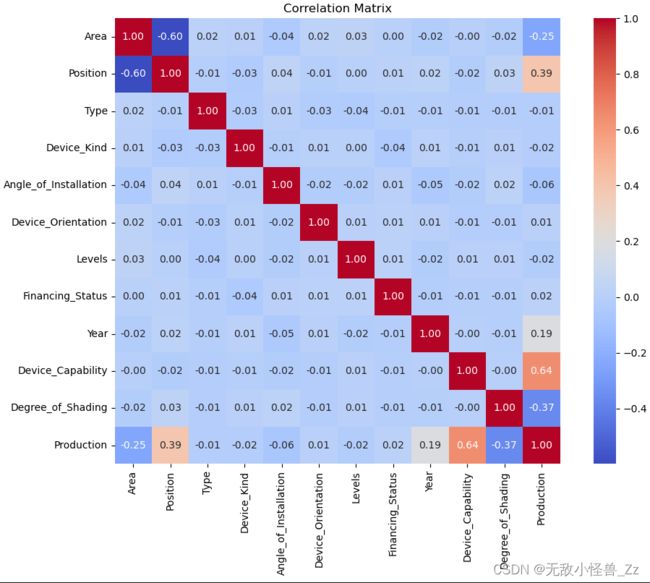
最后,我们使用matplotlib库来显示热力图,如下:
这是一个相关性矩阵,它显示了数据集中所有变量之间的相关性。在矩阵中,每个单元格的值都代表了行标签和列标签所代表的两个变量之间的相关性。相关性的值范围是从-1到1,其中:
-
值接近1:表示两个变量之间存在强烈的正相关关系。这意味着当一个变量的值增加时,另一个变量的值也会增加。
-
值接近-1:表示两个变量之间存在强烈的负相关关系。这意味着当一个变量的值增加时,另一个变量的值会减少。
-
值接近0:表示两个变量之间没有或只有很弱的相关性。
-
根据这个相关性矩阵,我们可以解读到以下信息:
-
“Production”(产量)和"Device_Capability"(设备能力)之间有较强的正相关(0.644044),这意味着设备的能力越高,产量也越高。
-
“Production”(产量)和"Degree_of_Shading"(遮挡程度)之间有较强的负相关(-0.365176),这可能意味着遮挡程度越高,产量越低。
-
“Production”(产量)和"Position"(位置)之间有一定的正相关(0.388358),这可能意味着某些位置的设备产量更高。
-
“Production”(产量)和"Area"(区域)之间有一定的负相关(-0.246654),这可能意味着某些区域的设备产量较低。
-
“Production”(产量)和"Year"(年份)之间有一定的正相关(0.187853),这可能意味着随着年份的增加,产量也在增加。
3.4 多重共线性
如果两个或多个自变量之间存在高度相关性,可能会导致多重共线性问题。这可能会使得模型的参数估计变得不稳定,降低模型的解释能力。在你的数据中,如果存在多重共线性,你可能需要移除一些相关性较高的特征,或者通过一些方法(如主成分分析)来降低特征之间的相关性。
使用 statsmodels 库中的 variance_inflation_factor 函数来计算多重共线性
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 在计算VIF之前,你需要确保你的数据集中只包含数值类型的特征。
df_numeric_features = df_features.select_dtypes(include=[np.number])
# 向数据框添加一个常量。这是VIF计算所必需的
df_numeric_features = df_numeric_features.assign(const=1)
# 计算每个特征的VIF
vif = pd.DataFrame()
vif["Features"] = df_numeric_features.columns
vif["VIF"] = [variance_inflation_factor(df_numeric_features.values, i) for i in range(df_numeric_features.shape[1])]
print(vif)
这段代码将计算出数据集中每个特征的方差膨胀因子(VIF)。VIF 是一个衡量多重共线性程度的指标,即一个变量被其他变量预测的程度。VIF 值大于 5 或 10 通常被认为存在较高的多重共线性。这种高度的多重共线性可能会影响你的线性回归模型的性能。如果你发现某个特征的 VIF 值较高,你可能需要考虑从模型中移除这个特征,或者采用降维技术。
上段代码输出的结果如下:
Features VIF
0 Area 1.564848
1 Position 1.565347
2 Type 1.003780
3 Device_Kind 1.004002
4 Angle_of_Installation 1.005934
5 Device_Orientation 1.002471
6 Levels 1.004030
7 Financing_Status 1.002895
8 Year 1.004033
9 Device_Capability 1.001885
10 Degree_of_Shading 1.002130
11 const 24.456424
在结果中,所有变量的VIF都小于5,这意味着没有明显的多重共线性问题。"const"的VIF值较高,这是因为"const"是我们添加的常数项,用于计算VIF,它的VIF值并不表示多重共线性。
所以,根据这个结果,我们不需要删除任何列。但是这一过程,我们是很有必要进行探索的
3.5 特征选择
不是所有的特征都对预测目标变量有用。在数据中,一些特征与目标变量的相关性较低,可能不会对模型预测产生显著影响。因此,你可能需要进行特征选择,只保留那些与目标变量相关性较高的特征。
# 定义相关性阈值
correlation_threshold = 0.2
# 计算每个特征与目标变量之间的相关性
correlations = df_anonymized.corr()['Production']
# 找出那些与目标变量相关性大于阈值的特征
features_above_threshold = correlations[correlations.abs() > correlation_threshold].index
print("Features above threshold:", features_above_threshold)
# 找出那些与目标变量相关性小于阈值的特征
features_below_threshold = correlations[correlations.abs() <= correlation_threshold].index
print("Features below threshold:", features_below_threshold)
# 只保留那些与目标变量相关性大于阈值的特征
features_to_keep = correlations[correlations.abs() > correlation_threshold].index
df_anonymized = df_anonymized[features_to_keep]
这里的特征选择方法比较简单,只考虑了单变量的相关性,没有考虑多变量之间可能存在的交互效应。更复杂的特征选择方法,如递归特征消除(Recursive Feature Elimination, RFE),则可以考虑到多变量的交互效应。然而,这些方法通常需要更多的计算资源。
另外,特征选择是一个需要根据具体情况进行的过程,可能需要多次尝试和调整。在某些情况下,即使某个特征与目标变量的相关性不高,它也可能在模型中起到重要作用。所以,特征选择需要根据实际情况和专业知识进行。
4. 线性回归
接下来,我们尝试进行线性回归模型的建模实验。建模过程将遵照机器学习的一般建模流程,如果不清楚的看这里:机器学习(一):理解机器学习相关概念,并且借助NumPy所提供的相关工具来进行实现。通过本次实验,我们将进一步深化对机器学习建模流程的理解,并且也将进一步熟悉对编程基础工具的掌握。
4.1 数据准备
我们经过上面的数据脱敏、数据预处理、数据清洗、相关性分析、特征选择等,得到了处理好的数据集,首先要进行划分数据集:将数据集划分为训练集和测试集。训练集用于训练模型,测试集用于评估模型的性能。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 1. 划分数据集
X = df_anonymized.drop('Production', axis=1) # 输入特征
y = df_anonymized['Production'] # 目标变量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
4.2 模型选择
在这个任务中,我们要实例化线性模型,对上述回归类问题数据进行建模。此处我们选取带有截距项的多元线性回归方程进行建模,基本模型为:
f ( x ) = w 1 x 1 + w 2 x 2 + b f(x) = w_1x_1+w_2x_2+b f(x)=w1x1+w2x2+b
可以直接通过sklearn库建立
# 2. 建立模型
model = LinearRegression()
4.3 构造损失函数
构造损失函数,在这个步骤中,会使用测试集来评估模型的性能。可以使用一种或多种评估指标,比如均方误差(MSE)、均方根误差(RMSE)或R^2分数。比如SSE的计算公式:不清楚的看这里专栏开篇:揭开机器学习神秘面纱
S S E = ∣ ∣ y − X w ^ ∣ ∣ 2 2 = ( y − y ^ ) T ( y − y ^ ) SSE= ||y - X\hat w||_2^2 = (y - \hat y)^T(y - \hat y) SSE=∣∣y−Xw^∣∣22=(y−y^)T(y−y^)
4.4 利用最小二乘法求解损失函数
sklearn.linear_model.LinearRegression 默认使用的是普通最小二乘法(Ordinary Least Squares,OLS)进行求解。最小二乘法是一种常用的参数估计方法,目标是最小化预测值与实际值之间的平方差。
请注意,虽然最小二乘法是一种常用且有效的方法,但当特征矩阵X不是满秩(即某些特征之间线性相关)或者数据中存在较大的噪声时,最小二乘法可能会得到不准确的结果。在这种情况下,可能需要使用其他的回归方法,如岭回归(Ridge Regression)或Lasso回归等。
# 3. 训练模型
model.fit(X_train, y_train)
# 4. 评估模型
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
# 计算 SSE
sse = np.sum((y_test - y_pred) ** 2)
# 计算 RMSE
rmse = np.sqrt(mse)
print(f"MSE: {mse}")
print(f"RMSE: {rmse}")
print(f"MAE: {mae}")
print(f"R^2: {r2}")
结果输出如下:
MSE: 1432261.1369255823
RMSE: 1196.7711297176174
MAE: 966.2598697379169
R^2: 0.7227534193597299
解读:MSE、RMSE、MAE(Mean Absolute Error,平均绝对误差)和R²,都在预期的范围内,这表明模型在测试集上的表现是合理的。R²值0.72表示模型能解释目标变量72.3%的方差,这通常被认为是一个相当好的结果。
至此,我们即完成了整个线性回归的机器学习建模流程。
4.5 拓展:线性回归的决定系数
对于线性回归模型来说,除了SSE以外,我们还可使用决定系数(R-square,也被称为拟合优度检验)作为其模型评估指标。决定系数的计算需要使用之前介绍的组间误差平方和和离差平方和的概念。在回归分析中,SSR表示聚类中类似的组间平方和概念,表意为Sum of squares of the regression,由预测数据与标签均值之间差值的平方和计算的出:
S S R = ∑ i = 1 n ( y i ˉ − y i ^ ) 2 SSR =\sum^{n}_{i=1}(\bar{y_i}-\hat{y_i})^2 SSR=i=1∑n(yiˉ−yi^)2
而SST(Total sum of squares)则是实际值和均值之间的差值的平方和计算得到:
S S T = ∑ i = 1 n ( y i ˉ − y i ) 2 SST =\sum^{n}_{i=1}(\bar{y_i}-y_i)^2 SST=i=1∑n(yiˉ−yi)2
并且, S S T SST SST可由 S S R + S S E SSR+SSE SSR+SSE计算得出。而决定系数,则由 S S R SSR SSR和 S S T SST SST共同决定:
R − s q u a r e = S S R S S T = S S T − S S E S S E = 1 − S S E S S T R-square=\frac{SSR}{SST}=\frac{SST-SSE}{SSE}=1-\frac{SSE}{SST} R−square=SSTSSR=SSESST−SSE=1−SSTSSE
决定系数是一个鉴于[0,1]之间的值,并且约趋近于1,模型拟合效果越好。
5. 线性回归模型的应用
5.1 模型的实际应用
在完成模型训练后,将训练好的模型保存到名为"linear_regression_model.pkl"的文件中,并使用pickle模块的dump函数进行保存。然后,我们使用pickle模块的load函数加载模型。接下来,我们使用加载的模型对一个样本进行预测,这里假设我们想预测第一条测试样本的"Production"值。最后,我们打印出预测的"Production"值。
import pickle
# 保存训练好的模型到文件
model_file = 'linear_regression_model.pkl'
with open(model_file, 'wb') as f:
pickle.dump(model, f)
# 加载模型
with open(model_file, 'rb') as f:
loaded_model = pickle.load(f)
# 输入一条样本进行预测
sample = X_test.iloc[0] # 假设你想预测第一条测试样本
prediction = loaded_model.predict([sample])
print(f"Predicted Production: {prediction[0]}")
# 输出如下:
# Predicted Production: 9665.677833927311
请注意,加载模型之前,你需要确保pickle文件和加载模型的代码在同一个目录下,或者提供正确的文件路径。
5.2 如何自定义输入得到预测结果
很多博客在完成上述就结束了,但我们不会这样做。训练模型的目的是为了在现实中使用它。我们需要将模型应用到实际问题中,用它来做出预测。要么如何应用呢?上面我们训练了一个线性回归模型,并希望将其应用于新的数据以进行预测。我们可以创建一个函数,它可以接收新的数据,并返回模型的预测结果。请注意,你需要对新数据进行与训练数据相同的预处理步骤,包括移除离群值、标准化连续变量以及仅保留与目标变量相关性大于阈值的特征。
import pandas as pd
import pickle
from scipy import stats
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
import numpy as np
def preprocess_data(df):
# 将Z分数大于3或小于-3的点视为离群值
z_scores = np.abs(stats.zscore(df._get_numeric_data()))
if (z_scores >= 3).any().any():
print("Warning: The new data contains outliers.")
# 将连续变量进行标准化
scaler = StandardScaler()
continuous_columns = ['Position', 'Angle_of_Installation', 'Device_Orientation', 'Year', 'Device_Capability']
df[continuous_columns] = scaler.fit_transform(df[continuous_columns])
return df
def predict_production(new_data):
# 进行数据预处理
new_data = preprocess_data(new_data)
print()
# 特征选择
new_data = new_data[['Area', 'Position', 'Device_Capability', 'Degree_of_Shading']]
# 加载训练好的模型
with open("linear_regression_model.pkl", 'rb') as f:
loaded_model = pickle.load(f)
# 预测Production
predictions = loaded_model.predict(new_data)
return predictions
# 读取新的CSV文件
new_data = pd.read_csv("predict_data.csv")
# 进行Production预测
predictions = predict_production(new_data)
# 打印预测结果
print(predictions)
代码解读:
上述代码使用训练好的线性回归模型对新的数据进行Production的预测。具体步骤如下:
-
preprocess_data函数用于对数据进行预处理。它首先使用stats.zscore计算数据的Z分数,将Z分数大于3或小于-3的数据点视为离群值,并打印警告信息。然后,使用StandardScaler对连续变量进行标准化,包括’Position’, ‘Angle_of_Installation’, ‘Device_Orientation’, ‘Year’, 'Device_Capability’这些特征。
-
predict_production函数用于进行Production的预测。首先对新的数据进行数据预处理,调用preprocess_data函数进行处理。然后,选择特定的特征’Area’, ‘Position’, ‘Device_Capability’, 'Degree_of_Shading’用于预测。接下来,通过pickle.load从文件中加载训练好的线性回归模型。最后,使用加载的模型对新数据进行预测,得到Production的预测结果。
-
读取新的CSV文件,将数据存储在new_data中。
-
调用predict_production函数对新数据进行Production的预测,将预测结果存储在predictions中。
该方案通过预处理和特征选择来准备新的数据,并利用训练好的模型进行预测,从而得到Production的预测结果。
预测结果如下:
[ 8723.46417964 11946.90624717 8211.40862404 8726.82234903
9090.02956616 13483.74723712 13167.02285596 9566.41311498]
5.2 模型的部署
为了在实际问题中使用模型,需要将模型部署到生产环境中。这个过程可能涉及将模型代码转化为一个可以在生产环境中运行的服务,可能是一个Web服务,也可能是一个嵌入到现有系统中的模块。这部分内容就不在此篇文章中论述了,后面的案例我会做到,感兴趣的朋友可以关注一波
6. 线性回归模型的局限性
6.1 线性关系影响
尽管上述建模过程能够发现,面对白噪声不是很大、并且线性相关性非常明显的数据集,模型整体表现较好,但在实际应用中,大多数数据集可能都不具备明显的线性相关性,并且存在一定的白噪声(数据误差)。此时多元线性回归模型效果会受到极大影响。
import numpy as np
import matplotlib.pyplot as plt
# 生成数据集
np.random.seed(0)
x = np.linspace(-5, 5, 100)
y = x**2 + 1
# 添加噪声
noise = np.random.normal(0, 10, size=x.shape)
y_noisy = y + noise
# 绘制散点图
plt.scatter(x, y_noisy, label='Data with Noise')
# 拟合模型
coefficients = np.polyfit(x, y_noisy, deg=1) # 使用一次多项式拟合数据
y_pred = np.polyval(coefficients, x)
# 绘制模型预测直线
plt.plot(x, y_pred, color='red', label='Model Prediction')
# 设置图例、标题和坐标轴标签
plt.legend()
plt.title('Data with Noise and Model Prediction')
plt.xlabel('x')
plt.ylabel('y')
# 显示图像
plt.show()
在上述示例代码中,首先使用NumPy生成一个包含100个点的x轴数据,然后根据 y = x 2 + 1 y=x^2+1 y=x2+1的规律计算对应的y轴数据。接着使用np.random.normal函数生成服从正态分布的噪声,并将其添加到y轴数据上,得到带有噪声的数据集。然后使用np.polyfit函数拟合一次多项式(即直线)到数据集上,得到模型的参数。最后,使用np.polyval函数根据拟合得到的参数计算模型对应的y轴数据,并将原始数据集和模型预测结果绘制在散点图上。
6.2 最小二乘法条件限制
线性回归模型还面临这一个重大问题就是,如果特征矩阵的交叉乘积不可逆,则最小二乘法求解过程就不成立了。
w ^ = ( X T X ) − 1 X T y \hat w = (X^TX)^{-1}X^Ty w^=(XTX)−1XTy
当使用最小二乘法求解线性回归模型时,需要计算特征矩阵的转置与特征矩阵的乘积。如果特征矩阵的乘积不可逆,意味着特征之间存在高度相关性,或者特征矩阵的维度过大导致特征之间线性相关性较强,这会导致特征矩阵不满秩。
在这种情况下,最小二乘法的求解过程就无法进行,无法得到唯一的最优解。直观地理解,当特征之间高度相关时,模型无法确定每个特征对目标变量的独立贡献,因为它们之间的影响是相互重叠的。另外,当特征矩阵的维度过大时,可能存在冗余的特征或特征之间的线性相关性,这会导致特征矩阵不满秩。
在这种情况下,需要考虑其他的解决方案,例如使用正则化方法(如岭回归、Lasso回归)来处理高度相关的特征或通过特征选择减少冗余的特征。此外,还可以考虑使用其他非线性回归模型来处理特征之间的复杂关系。
总之,特征矩阵的乘积不可逆是最小二乘法在求解线性回归时的一个限制,意味着无法得到唯一的最优解。这时候需要考虑其他方法来解决模型建立的问题。这个后续我们会提出详细的优化方法。
当特征矩阵的乘积不可逆时,可以通过以下表格示例来帮助理解。
| 特征1 | 特征2 | 目标变量 |
|---|---|---|
| 1 | 2 | 5 |
| 2 | 4 | 9 |
| 3 | 6 | 12 |
| 4 | 8 | 17 |
假设上述表格中的特征矩阵为X,目标变量列为y。特征矩阵X的第一列为特征1,第二列为特征2。
使用最小二乘法求解线性回归模型时,需要计算特征矩阵X的转置与X的乘积。但是,当特征矩阵存在线性相关性时,例如第二列的值恰好是第一列的两倍,特征矩阵的乘积将不可逆。
在上述表格中,特征1和特征2之间存在线性相关性。如果尝试计算特征矩阵X的转置与X的乘积,将会得到一个不可逆的矩阵。这意味着最小二乘法无法求解出唯一的最优解。
7. 结语
总结而言,本文档涵盖了线性回归模型的构建与应用的全过程,希望能够帮助读者理解和应用该模型。如果有理论上的不清楚之处,建议参考我们的专栏开篇文章机器学习(一):理解机器学习相关概念进行进一步的学习。
最后,感谢您阅读这篇文章!如果您觉得有所收获,别忘了点赞、收藏并关注我,这是我持续创作的动力。您有任何问题或建议,都可以在评论区留言,我会尽力回答并接受您的反馈。如果您希望了解某个特定主题,也欢迎告诉我,我会乐于创作与之相关的文章。谢谢您的支持,期待与您共同成长!
期待与您在未来的学习中共同成长。