NSGA-II 算法详解

3 NSGA-II

3.1 算法流程

确定种群大小 n，交叉概率 t，迭代次数 g
随机产生 n 个个体，它们整体视为种群 P
for i = 1 to g
      P = ∅ 
      for j = 1 to n
            产生一个 [0,1] 的随机数 a
            if (a<t)
                  从 P 中随机选出两个个体作为父母，交叉产生一
                  个新的个体并放入 P’ 中
            else
                  从 P 中随机选出一个个体，变异产生一个新的个
                  体并放入 P’ 中
            end
      end
      利用非支配排序和拥挤距离，从 P∪P’ 中选出 n 个个体，     代替 P			# NSGA-II改进的部分
end
输出最终种群 P 中的非支配个体

---

3.2 NSGA-II 提出的 NSGA的缺点

• $O(M{N}^3)$计算复杂度(其中M代表目标个数，N代表种群个数)

  NSGA算法每一代进化都要构造非支配集, 在种群规模大的时候会造成巨大的时间开销

• 非精英机制方法

  NSGA算法没有采取保留优秀解的措施, 导致算法性能受损。

• 需要指定共享参数

  指定共享参数是因为NSGA需要依靠共享参数来维持解群体的分布性, 也即实现解尽可能地均匀分布, 但共享参数的定义往往需要一定的经验, 这也导致共享参数的确定成为了老大难的问题。

---

3.3 NSGA-II 较于 NSGA的优点

3.3.1 快速非支配排序

​在NSGA-中，将进化群体按支配时关系分为若干层，第一层为进化群体的非支配个体集合，第二层为在进化群体中去掉第一层个体后所求得的非支配个体集合，第三层为在进化群体中去掉第一层和第二层个体后所求得的非支配个体集合，依此类推。选择操作首先考虑第一层非支配集，按照某种策略从第一层中选取个体;然后再考虑在第二层非支配个体集合中选择个体，依此类推,直至满足新进化群体的大小要求。

1) 论文算法

---

2) 支配关系

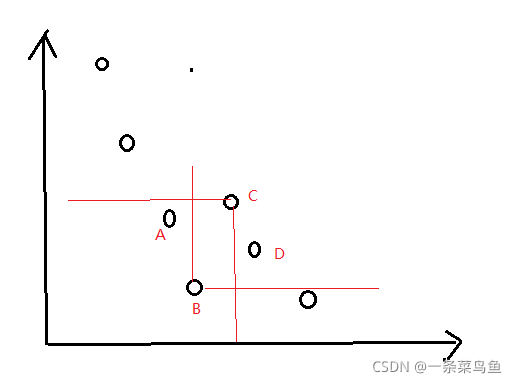
对于二目标优化问题来讲, 支配的含义在于 解A的值在两个目标函数上都优与解B , 这样我们就称 解A支配解B (不理解可以参照 Pareto理论)
假如横纵坐标为两个不同的约束函数, 函数值越小越优秀的情况下。 那么 B 显然能够支配 C和D , 因为 B的两个函数值都小于 C与 D, 因此 $S_p=C,D$ 。 而 C 显然受到 A 和 B 的支配, 因此 $np=2$ 。

---

3) 论文解释

• 原文

  ​ First, for each solution we calculate two entities: 1) domination count $n_p$, the number of solutions which dominate the solution p, and 2) $S_p$, a set of solutions that the solution dominates. This requires $O(M{N}^2)$comparisons.
  ​ All solutions in the first nondominated front will have their domination count as zero. Now, for each solution p with $n_p=0$, we visit each member (q ) of its sets $S_q$ and reduce its domination count by one. In doing so, if for any member q the domination count becomes zero, we put it in a separate list Q. These members belong to the second nondominated front. Now, the above procedure is continued with each member of Q and the third front is identified. This process continues until all fronts are identified.

  ---

• 译文

  ​ 首先，对每一个解我门计算两个实体:1）支配计数$n_p$ ,即支配着解 p 的解的数量，还有 2）$S_p$，解所支配的解的集合，这需要$O(M{N}^2)$次比较。
  ​ 所有第一非支配前沿面解的支配计数都为零。现在，对每一个解 p 都有$n_p=0$，我们访问每一成员(q）和他的集合$S_q$并且减少逐一减少支配计数。通过这样，如果任何成员q的支配计数达到0，我们就把它放进一个单独集合 Q。这些成员属于第二非支配前沿面。现在，以上程序应用 Q中的每一成员继续执行直到第三前沿面被确定。这一过程持续到所有前沿面被确定。

  ---

• 个人理解

  快速非支配排序算法的目的在于将 种群根据相应的支配关系划分为不同级别的Pareto解 , 根据约束函数划分为 $Paret{o}_1、Paret{o}_2......Paret{o}_N$ 等若干个等级。算法首先完成对所有种群最优解的划分, 也即 $Paret{o}_1$ 级解(也即种群的最优解, 其余解按照$1-N$ 优先级依次递减)。其次完成刨去 $Paret{o}_1$ 级解之后解的划分, 根据支配次数的结果 $n_q$ 的大小, 每执行依次递减, 当执行同一批次 $n_q$ 为零时的解划分为同一等级 (Pareto front) , 直到集合为空, 完成种群 N 的划分。

  ---

4) 伪代码

# 以下是 NSGA-II 的伪代码
# 参数说明
# np表示被多少解支配，是一个数目
# Sp表示该解所支配的解的集合,是一个集合
# P表示整个种群
# 对于参数而言, 这里的参数都是一些假参数, 实际设计时, 解应该是一个具有属性地对象

def fast_nondominated_sort(P):
    F = []      # 初始化 F用来存放支配关系的排序结果(分层划分)
    for p in P:     # 遍历整个种群
        Sp = []         # 支配解集合初始化
        np = 0          # 支配解个数初始化
        for q in P:         # 遍历整个种群
            if p > q:           # 如果p支配q,将q添加到 Sp 列表(p被p支配)
                Sp.append(q)
            elif q > p:         # 如果q支配p,则 np + 1
                np += 1
        if np == 0:      # 如果p没有被其它解支配, 将它设为Pareto 1级, 也即非支配解
            p_rank = 1      #p_rank 是解的一个属性, 代表了当前解的 Pareto等级
        	F1.append(p)     # 将非支配解加入p 集合中
    F.append(F1)    # 将Pareto 1级解加入F群体中
    i = 1
    # 下述算法复杂度为 O(MN^2)
    while F[i]:     # 当F 非空
        Q = []          # Q 存放后续的非支配解
        for p in F[i]:      # 遍历Pareto 1级解集合
            for q in Sp:        # 遍历Pareto 1级解的支配解 该集合 = 全集 - Pareto1级解
                nq -= 1             # 消除了 Pareto上层解 对它的支配
                if nq == 0:     # 如果该个体支配计数为0, 代表是非支配解
                    q_rank = i+1    # 设置该解为与 i + 1前沿面 i 初始为 1
                    Q.append(q)     # 将解存放到Q集合中
        F.append(Q)     # 把Q得到的划分好的非支配解排序结果拼接到 F 结果集内部
        i += 1          # 重复循环 知道F[i]为空, 也即遍历完所有的Pareto 1级解

---

3.3.2 拥挤度与拥挤度比较算子

1) 拥挤度计算公式

$I[i+1].m和I[i-1].m分别是解i后一个与前一个解在m函数上的的函数值$

$f_m^{max}和f_m^{min}分别是第m个函数的最大和最小值$
$$I_{distance}=(I[i+1].m-I[i-1].m)/(f_m^{max}-f_m^{min})$$

---

2) 拥挤比较算子

经过前面的快速非支配排序和拥挤度计算之后，种群中的每个个体 $i$ 都拥有两个属性：非支配排序决定的非支配序 $i_{rank}$（级数，即第几级）和拥挤度 $i_d$。依据这两个属性，可以定义拥挤度比较算子：个体i与另一个个体 j 进行比较，只要下面任意一个条件成立，则个体 $i$ 获胜。

① 如果个体 $i$ 所处非支配层优于个体 $j$ 所处的非支配层，即 $i_{rank}<j_{rank}$

​② 如果它们有相同的等级且个体 $i$ 比个体 $j$ 有一个更大的拥挤距离，即 $i_{rank}=j_{rank}$ 且 $i_d>j_d$

第一个条件确保被选择的个体属于较优的非劣等级。第二个条件根据它们的拥挤距离选择由于在同一非劣等级而不分胜负的两个个体中位于较不拥挤区域的个体(有较大的拥挤度 $i_d$ )。胜出的个体进入下一个操作。

---

3.3.3 精英策略

1) 概述

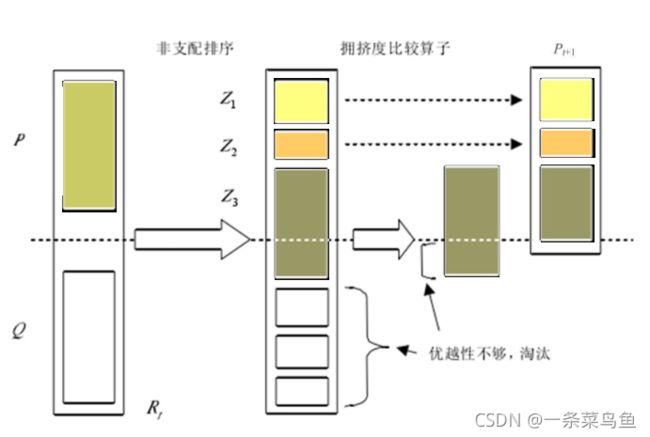
首先将第 t 代产生的新种群 $Q_t$ 与父代 $P_t$ 合并组成 $R_t$ , 种群大小为 $2N$ 。然后 $R_t$ 进行非支配排序产生一系列非支配集 $Z_i$ 并计算拥挤度。由于子代和父代个体都包含在 $R_t$ 中, 则经过非支配排序后的非支配集合 $Z_1$ 是最优的, 所以首先将 $Z_1$ 加入 $P_{t+1}$ 新父代种群中。 如果大小小于 N, 则继续向 $P_{t+1}$ 种群中添加 $Z_2$ 。直到添加 $Z_3$ 时, 种群大小超过了 N , 这时就根据拥挤度比较算子进行选择添加, 使得 $P_{t+1}$ 个体数量达到 $N$。然后通过遗传算子(选择、交叉、变异)产生新的子代种群 $Q_{t+1}$

---

2)主体循环

以上代码的逻辑跟精英策略的逻辑一致。

---

3.4 选择算法

3.4.1 锦标赛选择算法

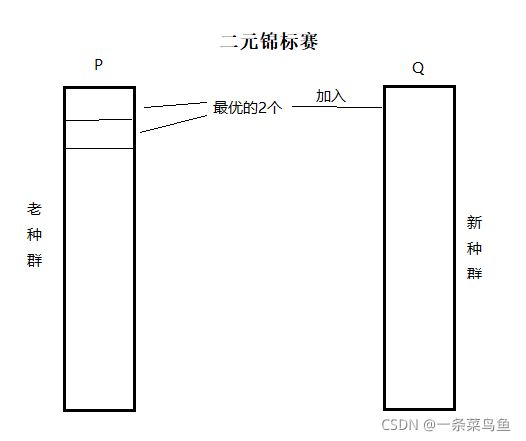
​遗传算法中的锦标赛选择策略每次从种群中取出一定数量个体（放回抽样），然后选择其中最好的一个进入子代种群。重复该操作，直到新的种群规模达到原来的种群规模。几元锦标赛就是一次性在总体中取出几个个体，然后在这些个体中取出最优的个体放入保留到下一代种群的集合中。具体的操作步骤如下：

​① 确定每次选择的个体数量N。（二元锦标赛选择即选择2个个体）
​② 从种群中随机选择N个个体(每个个体被选择的概率相同) ，根据每个个体的适应度值，选择其中适应度值最好的个体进入下一代种群。
​③ 重复步骤②多次（重复次数为种群的大小），直到新的种群规模达到原来的种群规模。