Monocular 3D Object Detection with Depth from Motion 论文学习

论文链接：Monocular 3D Object Detection with Depth from Motion

1. 解决了什么问题？

从单目输入感知 3D 目标对于自动驾驶非常重要，因为单目 3D 的成本要比多传感器的方案低许多。但单目方法很难取得令人满意的效果，因为单张图像并没有提供任何关于深度的信息，该方案实现起来非常困难。

Two view 场景有两个问题：

• 多项预测的错误累积起来，使直接的深度预测变得非常困难；
• 静止状态的相机和运动状态下匹配的模糊性。

2. 提出了什么方法？

受到 3D 目标检测双目方案的启发，本文利用了相机帧间运动（ego-motion）提供的强几何结构关系，进行准确的目标深度估计和检测。其基本原则与双目方法中的深度估计类似。在双目方法中，两个相机被严格约束在同一个平面上，它们之间的距离固定，这个距离就是 baseline。目前的立体 3D 检测方法将该 baseline 作为重要线索，将深度估计问题转换成较容易解决的视差估计问题。类似地，时序上相邻的两帧画面也具有立体匹配关系，但它们的 baseline 是不固定的，依赖于相机的帧间运动。
作者通过具有几何关系的 cost volume 构建立体匹配，作为深度估计的替代方案，用单目理解做进一步的补充，以解决第二个问题。本文提出的 Depth from Motion 使用几何关系将 2D 图像特征提升为 3D 特征， 然后再检测 3D 目标。我们先将复杂的几何关系包含在 cost volume 里面，进行立体估计。为了保证它对任意增广的输入都合理，作者设计了一套流程，在标准空间（即 canonical space）内做姿态变换。此外，作者使用另一个单目 pathway 做补充，用可学习的权重将它们融合起来。

2.1 理论分析

分析了通用的立体深度估计方法。

2.1.1 Object Depth from Binocular Systems

双目方法明确要求两个相机处于同一平面。如下图(a)所示，两个相机的焦距和它们之间的距离（即 baseline）是固定的。根据相机小孔成像模型和相似三角形定理，我们有
$$\frac{d}{f}=\frac{b}{D}\Rightarrow D=f\frac{b}{d}$$

其中$d$是两张图像之间在水平方向的视差，$f$是相机的焦距，$D$是目标的深度，$b$是 baseline。根据上式，目标深度估计可以变换为一个容易解决的视差估计问题。

2.1.2 Object Depth from General Two-View Systems

用双目方法来估计目标的深度，依赖于 two-view 立体几何关系。视频里相邻的两帧也具有类似的立体匹配关系。那么我们能否使用 two-view 几何信息来预测目标的深度？

作者将双目方法的几何关系一步步地扩展到通用的 two-view 场景。假设相机在$t_1$和$t_2$时刻的位置不相同，而且我们知道相机在每个位置的参数。

首先，我们先假设所有的物体是静止的，后面再考虑物体运动的状况。如上图(b)所示，假设相机运动只涉及平移。从相机姿态的变换中可以得到$\Delta x$和$\Delta D$，在这个平行的例子中，two-view 几何关系满足：

$$\frac{u_1-c_u}{f}=\frac{x_1}{D_1},\frac{u_2-c_u}{f}=\frac{x_2}{D_2},\Delta x=x_1-x_2,\Delta D=D_1-D_2$$

$(u_1,v_1)$和$(u_2,v_2)$是两张图像中两个对应的点，$D_1,D_2$是它们的深度值，$x_1,x_2$是它们在 3D 空间$x$轴的位置。于是推导得到：

$$D_1=\frac{f(\Delta x-\frac{u_2-c_u}{f}\Delta D)}{u_1-u_2}\stackrel{\Delta D=0}{}\frac{f\Delta x}{u_1-u_2}$$

双目方法中的几何关系就是其特殊情况，即$\Delta D=0$。

如上式所示，与双目方法不同，这里的 baseline 不再是固定的，而是依赖于相机的自身运动$\Delta x,\Delta D$以及目标的绝对位置$u_2$。因此，目标的深度估计除了依赖于视差$u_1-u_2$，也依赖于这些因素。

为了更好地理解，作者在 KITTI 基准上以双目方法举例，进行定量比较。一个合理的 baseline 不应过大或过小。Baseline 过大会造成两张图像重叠区域很小；baseline 过小会造成视差非常小，深度估计错误就会增大。所以作者以双目 baseline (KITTI 中是$0.54m$)为例，用$\Delta x-\frac{u_2-c_u}{f}\Delta D$得到。因为水平平移距离$\Delta x$通常要远远小于$0.54m$，我们就需要沿着深度方向$(\Delta D)$平移较大的距离，并与 2D 相机中心点保持较远的水平距离$(u_2-c_u)$，从而使 baseline 足够大，适合做立体匹配。例如，为了得到一个$0.54m$的 baseline，当$\Delta D=5.4m,f=700$像素时，我们需要$u_2-c_u=70$。
当$\Delta D=2.7m$时，我们需要$u_2-c_u=140$。这就是说，对于远离中线的物体，估计会更加准确，不然就可能会遇到问题。

有了这些基础，上图 c 在视差计算中，引入了与目标绝对位置有关的旋转系数，而上图(d) 则引入了相对平移和旋转系数。绝对位置和运动估计的误差越多，深度估计就越发困难。

2.1.3 Achilles Heel of Depth from Motion

依据上面的分析，在 two-view 方法中，直接推导深度信息会牵扯到多项估计，如目标的绝对位置和运动，这些错误累积起来会非常棘手。此外，有多个场景是基于立体的方法无法解决的，比如静态相机没有 baseline，匹配低纹理区域存在的模糊性问题。

因此，受到双目方法的启发，作者将复杂的几何关系包含在一个 plane-sweep cost volume 里面，作为立体匹配的替代方案：考虑到我们无法直接从视差估计深度，于是为每个像素点提供候选的深度值，将这些 $2.5D$点反投到另一帧，再根据像素特征的相似度，学习哪一个深度值是最可能的。此外，为了解决第二个问题，作者引入了用于单目理解的 path，弥补立体估计的缺陷。

2.2 方法

3D 目标检测流程通常包含三个阶段：从输入图像提取特征、将特征上升到 3D 空间、最后检测 3D 目标。下图展示了本文的整体架构，提出了两个关键设计：含有几何信息的 cost volume 和用于立体估计的单目补偿。

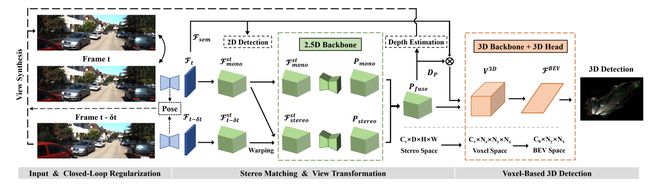
2.2.1 Overview

2D Feature Extraction

受到双目方法启发，给定两张输入图像$(I_t,I_{t-\delta t})$，首先使用 2D 主干网络提取特征$({\mathcal{F}}_t,{\mathcal{F}}_{t-\delta t})$。

2D 主干网络使用的是带空间金字塔池化及特征上采样的 ResNet-34。其上面接着一个小型的 U-Net，将 SPP 特征图上采样至全分辨率。使用两种 necks，一个输出几何特征$F_t$做立体匹配，一个输出语义特征$F_{sem}$。为保证$F_{sem}$能得到正确的监督信号，$F_{sem}$也用于辅助的 2D 检测。

Stereo Matching and View Transformation

用预定义的离散深度层级提升${\mathcal{F}}_t$，得到立体空间的${\mathcal{F}}_{mono}^{st}$，用于后续的单目理解。
得到$({\mathcal{F}}_t,{\mathcal{F}}_{t-\delta t})$之后，我们通过它们之间的姿态变换构建出 stereo cost volume ${\mathcal{F}}_{stereo}^{st}$。用一个 dual-path 3D 聚合网络对这两个 volumes 做过滤，估计深度分布 volume$D_P$。$D_P(u,v,:)$代表了像素$(u,v)$在所有深度层级的分布。使用投影的 LiDAR 点云来监督该深度的预测。

然后用$D_P$来提升语义特征${\mathcal{F}}_{sem}$。再将其和几何立体特征$P_{fuse}$结合，即最终的立体特征，再从其中采样体素特征。如上图所示，这个过程将立体空间的特征变换到体素空间，体素空间结构规整，更适合做目标检测。

Voxel-Based 3D Detection

融合通道维度和高度维度，将 3D 特征$V^{3D}$变换到 BEV 空间，使用 2D hourglass 网络聚合 BEV 特征。最终，用一个轻量的 head 预测 3D 框和类别。训练损失包括两个部分：深度回归损失、2D/3D 检测损失。

2.2.2 Geometry-Aware Stereo Cost Volume Construction

立体匹配的关键部分就是 cost volume。与双目场景不同，两帧之间的姿态变换是刚性的，由平移和旋转组成。这个差异影响了其构建 cost volume，很难对输入数据做增广。

对于立体 volume 的每个位置$\mathbf{x}=(u,v,w)$，我们可以推导出反投影矩阵$\mathcal{W}$，将${\mathcal{F}}_{t-\delta t}$变形（warp）至第$t$帧，然后与相应的特征 concat：

$${\mathcal{F}}_{stereo}^{st}(u_t,v_t,w_t)=\text{concat}\left[{\mathcal{F}}_t(u_t,v_t),{\mathcal{F}}_{t-\delta t}(u_t-\delta t,v_t-\delta t)\right]$$

$$(u_{t-\delta t},v_{t-\delta t},d(w_t-\delta t){)}^T=\mathcal{W}(u_t,v_t,d(w_t){)}^T,\mathcal{W}=KT{K}^{-1}$$

这里$(u_t,v_t,w_t)$和$(u_{t-\delta t},v_{t-\delta t},w_{t-\delta t})$代表两帧的立体空间的像素坐标。计算相应深度的式子是$d(w)=w\cdot \Delta d+d_{min}$，$\Delta d$是划分的深度间隔，$d_{min}$是检测范围内的最小深度值。$\mathcal{W}$是反投影矩阵，将内参矩阵$K$、自车运动（刚性变换）$T$和$K^{-1}$相乘得到，这里假定两帧的内参矩阵相同。作者发现，任意的数据增广，如图像缩放和翻转，都能影响反投矩阵$\mathcal{W}$的合理性。从增广图像构建 geometry-aware stereo cost volume 并不简单。

因此，作者设计了一个方法来解决该问题。如下图(a)，需要在两个增广的图像特征$({\mathcal{F}}_t,{\mathcal{F}}_{t-\delta t})$中找到对应的特征。核心思想就是保证 warp 变换是在 3D 真实世界（即标准空间）中进行。例如，如果我们对输入的两张图片进行翻转、缩放和裁剪操作，首先要将预先定义的深度层级附加到${\mathcal{F}}_t$里每个 2D 网格坐标的后面，将每个$2.5D$坐标提升为$3D$。变换时，通过修改内参矩阵$K$（缩放和裁剪操作等比例对应着相机的焦距和中心点坐标），可以抵消缩放和裁剪造成的影响。然后，翻转立体网格${\tilde{G}}_t^{st}$，得到标准空间的$G_t^{st}$。对新网格做姿态变换，得到$G_{t-\delta t}^{st}$，将它投影到$2D$平面，得到若干个${\tilde{G}}_{t-\delta t}$网格图。最后，再对${\tilde{G}}_{t-\delta t}$做一遍图像增广，就可以采样相应的特征了。

这样，我们就能对输入图像做任意的增强，而不会影响到 ego-motion 变换的内在合理性。

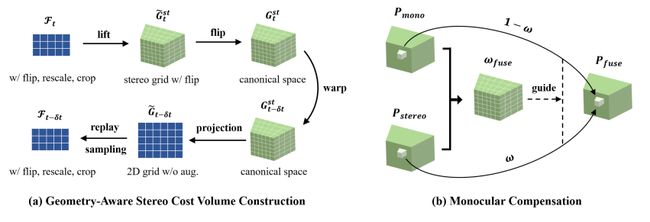
2.2.3 Monocular Compensation

立体深度估计和单目深度估计的底层逻辑是不同的：立体估计依赖于匹配，而单目估计则依赖于数据驱动的先验信息，和对一张图像的语义与几何信息的理解。如上所述，有一些场景是立体估计也无法处理的。因此，作者加入了单目上下文的先验，以补充立体深度估计的缺陷。

如上图(b) 所示，使用了两个 3D hourglass 网络，分别聚合单目和立体特征。这两个 path 的网络有着相同的结构，但${\mathcal{F}}_{mono}^{st}$的输入通道数是${\mathcal{F}}_{stereo}^{st}$的一半。这样在立体空间，我们就有了两个形状一样的特征 volumes $P_{mono}$和$P_{stereo}$。为了聚合这俩特征，作者设计了一个简单而有效的机制。首先，将$P_{mono}$和$P_{stereo}$ concat 起来，输入进一个简单的 2D $1\times 1$卷积网络，沿着深度通道聚合，将通道从$2D$压缩为$D$。然后将该特征输入 sigmoid 函数，得到权重${\omega }_{fuse}$，它指导如何融合$P_{mono}$和$P_{stereo}$。卷积网络记做$\varphi$，计算过程如下：

$${\omega }_{fuse}=\sigma (\varphi (P_{mono},P_{stereo})),P_{fuse}={\omega }_{fuse}\circ P_{stereo}+(1-{\omega }_{fuse})\circ P_{mono}$$

这里$\sigma$表示 sigmoid 函数，$\circ$表示逐元素相乘。将立体特征$P_{fuse}$输入 softmax 函数，然后直接用于预测深度分布，再输入进后续网络做 3D 检测。

这个设计简洁、高效。图像上每个位置的权重分布都由单目和立体的深度分布得到。可以通过可视化${\omega }_{fuse}$权重，来验证本方法的有效性。

2.2.4 Pose-Free Depth from Motion

这样我们就有了一个统一的架构，从连续帧进行深度估计并检测 3D 物体了。在双目场景中，自车姿态（如 baseline）是一个重要信息。给定姿态变换，我们就能估计出深度信息。尽管在实际使用时很容易获取姿态，作者仍提供了一个无需姿态的方案。这对移动设备很重要。

学习姿态的关键在于目标的表达形式。任意刚性姿态变换都可解耦成平移和旋转，各自有三个自由度。以前的工作通常是回归三维平移量和三个欧拉角。回归平移量$t$很直接。对于旋转角度的回归，则使用了一个单位四元组$\mathbf{q}$来表示旋转角度目标。

姿态解码器网络的输出是一个七维向量，包括三维平移量和四维未归一化的四元组。解码器包括一个 bottleneck 层和三个卷积层。基线模型用 L1 损失进一步监督输出：

L t = ∥ t − t ^ ∥ 1 , L r = ∥ q − q ^ ∥ q ^ ∥ ∥ 1 , L p o s e = L t + λ r L r \mathcal{L}_{t}=\left\|\mathbf{t-\hat{t}}\right\|_1,\quad\quad \mathcal{L}_r=\left\|\mathbf{q-\frac{\hat{q}}{\left\|\hat{q}\right\|}}\right\|_1,\quad\quad \mathcal{L}_{pose}=\mathcal{L}_t+\lambda_r \mathcal{L}_r Lt​= ​t−t^ ​1​,Lr​= ​q−∥q^​∥q^​​ ​1​,Lpose​=Lt​+λr​Lr​
这个损失有多个问题：

• 需要对不同的场景调整权重${\lambda }_r$，代价比较高；
• 用两张图片直接回归 3D eog-motion 有域差异问题；
• 训练时仍然需要姿态标注信息，并非完全不需要姿态信息。

因此，作者使用了一个自监督损失。该损失包括一个外观匹配损失${\mathcal{L}}_p$和深度平滑损失${\mathcal{L}}_s$：
$${\mathcal{L}}_{pose}(I_t,I_{t-\delta t})={\mathcal{L}}_p(I_t,I_{t-\delta t\to t})+{\lambda }_s{\mathcal{L}}_s$$

这里$I_{t-\delta t\to t}$表示第$t$帧合成了第$t-\delta t$帧的图像、深度和预测的姿态。 ${\mathcal{L}}_p,{\mathcal{L}}_s$定义如下：

$${\mathcal{L}}_p(I_t,I_{t-\delta t\to t})=\frac{\alpha }{2}(1-\text{SSIM}(I_t,I_{t-\delta t\to t}))+(1-\alpha )\Vert I_t-I_{t-\delta t\to t}\Vert$$
$${\mathcal{L}}_s({\hat{D}}_t)=|{\delta }_x{\hat{D}}_t|e^{-|{\delta }_x{I}_t|}+|{\delta }_y{\hat{D}}_t|e^{-|{\delta }_y{I}_t|}$$

${\mathcal{L}}_p$是用 Structural Similarity (SSIM) 项和 L1 损失项构成。${\mathcal{L}}_s$在低纹理梯度区域（${\delta }_x,{\delta }_y$值较小），用于正则化预测深度图${\hat{D}}_t$。作者使用了激光雷达信号来监督深度值的学习，而只用了自监督损失来学习姿态。由于是用绝对深度值来监督学习深度信息，我们就能够得到姿态信息，即便没有姿态的标注。