Bridging the Gap Between Anchor-based and Anchor-free Detection via ATSS 论文学习

1. 解决了什么问题？

Anchor-based 和 anchor-free 方法的本质差异其实是如何定义正负样本，如果训练过程中它们采用相同的正负样本定义，最终的表现是差不多的。也就是说，如何选取正负样本才是最重要的。

以单阶段 anchor-based 方法 RetinaNet 和基于中心点的 anchor-free 检测器 FCOS 为例，二者有以下三方面的差异：

• 每个位置上 anchor 的个数：RetinaNet 在每个位置上有多个 anchor boxes，而 FCOS 在每个位置上只有一个 anchor point；
• 正负样本定义：RetinaNet 使用 IoU 来判定正负样本，而 FCOS 使用空间和尺度约束来选择样本；
• 回归的起始状态：RetinaNet 是从预设的 anchor box 回归目标框，而 FCOS 是从 anchor point 定位目标。

作者从上面三个方面出发，分析为什么 FCOS 的表现优于 RetinaNet。此外，通过一系列实验表明，发现在一个位置放置多个 anchors 来检测物体并不是必要的。

2. 提出了什么方法？

提出了一个自适应的训练样本选取方法，根据目标的统计特征自动选取正负样本，将 anchor-based 方法和 anchor-free 方法对齐。

2.1 Anchor-based 和 anchor-free 检测的差异分析

不失一般性，作者采用 RetinaNet 和 FCOS 进行比较，分析其差异。主要关注三个差异：正负样本定义、回归的初始状态和每个位置的 anchors 个数。

2.1.1 实验设定

数据集

全部实验采用 MS COCO，包含80个类别。

训练细节

使用在 ImageNet 上预训练的 ResNet-50 网络，主干网络包括 5 个特征金字塔层级。对于 RetinaNet，5-层特征金字塔的每一层都关联一个正方形 anchor，其大小是$8S$，$S$是总步长。训练时，缩放输入图像，保证其短边长度为$800$，长边长度$\le 1333$。使用 SGD 算法训练$90K$次，momentum 为$0.9$，weight decay 为$0.0001$，batch size 是$16$。初始学习率为$0.01$，在第$60K$次和$80K$次时，学习率除以$10$。

推理细节

如训练过程一样，缩放图像的大小，输入网络，输出预测框和类别。用阈值$0.05$过滤掉背景框，然后每个金字塔输出前$1000$个检测结果。最后使用 NMS，每个类别的 IoU 阈值为$0.6$，每张图片输出前$100$个检测置信度最高的结果。

2.1.2 Inconsistency Removal

每个位置只有一个正方形 anchor box 的 RetinaNet 记做 RetinaNet(#A=1)，从而与 FCOS 保持一致。但是在 MS COCO 上，FCOS 的$37.1\%$领先 RetinaNet(#A=1) 的$32.5\%$很多。若 FCOS 使用一些新的改进，如将 center-ness 移到回归分支、GIoU 损失、用步长归一化回归目标等 tricks，可将其 mAP 从$37.1\%$进一步扩大至$37.8\%$。FCOS 里面使用的一些通用的方法：

• 在 heads 中使用 GroupNorm，
• 回归损失使用 GIoU，
• 将正样本约束在 ground-truth 框内，
• 增加 center-ness 分支，
• 给特征金字塔的每一层添加一个可训练的标量参数等。

这些方法也可加入到 anchor-based 检测器中，因此它们并不是 anchor-based 和 anchor-free 方法的本质差异。如下表，作者挨个地将这些 tricks 应用到 RetinaNet(#A=1)，从而保持一致。这些技巧能将 RetinaNet 提升到$37.0\%$，但与 FCOS 仍有$0.8\%$的差距。

2.1.3 Essential Difference

排除了上述因素后，FCOS 和 RetinaNet(#A=1) 只剩下两点区别。一个是分类子任务，即如何定义正负样本。另一个是回归子任务，即是从 anchor box 还是 anchor point 开始回归。

分类

RetinaNet 使用 IoU 将不同金字塔层级的 anchor boxes 划分为正样本和负样本。它首先将每个目标最优的 anchor box 和$IoU>{\theta }_p$的 anchor box 列为正样本，将$IoU<{\theta }_n$的 anchor boxes 列为负样本，其余的在训练中被忽略。FCOS 使用空间约束和尺度约束划分不同金字塔层级的 anchor points。它首先将 ground-truth 框内的 anchor points 当作候选正样本，然后根据金字塔每一层的尺度范围选出最终的正样本，未被选中的 anchor points 作为负样本。

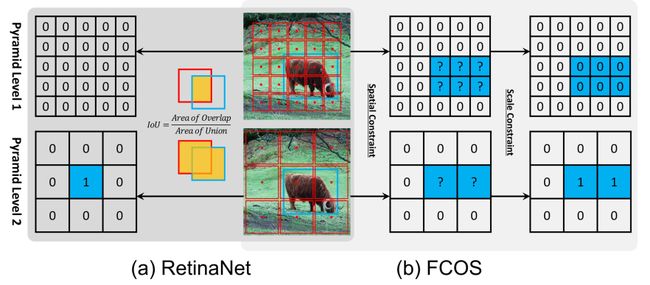
FCOS 先用空间约束在空间维度中找寻候选正样本，然后在尺度维度中使用尺度约束选取最终的正样本。而 RetinaNet 通过 IoU 同时在空间和尺度维度，直接选取最终的正样本。这两种样本选取策略会产生不同的正负样本。RetinaNet 使用了空间和尺度约束策略后，其 AP 从$37.0\%$提升到了$37.8\%$。而 FCOS 使用了 IoU 策略后，其 AP 则降低到了$36.9\%$。这说明如何定义正负样本的才是 anchor-based 和 anchor-free 的关键差异。

回归

有了正负样本后，我们用正样本来回归目标的位置。上图，红点和红框表示 anchors，蓝点和蓝框表示目标中心和目标框。RetinaNet 回归 anchor box 到目标框的四个偏移量，而 FCOS 则回归 anchor point 到边框四条边的四个距离。RetinaNet 回归的初始状态是一个边框，而 FCOS 是一个点。但是从上表可以看出，当 RetinaNet 和 FCOS 采用了相同的样本选取策略，得到一致的正负样本，最终表现没有明显差异。这说明初始回归状态并不重要。

结论

单阶段 anchor-based 和 center-based 检测器的核心差异就是如何定义正负样本的。

2.2 Adaptive Training Sample Selection

训练一个目标检测器时，首先需要为分类任务定义正负样本，然后使用正样本来回归。根据前面分析，分类任务更加重要，FCOS 就改进了这一任务。FCOS 引入了一个新的定义正负样本的方法，效果要比 anchor-based 的 IoU 策略好。于是，下面探讨一个问题：如何定义正负样本。

2.2.1 Description

以前的样本选取策略都涉及一些超参数，如 anchor-based 检测器里的 IoU 阈值和 anchor-free 检测器的尺度范围。Ground truth 边框必须根据这些固定规则来选取正样本，这对一些离群目标不友好。因此，不同的超参设定会得到不同的结果。

于是作者提出了 ATSS，根据目标的统计特征自动地划分正负样本。Algorithm 1 介绍了该方法。对于图像中每个 ground-truth $g$，首先找到它的候选正样本。在每个金字塔层级上根据 $L2$ 距离，选取距离$g$中心点最近的$k$个 anchor boxes。假设特征金字塔有$\mathcal{L}$个层级，ground-truth 框$g$就有$k\times \mathcal{L}$个候选正样本。计算这些候选样本和$g$的 IoU，记做${\mathcal{D}}_g$，其均值和标准方差是$m_g,v_g$。然后，ground-truth $g$的 IoU 阈值就是$t_g=m_g+v_g$。最后，选取$IoU\ge t_g$的候选样本为正样本。我们也将正样本的中心点约束在 ground-truth 框内。如果一个 anchor box 被分给多个 ground-truth 框，选取 IoU 最高的那个 ground-truth 框，其余的作为负样本。

根据 anchor box 和目标的中心点距离选取候选样本。在 RetinaNet，当 anchor box 的中心离目标框的中心越近，IoU 就越大。在 FCOS，距离目标中心点越近的 anchor point 输出的检测质量就越高。因此，距离目标中心越近的 anchor，该候选样本的质量就越高。

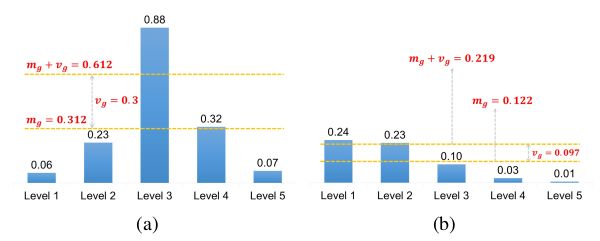
使用均值和标准方差的和作为 IoU 阈值。IoU 均值$m_g$衡量预设 anchors 对当前目标的适合程度。$m_g$的值越大表示该目标的候选样本质量都较高，IoU 阈值就应该设大一些；反之，就该设小一些。IoU 标准方差$v_g$表示哪一层适合检测该目标。$v_g$高说明金字塔有一层特别适合检测该目标，$v_g+m_g$阈值就较大，从而只从那一层选取正样本。而$v_g$值偏小说明金字塔中有多个层适合检测该目标，$v_g+m_g$阈值就较小，就从多个层级中选择合适的样本。将$v_g+m_g$的值设为 IoU 阈值$t_g$，能为每个目标自适应地选择足够多的正样本。

约束正样本的中心点在目标框内。候选框的中心点在目标框以外是不行的，它会利用目标框以外的特征做预测，因此应被排除。
维持不同目标的公平性。理论上，约$16\%$的样本位于置信度区间$\left[m_g+v_g,1\right]$。虽然候选样本的 IoU 并不是标准的高斯分布，但统计结果显示每个目标框会有$0.2\ast k\mathcal{L}$个正样本，这不会随着大小、宽高比和位置而变化。相反，使用了 RetinaNet 和 FCOS 的策略，大目标会有更多的正样本，这就造成了目标之间的不均衡。

几乎没有超参数。本方法只有一个超参数$k$。实验证明模型对$k$值的变化不敏感，ATSS 可以看作没有超参数。