机器学习（14）--XGBoost
目录
一、概述
二、CART、GB、GBDT
1、CART
2、BT（Boosting Tree提升树）
3、GBDT（梯度提升树）
4、GBDT在sklearn中的损失函数
三、Sklearn中的GBDT
1、加载模块
2、划分数据集
3、建模
4、与随机森林和线性回归对比
5、绘制学习曲线
6、n_estimators调参
7、偏差-方差困境
8、subsample
9、eta
四、GBDT的小结
五、XGBoost
1、XGBoost的弱评估器
2、XGBoost目标函数
3、目标函数的不同损失函数
4、深究目标函数
5、分枝策略：贪婪算法
一、概述
XGBoost（eXtreme Gradient BoosTing）是极度梯度提升树，他的基础是梯度提升树（GBDT）。XGBoost作为集成算法中提升法（boosting）的代表算法，相比于单个模型，在分类和回归算法有很优秀的效果表现。
XGBoost的背后也是CART决策树，意味着XGBoost作为一个树模型，也是一个二叉树，只是一次性建立多个平行独立的树，类似于随机森林，但又不同。XGBoost的建模过程：最先建立一棵树，然后根据这一棵树，建立新的一颗树；再根据这两棵树，建立新的一棵树；每次迭代过程中只增加一棵树（弱评估器），逐渐形成一个具有众多树模型的强评估器。
二、CART、GB、GBDT
1、CART
决策树：决策树有三个基本的算法：ID3，C4.5，CART。其中CART是一种基于二叉树的机器学习算法，相比于ID3、C4.5只能用于离散型数据且只能用于分类数据，CART可以处理回归和分类两类问题问题，是所有复杂的决策树，有关决策树的算法的基础。
CART（Classification and Regression Tree）：是一种二元分类和回归树模型。它采用了基尼指数作为分类依据，并且能够处理连续型和离散型数据。CART可以作为回归树也可以作为分类树，这由目标任务所决定。如果是分类树，则采用基尼系数来作为结点分裂依据，如果是回归树，则采用MSE（均方误差）作为结点分裂依据。
基尼系数计算公式：
公式基于分类问题，其中，假设有k个类别，第k个类别的概率为
。其中基尼系数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。
CART分类树原理：
假设m个样本的连续特征A为m个，从小到大进行排列为
，取相邻两个样本值的平均数，一共会取得m-1个点
，其中第i个划分点表示为
,对于这m-1个点，分别计算他们的基尼系数。选择其中基尼系数最小的点作为连续特征进行二元离散分类的点。若取得的基尼系数最小的点为
，则小于
的值为类别0，大于的值为类别1，做到了连续数据进行离散化。
CART回归树原理：
假设有n个训练样本，损失函数定义为MSE。这n个样本首先都在根节点，此时该结点的样本预测值都为节点的训练均值，所以此时的损失值为：
![L=\frac{[(y_1-\bar{y})^2+...+(y_n-\bar{y})^2]}{n}](http://img.e-com-net.com/image/info8/fc9324bdb8b24ae39c2a81bb640ded7d.png){kind=small}
然后，遍历每一个树，在特征中找到一个划分点，让大于和小于该值的样本分别进入左右两个子节点，使得左右两个节点损失值之和最小，然后不断进行递归，直到达到预设条件为止，如最大深度max_depth。
2、BT（Boosting Tree提升树）
提升树算法：
（1）初始化
（2）令
(a)计算残差
(b)拟合残差，生成一个回归树，得到
(c)更新
（3）得到回归问题提升树 
3、GBDT（梯度提升树）
在BT基础上优化了残差的计算方法，使用牛顿法来计算，将残差替代为梯度。GBDT中所有的树必须是回归树，不是分类树。
GBDT算法：
（1）初始化弱学习器
（损失函数默认为均方误差）
（2）令
（a）对每个样本
,计算负梯度，即残差（与BT的区别）
![r_{im}=-[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)}](http://img.e-com-net.com/image/info8/15c13ad636234fac8670719a92bf8b7b.png){kind=small}
（b）将上步的残差作为样本的新真实值，并将数据
作为下一棵i+1树的训练数据（即1到i树的数据和残差），得到一颗新的回归树
，回归树对应的叶子结点区域为
。其中J为回归树t的叶子结点的个数。
（c）对叶子区域计算最佳拟合值
(d)更新强学习器
(3)得到最终学习器
4、GBDT在sklearn中的损失函数
在梯度提升回归树中有四种损失函数：平方损失“ls”，绝对损失“lad”，huber损失“huber”，分位数损失“quantile”，在梯度提升分类树中有两种损失函数：指数损失“exponential”，对数损失“deviance”。梯度下降就是向着负梯度的方向移动，可以求得最小值。
平方损失：
负梯度就是残差。
绝对损失：
负梯度： 
huber损失：
负梯度：
分位数损失：
负梯度：
三、Sklearn中的GBDT
1、加载模块
from xgboost import XGBRegressor as XGBR #xgboost
from sklearn.ensemble import RandomForestRegressor as RFR #随机森林
from sklearn.linear_model import LinearRegression as LinearR #线性回归
from sklearn.datasets import load_boston #波士顿房价数据集
from sklearn.model_selection import KFold,cross_val_score,train_test_split
from sklearn.metrics import mean_squared_error as MSE #均方误差
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt2、划分数据集
data=load_boston()
x=data.data
y=data.target
print(x.shape) #(506,13) 13个特征
xtrain,xtest,ytrain,ytest=train_test_split(x,y,test_size=0.3,random_state=420) #按7:3划分数据集3、建模
reg=XGBR(n_estimators=100).fit(xtrain,ytrain)
print(reg.predict(xtest)) #输出y_pred
print(reg.score(xtest,ytest)) #返回R方，R方越接近1越好
print(MSE(ytest,reg.predict(xtest))) #均方误差
print(reg.feature_importances_) #返回不同特征的重要性分数4、与随机森林和线性回归对比
xgbr_score=cross_val_score(reg,xtrain,ytrain,cv=5).mean() #5折交叉验证,查看训练效果,与模型score接口相同，返回R方
rfr=RFR(n_estimators=100,random_state=420)
rfr_score=cross_val_score(rfr,xtrain,ytrain,cv=5).mean()
lnr=LinearR()
lnr_score=cross_val_score(lnr,xtrain,ytrain,cv=5).mean()
print("XGBR_cross_val_score:",xgbr_score)
print("RFR_cross_val_score:",rfr_score)
print("LinearR_cross_val_score:",lnr_score)XGBR_cross_val_score: 0.799506
RFR_cross_val_score: 0.798916
LinearR_cross_val_score: 0.683507
可见xgboost的交叉验证分数最高，由于波士顿房价数据集还是一个线性数据集，所以分数没有骤降，但相比集成算法xgboost和随机森林还是要低。
5、绘制学习曲线
def plot_learning_curve(estimator,title,x,y,
ax=None,
ylim=None,
cv=None,
n_jobs=None):
from sklearn.model_selection import learning_curve
train_sizes,train_scores,test_scores=learning_curve(estimator,x,y,
shuffle=True,
cv=cv,
random_state=420,
n_jobs=n_jobs)
if ax==None: #没有建立子图，会建立一个子图
ax=plt.gca()
else:
ax = plt.figure() #否则构建坐标轴
ax.set_title(title) #标题
if ylim is not None:
ax.set_ylim(*ylim)
ax.set_xlabel("Train examples")
ax.set_ylabel("Score")
ax.grid()
ax.plot(train_sizes,np.mean(train_scores,axis=1),'o-',
color='r',label='Training score')
ax.plot(train_sizes,np.mean(test_scores,axis=1),'o-',
color='g',label='Test score')
ax.legend(loc='best') #打标签
return ax
cv=KFold(n_splits=5,shuffle=True,random_state=420) #cv必须进行定义类，而不是数字
plot_learning_curve(XGBR(n_estimators=100,random_state=420),title="XGB",x=xtrain,y=ytrain,ax=None,cv=cv)
plt.show()从绘制图像可以看出，训练集学习曲线明显过拟合，测试集学习曲线 不能逼近训练集学习曲线。由于训练集上表现模型学习能力，测试集表现模型泛化能力,则模型仍具有一定的学习能力，可以通过降低训练集学习能力或使得测试集学习曲线与训练集学习曲线相逼近来提高模型效果。
6、n_estimators调参
由于不考虑偏差-方差困境问题，很容易导致n_estimators选择过于大，在测试中输出交叉验证最优时参数为260。
axisx=range(10,1010,50) #从10-1010范围内绘制n_estimators为变量的学习曲线
rs=[]
for i in axisx:
reg=XGBR(n_estimators=i,random_state=420)
rs.append(cross_val_score(reg,xtrain,ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c='r',label='XGB')
plt.legend()
plt.show() 但是，在绘制学习曲线时，很明显发现在150以后基本已经收敛，而过大的n_estimators，也就是xgboost中二叉树的个数，会严重拖慢训练速度，而此时基本能够保证精度的要求，所以进行剪枝。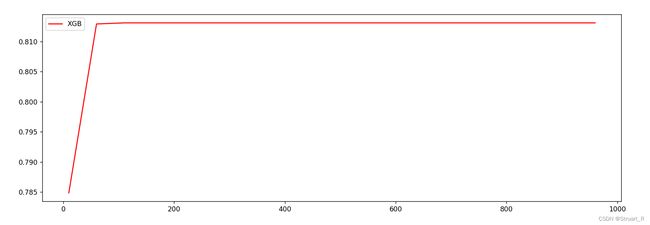 
7、偏差-方差困境
rs=[]
var=[]
ge=[]
for i in axisx:
reg=XGBR(n_estimators=i,random_state=420)
cvs=cross_val_score(reg, xtrain, ytrain, cv=cv)
rs.append(cvs.mean())
var.append(cvs.var())
ge.append((1-cvs.mean()**2)+cvs.var())
print(axisx[rs.index(max(rs))],var[rs.index(max(rs))],max(rs))
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c='r',label='XGB')
plt.legend()
plt.show()输出如下，难道这个和最开始没用偏差方差的分数竟然是一样的！？第二行一般来说方差会出现较小的n_estimator。
260 0.008852347181932483 0.8131149348490775
10 0.7848413102530744 0.005805538902618695
260 0.8131149348490775 0.008852347181932483 0.347696449907312978、subsample
subsample是建模时的一个参数，表示随机抽样时抽取的样本比例，范围（0，1]，默认时为1，表示不进行放回抽样。
对于样本量过少且过拟合的样本，其实进行有放回抽样会带来训练集的学习效果较低，泛化能力也得不到提升。对于样本量庞大的样本，可以进行有放回抽样，一方面可以降低模型训练的时间，另一方面可以提高泛化能力，提升模型效果。
本节基于波士顿房价数据集进行测试subsample的参数效果，由于样本量少，难以提升模型效果。
9、eta
eta表示学习率，与逻辑回归中的α学习率相类比，梯度提升树中使用学习率η迭代集成算法：（在进行k+1次迭代后，k棵树的集成结果
加上新建的树的叶子权重
，等于k+1棵树的预测结果
，不断迭代这个过程，直到找到损失函数最小的
，这个就是模型预测结果）
η越大，迭代速度越快，越有可能出现过拟合，无法收敛到最佳结果，η越小，迭代速度越慢越容易欠拟合，训练时间过长。
计算不用学习率训练下的R2和MSE，可以看到0.2左右的模型效果更好，相比于学习率默认1下。
for i in [0,0.2,0.5,1]: #不同学习率下的r2和MSE
reg=XGBR(n_estimators=100,random_state=420,learning_rate=i).fit(xtrain,ytrain)
print(f"lr={i}")
print(f"r2={reg.score(xtest,ytest)}")
print(f"MSE={MSE(ytest,reg.predict(xtest))}")lr=0
r2=-5.181397220104724
MSE=575.2030263157894
lr=0.2
r2=0.9079161159888034
MSE=8.568763156957433
lr=0.5
r2=0.8825918771246555
MSE=10.925281968986637
lr=1
r2=0.8152271360458629
MSE=17.193832841186456
四、GBDT的小结
对于梯度提升树而言，基本是由三个重要的部分组成：
（1）一个能够衡量集成算法效果的，能够被最优化的目标损失函数Obj
（2）一个能够实现预测的弱评估器
（3）一种能够让弱评估器集成的手段，包括我们讲解的迭代方法，抽样手段，样本加权等过程
XGBoost只需要在GBDT的这三个重要部分中改进，重新定义了损失函数，弱评估器，并且对提升算法的集成进行了改进，实现了运算速度和模型效果的高度平衡。
五、XGBoost
1、XGBoost的弱评估器
在xgboost.XGBRegressor中对于弱评估器参数为booster，可以输入gbree，gblinear或dart。gbtree代表梯度提升树，dart（Dropouts meet Multiple Additive Regression Trees）表示抛弃提升树，可以在建立树时抛弃一部分树，比梯度提升树有更好的防止过拟合的功能。gblinear应用于线性数据。
在sklearn中用不同的弱评估器比较其R2。由于波士顿房价不是所有的特征都是线性的，所以不完全是一个线性数据集，在gblinear下效果不佳。
for booster in ['gbtree','gblinear','dart']:
reg=XGBR(n_estimators=260,learning_rate=0.1,random_state=420,booster=booster).fit(xtrain,ytrain)
print(f"booster: {booster},r2: {reg.score(xtest,ytest)}")booster: gbtree,r2: 0.9262200340627753
booster: gblinear,r2: 0.670622690237168
booster: dart,r2: 0.92622005568523492、XGBoost目标函数
XGBoost的目标函数被写为：传统的损失函数+模型复杂度，相对比其他模型，这样的目标函数更加能衡量模型表现和运算速度的平衡。
目标函数计算公式：
公式中i代表数据集中第i个样本，m表示第k棵树的数据总量，K代表所有的树，也就是n_estimators，第一项代表传统的损失函数，衡量真实标签
与预测标签
之间的差异，通常是RMSE，均方根误差或标准误差。 （下面为MSE和RMSE公式的对比）
第二项代表模型复杂度，使用树模型的某种变换Ω表示，可以代表树模型的复杂度。也为树的特征中已经包含了特征矩阵
,或者说，每一棵树的特征都是前面若干棵树特征与新树叶子权重的融合，而前面若干棵树已经包含了数据 的特征矩阵。
另外，从式子表面而言，第一项与前面K棵树仿佛无关，而第二项式子与K棵树有关，其实不然，在第一项中的已经与K棵树有关，包含了K棵树的迭代效果。
在XGBoost目标函数中其实也蕴含了方差-偏差困境的问题，第一项衡量偏差，模型越坏，第一项越大，第二项衡量方差，模型越复杂，树越多，模型越具体，在不同数据集上的差异会更加巨大，方差越大，所以我们取得Obj的最小值，也就是方差和偏差的平衡点，以求泛化误差最小，运行速度最快。
3、目标函数的不同损失函数
在xgboost.XGBRegressor和xgboost.XGBClassfier中objective参数为目标函数的损失函数。
其中XGB回归器默认使用reg:linear，XGB分类器默认使用binary:logistic。
常见的损失函数：
| 输入 | 损失函数 | 应用 |
| reg:linear | 线性回归，损失函数使用均方误差 | 回归 |
| binary:logistic | 逻辑回归，损失函数使用对数损失 | 二分类 |
| binary:hinge | 支持向量机，损失函数使用Hinge Loss | 二分类 |
| multi:softmax | 使用softmax损失函数 | 多分类 |
4、深究目标函数
下面为对该式子的处理：
注意gi和hi为损失函数对于某一样本的一阶导数和二阶导数，而不是目标函数对某一样本。
作为模型的复杂度等于
，复杂度与叶子的数量深度有关，叶子数量越多，深度越深，复杂度越大，Regularzation表示正则化。
使用L1正则化：
使用L2正则化：
也可以一起使用加大正则化的力度，λ和α都为0时目标函数就是普通的GBDT目标函数。
将所有的式子转换为仅与T（叶子）有关
由于
，
为叶子结点的预测分数，进行如下转换：
最后对
求偏导，令偏导数为0，求解函数极值所对应的，带入原目标函数中。可以看到目标函数基于每一个叶子结点，分数越低，树的整体结构越好，模型效果越好。
5、分枝策略：贪婪算法
在XGBoost中首先使用目标函数来衡量树结构的优劣，然后当树每一次分枝时，计算分枝前的结构分数（就是目标函数）与分枝后的结构分数之差，成为Gain，选择Gain最大的特征上的分枝点进行分枝，当Gain小于某个值时，树停止生长。（可以通过参数控制，类似于决策树的信息熵限制树的分枝）
参考视频：11 4.1 XGBoost应用 (1)：减轻过拟合：XGBoost中的剪枝参数_哔哩哔哩_bilibili
参考文献：《机器学习》周志华